最適化理論/ゲーム理論
提供: Internet Web School
| 1 行: | 1 行: | ||
| - | <math>P,Q</math> | + | <math>P,Q</math>の2人がじゃんけんをする。\\ |
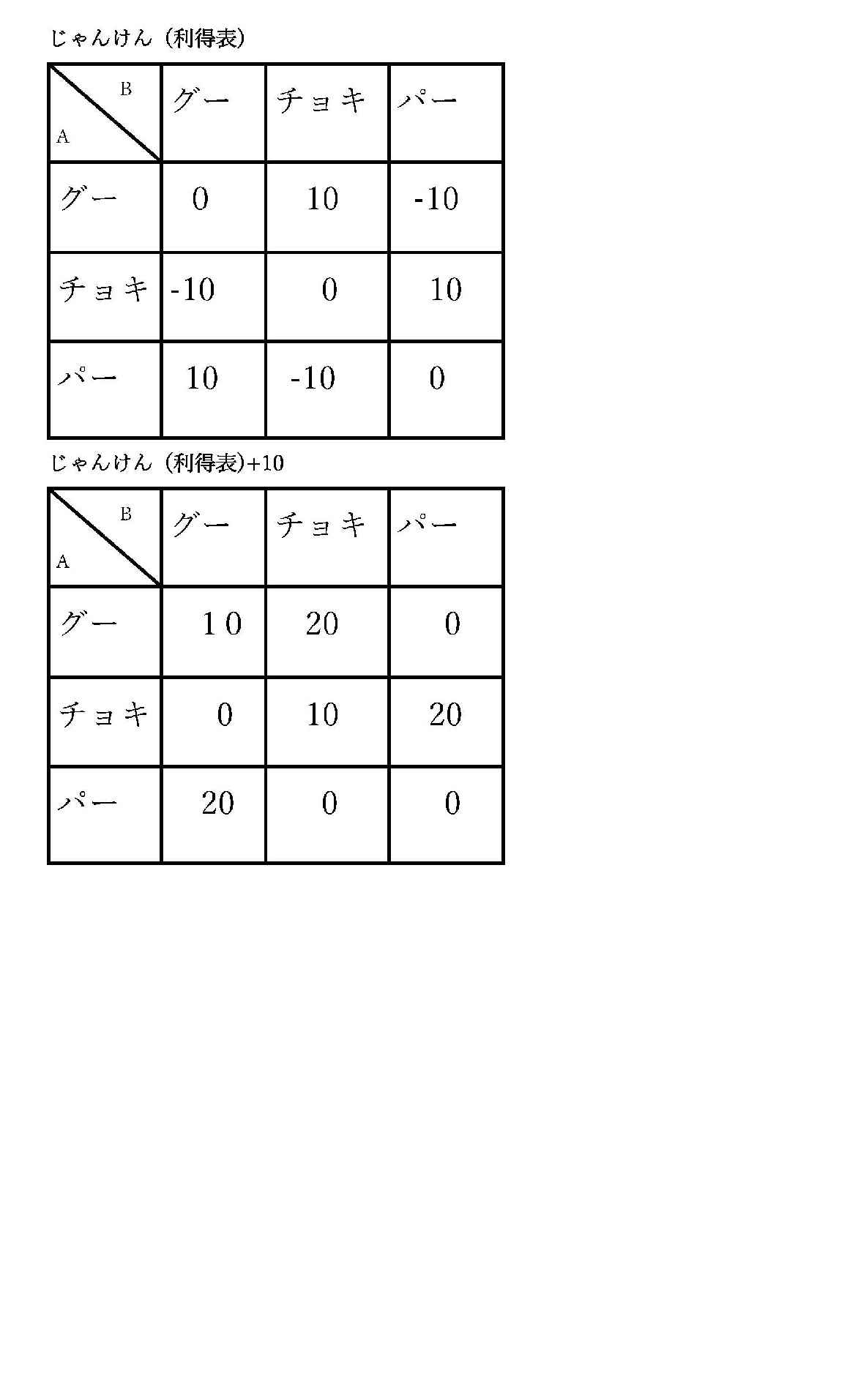
負けたら10円を相手に払い,勝ったら相手から10円貰うというルールで, | 負けたら10円を相手に払い,勝ったら相手から10円貰うというルールで, | ||
じゃんけんを繰り返す。\\ | じゃんけんを繰り返す。\\ | ||
無論,「アイコ」の場合は,支払うお金,貰うお金とも0円である。\\ | 無論,「アイコ」の場合は,支払うお金,貰うお金とも0円である。\\ | ||
| + | <math>P</math>と<math>Q</math>の出す手によって,貰えるお金,支払うお金がどうなるか, | ||
| + | <math>P</math>の立場で以下のように | ||
| + | |||
| + | |||
| + | [[ファイル:Game_ページ_1.jpg]] | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
「-10」は<math>Q</math>に10円払う事を表す。\\ | 「-10」は<math>Q</math>に10円払う事を表す。\\ | ||
| - | <math>P</math>の立場に立ってみます。先ず, | + | <math>P</math>の立場に立ってみます。先ず,このゲームの利得表には鞍点がない。 |
| - | じゃんけんを繰り返すわけであるが, | + | 双方が選択の余地のない「平衡状態」にする戦略はないわけである。出す手をランダムしてゲームを繰り返す方法以外ない。 |
| + | このような問題を混合戦略問題といいます。 \\ | ||
| + | じゃんけんを繰り返すわけであるが,どのような「戦略」があるか?\\ | ||
| 49 行: | 35 行: | ||
| - | ゲームの理論を創始し,この種の問題に解を与えたのが,ノイマン( | + | ゲームの理論を創始し,この種の問題に解を与えたのが,ノイマン(<math>von Nuemann</math> 現在の計算機の原理開発者としても有名)である。\\ |
| - | <math>von Nuemann</math> 現在の計算機の原理開発者としても有名)である。\\ | + | |
鞍点のある問題と異なり,一工夫が必要である。それは,ゲームの利得 | 鞍点のある問題と異なり,一工夫が必要である。それは,ゲームの利得 | ||
| 64 行: | 49 行: | ||
同様に<math>Q</math>が選択する戦略を<math>Q=(q_1,q_2,q_3)</math>で表しておく。\\ | 同様に<math>Q</math>が選択する戦略を<math>Q=(q_1,q_2,q_3)</math>で表しておく。\\ | ||
| - | + | ||
| - | + | <math>P</math>がグーを出し,<math>Q</math>もグーを出す確率は<math>p_1・q_1</math>でこのとき | |
| + | |||
<math>P</math>は損得なし(0円の儲け), | <math>P</math>は損得なし(0円の儲け), | ||
| - | + | ||
| - | + | <math>P</math>がグーを出し,<math>Q</math>がチョキを出す確率は<math>p_1・q_2<math>でこのとき,<math>P</math>は10円の儲け, | |
| - | + | ||
| + | <math>P</math>がグーを出し,<math>Q</math>がパーを出す確率は<math>p_1・q_3<math>でこのとき, | ||
<math>P</math>は10円の損失(-10の儲け), | <math>P</math>は10円の損失(-10の儲け), | ||
| - | |||
という計算を全て行うと | という計算を全て行うと | ||
| 274 行: | 260 行: | ||
最初の<利得表2>を用いれば,<math>E(P^*,Q^*)</math>も求まる。 | 最初の<利得表2>を用いれば,<math>E(P^*,Q^*)</math>も求まる。 | ||
| - | |||
2020年11月24日 (火) 12:17時点における版
\(P,Q\)の2人がじゃんけんをする。\\ 負けたら10円を相手に払い,勝ったら相手から10円貰うというルールで, じゃんけんを繰り返す。\\ 無論,「アイコ」の場合は,支払うお金,貰うお金とも0円である。\\
\(P\)と\(Q\)の出す手によって,貰えるお金,支払うお金がどうなるか, \(P\)の立場で以下のように
「-10」は\(Q\)に10円払う事を表す。\\
\(P\)の立場に立ってみます。先ず,このゲームの利得表には鞍点がない。
双方が選択の余地のない「平衡状態」にする戦略はないわけである。出す手をランダムしてゲームを繰り返す方法以外ない。
このような問題を混合戦略問題といいます。 \\
じゃんけんを繰り返すわけであるが,どのような「戦略」があるか?\\
グーを出し続けとすると,\(Q\)はそれを直ぐ見破って,
パーを出し続けてくるであろう。続ければ続けるほど\(P\)は大損である。\\
同様にパーを出し続けても,チョキを出し続けるのも駄目である。\\
結局,例えば,サイコロを用意して,出た目によって出す手を決めるランダムな手の繰り返す方法であろう。\\
(1か6ならグー,2か5ならパー,3か4ならチョキなど) \\
問題は,どんな割合で(確率で)グー,チョキ,パーを出すべきかである。\\ 相手の\(Q\)は\(P\)の出す手を監視しながら \(P\)と対戦するので,\(P\)が選択したグー,チョキ,パーの確率を直ぐに見破り, それでも,自分にとって有利 な手を選択してくると考えるべきである。\\ \(P\)と\(Q\)の立場を替えても全く同じである。\\
ゲームの理論を創始し,この種の問題に解を与えたのが,ノイマン(\(von Nuemann\) 現在の計算機の原理開発者としても有名)である。\\
鞍点のある問題と異なり,一工夫が必要である。それは,ゲームの利得 \(G(P,Q)\)の替わりに期待値\(E(P,Q)\)を使います。以下、その説明をする。
\(P\)が選択する戦略(グー,チョキ,パーを出す確率)を\(p_1,p_2,p_3\)とし, \(P=(p_1,p_2,p_3)\)で表しておく。\\
このゲームの場合、「戦略」は幾つかある「手」をランダムに選んで繰り返す 確率の組み合わせになるわけである。\\
同様に\(Q\)が選択する戦略を\(Q=(q_1,q_2,q_3)\)で表しておく。\\
\(P\)がグーを出し,\(Q\)もグーを出す確率は\(p_1・q_1\)でこのとき
\(P\)は損得なし(0円の儲け),
\(P\)がグーを出し,\(Q\)がチョキを出す確率は\(p_1・q_2<math>でこのとき,<math>P\)は10円の儲け,
\(P\)がグーを出し,\(Q\)がパーを出す確率は\(p_1・q_3<math>でこのとき, <math>P\)は10円の損失(-10の儲け),
という計算を全て行うと
\(P=(p_1,p_2,p_3),Q=(q_1,q_2,q_3)\) での\(P\)の儲けの期待値\(E(P,Q)\)は \( E(P,Q)=0・p_1・q_1+10・p_1・q_2+(-10)・p_1・q_3\\ +(‐10)・p_2・q_1+0・p_2・q_2+10・p_2・q_3 \\ +10・p_3・q_1+(‐10)・p_3・q_2+0・p_3・q_3 \)
である。 \(P=(p_1,p_2,p_3),Q=(q_1,q_2,q_3)\)は それぞれ,グー,チョキ,パーを出す確率を表しているから, これらについての制約は \( 1 \ge p_1 \ge 0,1 \ge p_2 \ge 0,1 \ge p_3 \ge 0, p_1+p_2+p_3=1\\ 1 \ge q_1 \ge 0,1 \ge q_2 \ge 0,1 \ge q_3 \ge 0, q_1+q_2+q_3=1 \)
である。
簡単のため\(P,Q\)の採り得る集合を \( P_O= \{ (p_1,p_2,p_3)|1 \ge p_1 \ge 0,1 \ge p_2 \ge 0,1 \ge p_3 \ge 0, p_1+p_2+p_3=1\}\\ Q_O= \{ (q_1,q_2,q_3)|1 \ge q_1 \ge 0,1 \ge q_2 \ge 0,1 \ge q_3 \ge 0, q_1+q_2+q_3=1\} \)
で表しておく。前節の\(P_0,Q_0\)と異なり,それぞれ,確率を要素にもつベクトルの 集合になっている。
\(P=(p_1,p_2,p_3)\)が\(P_O\)の中から選択されると\(Q\)はこれに対抗して \(E(P,Q)\)が最小になるように (自分の損失が最小になるように) \(Q=(q_1,q_2,q_3)\)を\(Q_O\)中で選択するはずである。\\ すなわち
\(\min \{ E(P,Q) |Q \in Q_O\}\)
が実現されるとなるような\(Q\)を\(Q_O\)の中で探す。\\ この最小値を \(\min_Q E(P,Q)\) で表しておく。\\ \(P\)はこれを見越して,自分の利益が最大になるようにするため,
\(\max \{ \min_Q E(P,Q) |P \in P_O\}\)
が実現されるとなるような\(P\)を\(P_O\)の中から探すことになる。 この最大値を \(\max_P \min_Q E(P,Q) \) で表しておく。
まっく逆のQの立場からは, \(Q=(q_1,q_2,q_3)\)が\(Q_0\)の中から選択されると\(P\)はこれに対抗して \(E(P,Q)\)が最大になるように \(P=(p_1,p_2,p_3)\)を\(P_0\)中で選択するはずである。\\ すなわち
\(\max \{ E(P,Q) |P \in P_O\}\)
が実現されるとなるような\(P\)を\(P_0\)の中から探す。この最小値を \(\min_P E(P,Q)\) で表しておく。 \(Q\)はこれを見越して,自分の損失を最小にするため,
\(\min \{ \max_P E(P,Q) |Q \in Q_O\}\)
が実現されるとなるような\(Q\)を\(Q_0\)の中で探すことになります。この最大値を \(\min_Q \max_P E(P,Q)\) で表しておく。
以上出てきた,2つの値には一般には
\(\max_P \min_Q E(P,Q) \le \min_Q \max_P E(P,Q)\)
という関係が成り立っている。
ノイマンは上のような問題では,\(P_O,Q_0\)の中に \(P^*=(p_1^*,p_2^*,p_3^*), Q^*=(q_1^*,q_2^*,q_3^*)\) があって \( \max_P \min_Q E(P,Q) = \min_Q \max_P E(P,Q)=E(P^*,Q^*)\\ \max_P E(P,Q^*)=E(P^*,Q^*)= \min_Q E(P^*,Q) \)
となることを証明した。\\
この\(P^*<math>と<math>Q^*<math>を具体的求めることにする。\\ 問題を解きやすくするため,最初に出てきた<利得表> (損失と利益の表)の要素に全て10を加えて おく。\\ <利得表2>\\ \begin{tabular}{|c|c|c|c|} \hline &<math>Gu<math>&<math>Choki<math>&<math>Pa<math>\\ \hline <math>Gu<math>&10&0&20 \\ \hline <math>Choki<math>&20&10&0\\ \hline <math>Pa<math>&0&20&10 \\ \hline \end{tabular} <math> Gu:グー\\ Choki:チョキ\\ Pa:パー \)
これでは,一方的な\(P\)のゲームになるかもしれないが,\\ \(P^*=(p_1^*,p_2^*,p_3^*),Q^*=(q_1^*,q_2^*,q_3^*)\) を計算するためだけであり,このような,利得表の平行移動やっても解は同じである。\\
\(P^*<math>も,<math>Q^*<math>も,<math>E(P^*,Q^*)\)も未知な量であるが
\(E(P^*,Q^*)\)は判っているもの
として
\(\max_P E(P,Q^*)=E(P^*,Q^*)=\min_Q E(P^*,Q)\)
に注目する。 \( E(P,Q)=q_1 \{ 10p_1+0p_2+20p_3\} \\ +q_2 \{ 20p_1+10p_2+0p_3\} +q_3 \{ 0p_1+20p_2+10p_3\} \)
で, \(1 \ge q_1 \ge 0,1 \ge q_2 \ge 0,1 \ge q_3 \ge 0, q_1+q_2+q_3=1<math> ですので <math> E(P^*,Q^*) \le 10p_1+0p_2+20p_3~ (1)\\ E(P^*,Q^*) \le 20p_1+10p_2+0p_3~ (2)\\ E(P^*,Q^*) \le 0p_1+20p_2+10p_3~ (3) \)
という条件を満たせば,任意の\(Q \in Q_0\)について
\(E(P^*,Q^*) \le E(P,Q)\)
が成り立つ。従って
\(E(P^*,Q^*) \le \min_Q E(P,Q)\)
が成り立つ。\\ \((1)\)~\((3)\)と\(P \in P_0\)即ち \\ \(1 \ge p_1,p_2,p_3 \ge 0, p_1+p_2+p_3=1<math> の制約条件下で <math>E(P,Q^*)=\max_P E(P,Q^*)\)となる\(P\) を求めれば, \(E(P,Q^*)=E(P^*,Q^*)\) となるわけである。 しかし,これではまだ\(E(P^*,Q^*)\)が未知量であるので,
\((1)\)~\((3)\)の両辺を\(E(P,Q^*)\)で割り, \( r_1=p_1/E(P,Q^*)\\ r_2=p_2/E(P,Q^*)\\ r_3=p_3/E(P,Q^*) \)
として, \(E(P^*,Q^*)/E(P,Q^*) \ge 1<math> に注意すると <math> 1 \le 10r_1+0r_2+20r_3~(1') \\ 1 \le 20r_1+10r_2+0r_3~(2') \\ 1 \le 0r_1+20r_2+10r_3~(3') \) \( r_1+r_2+r_3 \\ =(p_1+p_2+p_3)/E(P,Q^*)\\ =1/E(P,Q^*) \)
から
\(E(P,Q^*)のPについての最大化 \Leftrightarrow 「r_1+r_2+r_3の最小化」<math> 結局,線形計画法の問題 <math> 1 \le 10r_1+0r_2+20r_3(1') \\ 1 \le 20r_1+10r_2+0r_3(2') \\ 1 \le 0r_1+20r_2+10r_3(3') \)
かつ
\(r_1,r_2,r_3 \ge 0\) の制約条件で
\(r_1+r_2+r_3<math> を最小化する\\ という問題が出てくる。 Microsoft Excel のsolver などツールが利用できる。 その解から <math> p_1^*=r_1/(r_1+r_2+r_3) \\ p_2^*=r_2/(r_1+r_2+r_3) \\ p_3^*=r_3/(r_1+r_2+r_3) \)
とすれば,\(P^*<math>の最適戦略が求まる。\\ <math>P\)と\(Q\)の役目を交換しても全く同じなので,\(P^*=Q^*<math>である。 最初の<利得表2>を用いれば,<math>E(P^*,Q^*)\)も求まる。