線形計画法(生産計画)
提供: Internet Web School
| 38 行: | 38 行: | ||
<math> | <math> | ||
| - | 2x+y \qquad (6) | + | f(x,y)=2x+y \qquad (6) |
</math> | </math> | ||
| 44 行: | 44 行: | ||
| - | 下の図は関数<math> | + | 下の図は関数<math>f(x,y)=2x+y</math>の図である。 |
| 73 行: | 73 行: | ||
<math> | <math> | ||
| - | f(x,y)=2x+y \qquad ( | + | f(x,y)=2x+y \qquad (6) |
</math> | </math> | ||
には「線形性」が成り立っている. | には「線形性」が成り立っている. | ||
| 88 行: | 88 行: | ||
=\alpha f(x,y)+\beta f(x',y')=\alpha f(P)+\beta f(Q) | =\alpha f(x,y)+\beta f(x',y')=\alpha f(P)+\beta f(Q) | ||
</math> | </math> | ||
| + | |||
という性質である。この線形性を使うと,以下の議論ができる。 | という性質である。この線形性を使うと,以下の議論ができる。 | ||
まず各頂点での関数<math>f</math> | まず各頂点での関数<math>f</math> | ||
| + | |||
<math> | <math> | ||
f(P_i)=f(x_i,y_i),i=0,1,2,3,4 | f(P_i)=f(x_i,y_i),i=0,1,2,3,4 | ||
</math> | </math> | ||
| - | |||
| - | + | のうち最大値を<math>f(P_*)=f(x_*,y_*)</math>とする. | |
| + | |||
| + | 凸多角形の内の任意の点<math>P=(x,y)</math>に対する<math>f(P)=f(x,y)</math>は | ||
| - | <math>P</math>が<math>P_i=(x_i,y_i),i=0,1,2,3,4</math>の凸結合で表されることから | + | <math>P</math>が<math>P_i=(x_i,y_i),i=0,1,2,3,4</math> |
| + | の凸結合で表されることから | ||
<math> f(P)=f(\lambda_0 P_0 + \lambda_1 P_1+\lambda_2 P_2+\lambda_3 P_3+\lambda_4 P_4)</math> | <math> f(P)=f(\lambda_0 P_0 + \lambda_1 P_1+\lambda_2 P_2+\lambda_3 P_3+\lambda_4 P_4)</math> | ||
2020年11月25日 (水) 15:51時点における版
生産計画
ある製造会社があって, \(x\)と\(y\)という2種類の製品の製造販売をしている. これらを製造するには, 原材料\(A\),\(B\),\(C\)が必要で, \(x\), \(y\)をそれぞれ1単位当 たり造るのに必要な量と, 使用できる在庫量が下の表のように決まっている. \( \begin{center} \begin{tabular}{cccc} & x & y & (在庫量) \\ A & 10 & 20 & 400 \\ B & 20 & 10 & 600 \\ C & 15 & 40 & 1300 \end{tabular} \end{center} \) \(x\), \(y\)を販売するとそれぞれ1単位当たり2万円, 1万円の利益が得られる. 問題は, 表の在庫量の範囲で, \(x\)と\(y\)をそれぞれ何単位ずつ造れば利益が最大に なるかである。
これを数式化すると, \(x\), \(y\)の製造量を\(x\), \(y\)で表すとして:
原材料\(A\), \(B\), \(C\)についての制約から
\( 10x+10y\leq 400 \qquad (1) \\ 20x+10y\leq 600 \qquad (2) \\ 15x+40y\leq 1300 \qquad (3) \)
負の生産量はないのであるから
\( 0\leq x \qquad (4) \\ 0\leq y \qquad (5) \\ \)
利益は
\( f(x,y)=2x+y \qquad (6) \)
で結局, (6)を\((1)\sim (5)\)の条件のもとで最大にすることになる。
下の図は関数\(f(x,y)=2x+y\)の図である。
\vspace{5cm}
\par
(図1.0)\\
条件\((1)\sim (5)\)を充たす点\(P=(x,y)\)は 下のような,凸多角形の境界線も含めた内部にある。
(図1.1)\\
この凸多角形の頂点を \( P_0=(x_0,y_0),P_1=(x_1,y_1),P_2=(x_2,y_2),P_3=(x_3,y_3),P_4=(x_4,y_4) \) とすると, 内部の点\(P=(x,y)\)はこれらの頂点\(P_i=(x_i,y_i),i=0,1,2,3,4\)によって
\( (1) \qquad P=\lambda_0 P_0 + \lambda_1 P_1+\lambda_2 P_2+\lambda_3 P_3+\lambda_4 P_4 \\ (2) \qquad \lambda_0 + \lambda_1 +\lambda_2 +\lambda_3 +\lambda_4 =1 \\ (3) \qquad 0 \le \lambda_0 \le 1,~~0 \le \lambda_1 \le 1,~~2 \le \lambda_2 \le 1, 0 \le \lambda_3 \le 1,~~0 \le \lambda_4 \le 1 \)
で表される。これを\(P_i=(x_i,y_i),i=0,1,2,3,4\)の凸結合という.
\( f(x,y)=2x+y \qquad (6) \) には「線形性」が成り立っている.
これは \( P=(x,y),Q=(x',y') \)
と\(\alpha,\beta\)について,
\( f(\alpha P+ \beta Q)=f(\alpha (x,y)+\beta (x',y') =\alpha f(x,y)+\beta f(x',y')=\alpha f(P)+\beta f(Q) \)
という性質である。この線形性を使うと,以下の議論ができる。
まず各頂点での関数\(f\)
\( f(P_i)=f(x_i,y_i),i=0,1,2,3,4 \)
のうち最大値を\(f(P_*)=f(x_*,y_*)\)とする.
凸多角形の内の任意の点\(P=(x,y)\)に対する\(f(P)=f(x,y)\)は
\(P\)が\(P_i=(x_i,y_i),i=0,1,2,3,4\) の凸結合で表されることから
\( f(P)=f(\lambda_0 P_0 + \lambda_1 P_1+\lambda_2 P_2+\lambda_3 P_3+\lambda_4 P_4)\)
さらに\(f\)の線形性から
\( 右辺=\lambda_0 f(x_0,y_0) + \lambda_1 f(x_1,y_1) +\lambda_2 f(x_2,y_2)+\lambda_3 f(x_3,y_3)+\lambda_4f(x_4,y_4) (fの線形性) \)
\(f(P_*)=f(x_*,y_*)\)が最大で,(3)のように各\(\lambda_i\)は正の数(\(1 \ge \lambda_i \ge 0\))であるから,
\( 右辺\le (\lambda_0 + \lambda_1 +\lambda_2 +\lambda_3 +\lambda_4)f(x_*,y_*)\\ \)
さらに,(2)から
\( \lambda_0 + \lambda_1 +\lambda_2 +\lambda_3 +\lambda_4= 1 \)
で
\( f(P)=f(x,y) \le f(x_*,y_*)=f(P_*) \) となる。結局,関数\(f\)の制約条件を表す凸多角形の内部(境界を含む)の点全てを調べる必要がなく、
頂点での関数\(f\)の値を調べれば良いことが判る.
(図1.2)
線形化計画法の代表的な解法であるシンプレクス法は,制約条件を表す凸多角形の頂点での 関数\(f\)の値を効率的に調べる方法である。 適当な,頂点から始め,関数\(f\)の値が増大する頂点へ次々移動して,最大解を探す.
この他に,凸多角形の内部の点から,最大解を与える頂点を探索する内点法もある。
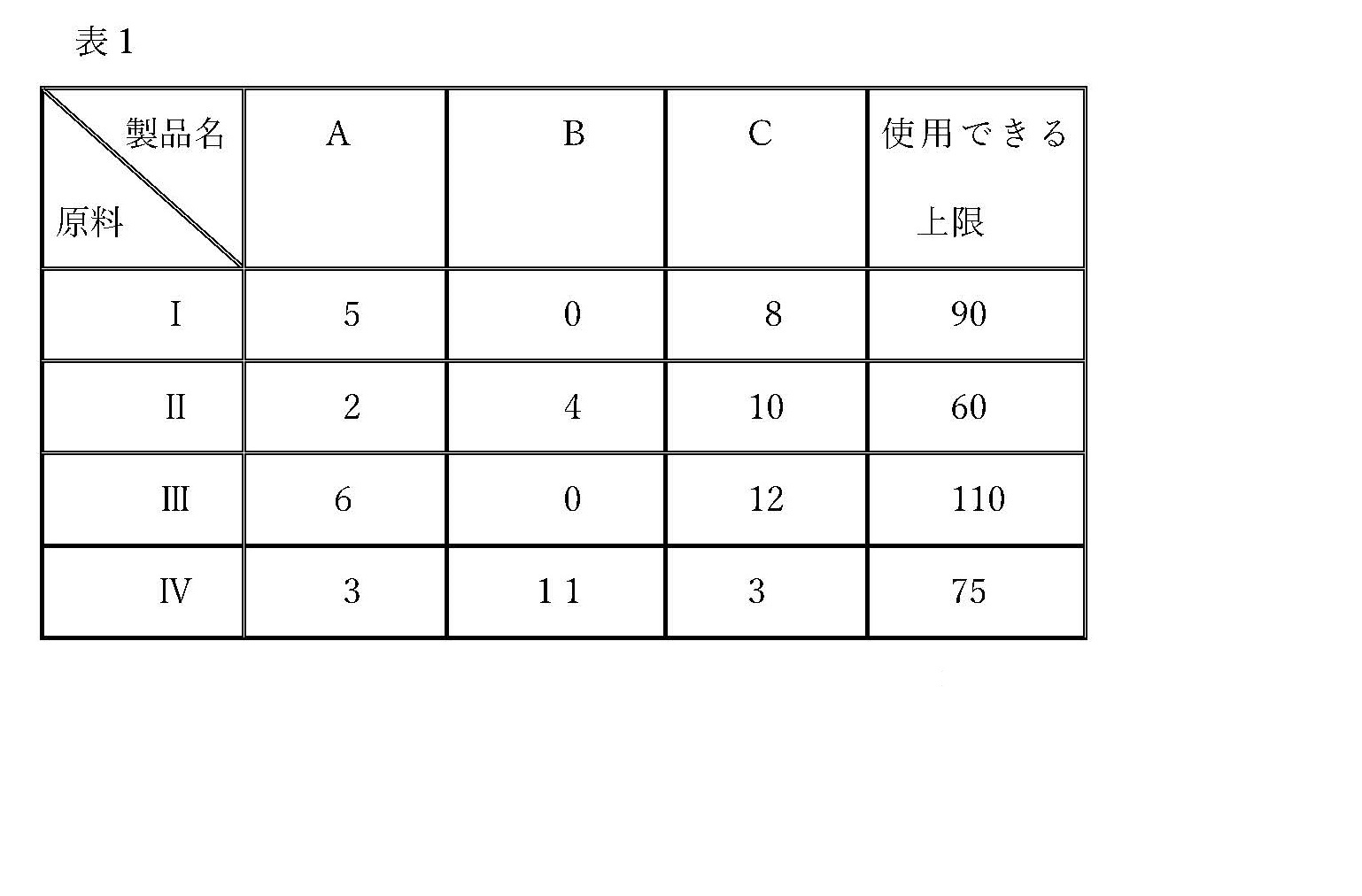
ある企業では製品A,B,Cを原料Ⅰ,Ⅱ,Ⅲ,Ⅳ用いて生産している. 製品A,B,C の1単位当たり利益をそれぞれ80,110,95とする. また, 製品A,B,Cを1単位生産するのに必要な原料Ⅰ,Ⅱ,Ⅲ,Ⅳのそれぞれ量と使用可能な上限が次の表で与えられる. これらの条件のもとに,利益を最大にするには製品A,B,Cをそれぞれ,どれだけ生産すれば良いか?.
この問題は以下のように数学的に定式化される.
線形計画法
製品A,B,Cをそれぞれ\(x_1,x_2,x_3\) 単位生産するとき\(x_1,x_2,x_3\)は以下の不等式を満たす.
\( 4x_1+0x_2+7x_3 \leq 90 \\ 1x_1+3x_2+9x_3 \leq 60 \\ 6x_1+0x_2+14x_3 \leq 110 \\ 4x_1+10x_2+1x_3 \leq 75 \qquad (1) \)
さらに各製品生産量は負ではないから
\( 0 \leq x_1,0 \leq x_2,0 \leq x_3 \qquad (2) \)
この制約条件のもとに
\( L\left(x_1,x_2, x_3 \right)=80x_1+110x_2+95x_3 \qquad (3) \)
を最大にする\(x_1,x_2, x_3\)を求めよ.
\((1)\)式のように変数に関する制約条件式が1次式で与えられ,
\((3)\)式のように評価関数も1次式で与えられる問題は線形計画法と呼ばれる.
この問題の解法にはシンプレックス法や内点法がある.
シンプレクス法は[菅沼]の解説が判りやすい.
この問題を解くのにはMicrosoft Excelのソルバーや
フリーソフトのOpen Office で提供されるソルバーと同等の機能をもつソフトを用いることができる.
この問題のMicrosoft Excelのソルバーによる解法例を示す。 ファイル:生産計画.pdf