数学・解析/積分
提供: Internet Web School
(版間での差分)
(→区分求積法) |
|||
| 1 行: | 1 行: | ||
[[数学・解析]] | [[数学・解析]] | ||
> [[数学・解析/積分|積分]] | > [[数学・解析/積分|積分]] | ||
| - | |||
| - | |||
* [[wikipedia_ja:Portal:数学|Wikiポータル 数学]] | * [[wikipedia_ja:Portal:数学|Wikiポータル 数学]] | ||
| + | |||
| + | == 目次 == | ||
* [[wikipedia_ja:不定積分|不定積分]] | * [[wikipedia_ja:不定積分|不定積分]] | ||
2011年8月26日 (金) 08:42時点における版
数学・解析 > 積分
目次 |
目次
解説
不定積分
関数 を微分した関数(導関数)が
のとき、
を
の不定積分または原始関数といい、
と表します。 が x の連続関数ならその不定積分は必ず存在し、加える定数だけを除いて一意的に決まります。
のとき、
となります。C は定数で、積分定数といいます。
積分(定積分)
の不定積分を
で表すとき、
となり、これを与えられた区間 の上での積分と言います。
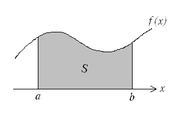
区分求積法
の区間
の上での積分
は、右図の面積 S を表します。