物理/波の性質
提供: Internet Web School
(→波の伝搬速度 ) |
(→単振動と正弦波 ) |
||
| 308 行: | 308 行: | ||
$y=h(t)=A\sin ((kt+\phi) $<br/> | $y=h(t)=A\sin ((kt+\phi) $<br/> | ||
であり、単振動であることが分かる。証明終わり。<br/> | であり、単振動であることが分かる。証明終わり。<br/> | ||
| + | ===波の伝搬速度 === | ||
| + | 気体や水や固体を媒質を小さな部分に分割して,それら分割部分の<br/> | ||
| + | 平衡状態からの変位と隣接する分割部分から受ける力の関係を求め、<br/> | ||
| + | ニュートンの運動法則を適用することで,波動方程式と呼ばれる | ||
| + | 波の運動方程式が導出できる。<br/> | ||
| + | 電磁波の運動方程式は、電磁気学の法則(マクスウェル方程式)を用いて得られる。<br/> | ||
| + | 波動方程式から波の伝搬速度が得られる。<br/> | ||
| + | 波の伝搬速度は、<br/> | ||
| + | 媒質(平衡点からの変位と復元力の関係)と縦波か横波かで決まり、<br/> | ||
| + | 振幅や振動数には無関係である。<br/> | ||
| + | これらについては、「4.4 弾性波の力学的考察」で簡単に紹介する。<br/> | ||
| + | 興味のある方は、インターネットで、「波動方程式」を検索して、分かりやすい記事を探して読んでください。 | ||
| + | |||
===波の重ね合わせの原理=== | ===波の重ね合わせの原理=== | ||
後述(4.5)するように、波の運動方程式である、波動方程式は[[wikipedia_ja:線形性|線形性]] をもつので、<br/> | 後述(4.5)するように、波の運動方程式である、波動方程式は[[wikipedia_ja:線形性|線形性]] をもつので、<br/> | ||
2016年4月27日 (水) 18:33時点における版
目次 |
波の性質
波には色々あるが、この節では波に共通する性質を学ぶ。
波の次元
張った弦の振動のように、一次元空間を伝わる波を一次元の波、
水面のような2次元の空間を伝わる波を2次元の波、
空中や水中を伝わる音のように、3次元空間を伝わる波を3次元の波という。
==波面と波面の形 ==$W(t)$
波線・波面; 波の山をつないだ図形や波の谷をつないだ図形のこと。
2次元の波では曲線になり波線という。
3次元の波では曲面になり波面という。
波面が平面になる3次元の波を平面波という。
また波面が球面になる3次元の波を球面波という。
一様で、方向性のない3次元の媒体中の一点に変位を与え波を発生させると、
この点波源から全く同じ性質の波が、あらゆる方向に伝わっていくので、
波面は球面になる。
この球面波を波源から十分離れた場所で観測すると、
観測点の近くの限定された空間内では、平面波とみなせる。
波の進行方向 と速度
ある時刻tにおける波面$W(t)$を、その微小時間 $\delta t(>0)$後に観測すると、
その位置を少し変えている。その波面を$W(t+\delta t)$ とかく。
時刻 t の波面の一点 P から、
この波面に直行する直線をひき、波面$W(t+\delta t)$ との交点を P' とすると、P' は波面$W(t)$上の一点Pが進行した場所と考えられる。
波の PP'間における平均速度は、 $\frac{PP'}{\delta t}$ である。
$\lim_{\delta t \to 0}$ をとると、波面の一点Pにおける、時刻tの瞬時速度が得られる。
波の発生の仕組みと連続波とパルス波、縦と横波
変位に対して、もとに戻ろうとする力が生じる物質(注)では、
ある場所にわずかな、変位が与えられると
元の位置に戻ろうとして振動を生じ(波源)
これが隣接する媒質に力を与えて隣接部に振動をおこし、
物質(媒質)全体に振動が伝わっていく。
これが波である。
(注)変位に対して復元力の働く性質のことを弾性といい、
弾性が原因でおこる波を弾性波という。
連続波とパルス波
波源の振動の持続回数により、2種類の波がおこる。
波源が連続的に振動し続ける場合には、
波源から連続的に波が生み出され、媒質全体に伝わって行くので、
連続する波がが生じる。連続波という。
また波源が一回の振動で変位がなくなる場合には、
一つの山(ないし谷)の波が波源から放出され、媒質の中を伝わっていく。
パルス波という。
縦波と横波
媒質がどのような変形に対して復元力を持つかに応じて、異なった形の波動が生じる。
縦波
圧縮・膨張に対する復元力を持つ媒質では、波源が急激に変位すると、
その変位方向の2つの隣接部分の一方は、圧縮され密になり、他方は膨張し租になる。
すると圧縮側の圧力がその隣接部分の圧力より高くなり、その部分を圧縮する。
こうして圧力の高い部分が媒質の振動方向の片側を伝わっていく。
他方、媒質の変位により、膨張した側では、圧力がその隣接部分より小さくなり、
隣接部分からおされて圧縮され圧力を回復していくが、隣接部分は圧力を下げる。
こうして、圧力の低い部分が、媒質の振動方向の逆側を伝わっていく。
この波は、媒質の振動が波の進行方向と平行なので、
縦波(longitudinal waves)という。
横波
媒質が横ずれに対して復元力を持つ場合では、別のタイプの波が生じる。
この場合、波源が変位したとき、
波源は、変位方向と直角(上下と表現する)の隣接部分と引き合って、引きずる。
このため、波源の左右への振動により、
上下にある隣接部分もやや遅れて引きずられて
左右に振動しこれが媒質全体に伝わっていく。
この波の進行方向(上下)と、媒質の振動方向(左右)は直交するので、
横波(transverse waves)という。
気体や流体は、横ずれに対して復元力を持たないため、横波は発生しない。
横波でも縦波でもない波
横波でも縦波でもない波もある。後述する水面の波が、その例である。
弾性波
弾性波
媒質の変位により生じる波を弾性波と呼ぶ。 縦波、横波は弾性波である。
弾性波を生じない物質
2章で述べたように、かたい固体を理想化して、全く変形しない固体を考えて、剛体と名付けた。
剛体では、圧縮、変形が起こらないので、剛体の中には波は発生しない。
現実の物質は弾性波を生じる
現実の物質は圧力をかければ、程度の差はあるが、圧縮し、元のもどろうとする力が発生するので、縦波はおこる。
弾性波でない波
光や電波は電磁波という波の一種だが、媒質はない。
真空中でもこの波は発生する。
あえて言えば、電磁波では、真空という空間が媒質で、
電気的な空間のゆがみ(電場、磁場)の振動が伝搬して起こる
横波と考えられる(電磁波については10章で学ぶ)。
次の記事も参考に。
波の例
身の回りには色々な波が良く見られる。
媒質が空気である波は音(あるいは音波)であり、縦波である。
媒質が水の場合は水面波や水中の音波となる。
水面のさざ波や小さな波(水面波)は、
水の表面張力や重力が、ずれに対する復元力になるので,横波の成分をもつ。
ところが、ある場所の水面が上下振動しても、
その鉛直下方にある水は殆ど膨張・圧縮されないので、
水面上昇時には隣接する水面下の水が流れ込み、下降時には、鉛直下方の水が隣接する水面の下方に押し出され、
波の進行方向する方向と平行の振動が起こる(注)。
こうして水の表面の水粒子は波が通過するとき、上下の振動に、
波の進行方向と平行な振動を合成した、円形(あるいは楕円形)の振動をする。
従って、縦波でも横波でもない。
音叉は媒質が金属で、其の一か所に打撃を与えて変位を起こすと、
ずれや曲げに対する復元力から振動が起き、それが音叉全体に伝わる。
これは縦波である。
この音叉の振動で周囲の空気が圧縮・膨張の振動を発生し、これが縦波となって、音波を生じさせる。
バイオリンは、弓で弦をひいて、弦の振動を引き起こし、この振動が横波となり弦全体や胴に伝達し、楽器全体を振動させる。
これが周りの空気の振動を引き起こし、音波として伝搬する。
固体は曲げやずれに対する復元力を持つので横波を起こすが、
わずかとはいえ、圧縮・膨張して、強い復元力を生じるため、縦波も起こす。
地震波は地殻の波だが
最初に到達するP波は縦波で、
遅れて到達するS波は横波である。
地表へは、地震波は下方から到達するので、縦波のP波は上下動、横波のS波は横揺れになる。
例のまとめ;
縦波の例;音波、地震のP波(第一波)。媒質はそれぞれ空気と地殻。
$\qquad$媒質の圧縮と膨張により波が起き、伝達する。
横波の例;金属の振動、張った糸や弦の振動、地震のS波。媒質はそれぞれ、金属、糸、弦、地殻である。
$\qquad$媒質の横ずれに対する復元力から波が生じ、伝達する。
縦波でも横波でもない波の例;水面波
波形の数式による表示
波は、任意の位置 $\vec x$ と任意の時刻 $t$ における,
媒質の平衡状態(波がない静止状態)からの変位量であらわせる。
変位量について
波は、媒質を連続体としてみれば、
媒質の一部の振動が、隣接する媒質の振動を引き起こし、
次々と媒質の振動が伝搬していく現象である。
これを微視的にみれば、
媒質を構成する分子の運動(注1)が次々と隣接する分子の運動を引き起こし、
運動が伝搬する現象である。
しかし膨大な数(注2参照)の個々の分子の、
運動を時間的に追うことは不可能であろう。
また我々が知りたいのは、
媒質の個々の分子の運動の平均的な結果として生じる、
波の圧力や密度、
あるいは媒質の微小部分(巨視的には面積を無視できるが、膨大な数の分子で構成される)の位置の巨視的な変化量
なので、個々の分子の軌道を求める必要もない。
そこで、波の研究では、
媒質の圧力や密度、巨視的な位置変化量などを変位量とし、
これらの変化の法則を見出して、
場所と時間の関数として表わし、
その数式から波の諸性質を求める。
(注1)ある位置を中心にした振動であることが多いが、
波の表面波のように、円運動に近い動きの場合もある。
しかもこれらの運動に熱運動が加わっているため、分子の運動は複雑である。
いづれにしても、媒質自体(それを構成している分子たち)は、波と一緒に動くのではない。
(注2)気体でも標準状態(一気圧、0℃)では1$cm^3$ の中に、
約 $10^{19}$ 個の分子がある。
一辺が$\frac{1}{100}$mmの微小な立方体(正6面体)中にさえ、 $10^{10}$ 個の分子がある。
☆☆ある点での圧力、密度の意味
ある点pでの圧力とか密度というのは、本来は粒子(原子・分子)からなる物質を
連続体とみなして定義した概念で、現実の理想化である。
物質を連続体とみなせば、
ある点pの圧力 $P(p)$ とは、
p点を含む微小平面 $H(p)$ での圧力を $P_{H(p)}$ ,面積を $|S_{H(p)}|$ と書くとき、
$P(p):=\lim_{|S_{H(p)}|\to 0}P_{H(p)}$
である。
しかし、現実には、あらゆる物質は原子・分子から構成されている粒子系であり、連続体ではない。
圧力は3章4節の気体の分子運動論で説明したように、
膨大な個数の気体分子が、熱運動で壁にぶつかり反射するときの、
単位時間、単位面積当たり力積の和できまる(注1参照)。
乱雑・無規則な衝突の壁にあたえる力は、
少数の気体分子の場合には、時間的変動が大きく、
その平均値である圧力は意味を持たない。
しかし、膨大な個数の分子の壁への衝突では、
時間的な変動が打ち消され、殆ど一様な力となるため平均値は意味を持ち、
巨視的な測定もできる。
そのため、$|S_{H(p)}|$を零に近づけていくと、あるところから$P_{H(p)}$
存在しなくなり
$\lim_{|S_{H(p)}|\to 0}P_{H(p)}$
は、不可能である。
現実には、圧力が意味を持つ最小の面積(注2参照)での圧力で近似値を定める。
また、ある点pの時刻tでの密度とは、
時刻tのおけるp点の周りの単位体積当たりの質量のことである。
場所によって密度に粗密があるときは、
時刻tで、p点に非常に近い微小体積 $V(p)$ の媒質の質量
$m_{V(p)}(t)$ を,その体積で割ったもの $\frac{m_{V(p)}(t)}{|V(p)|}$ として定義する。
ここで、 $|V(p)|$ は $V(p)$ の体積である。
物質を連続体と考えるので、体積を零にしていくときの極限
$\lim_{|V(p)|\to 0}\frac{m_{V(p)}(t)}{|V(p)|}$
が、その点における媒質の密度である。
しかし、実際の媒質は、微視的に見れば、
連続体ではなく膨大な数の分子からなる系なので、
分子の大きさのレベルの体積を考えると、その中に分子がいることは殆どなく、
密度は殆ど至る所で零になる。
また分子のいる場所では密度が非常に大きくなる。
また、時刻がわずかに変わるだけでも、分子の運動のためこの場所が乱雑に変動する。
したがって、密度という概念が意味を持つには、ある程度以上の体積の媒質を必要とする。
(注1)気体の圧力Pは、単位時間、単位面積当たりの力積の和である。
厳密には、点pの時刻tでの圧力 $P(p,t)$ とは、
時刻tから $t+\delta t$ の間に、
pを含むある平面のpを含む面素 $H(p)$ へ分子が与える力積の合計値を
$I(H(p),\delta t)$ とかくと、
$P(p,t):=\lim_{\delta t\to 0}\lim_{|H(p)|\to 0}\frac{I(H(p),\delta t)}{|\delta t||H(p)|}$
ここで、 $|H(p)|$ は面積を表す。
(注2)圧力や密度が意味を持つ面や体積の目安は、
分子が互いに衝突するまでに運動する距離(平均自由行程)lを一辺とする
正方形と立方体で与えられる。
標準状態(一気圧、0℃)の気体では、 $l\approx 10^{-6}cm$ である。
また、圧力が意味をもつ時間の目安は、
分子が互いに衝突までの平均時間で与えられ、
標準状態の気体で $10^{-10}s$ 程度である。
これよりはるかに長い時間を周期とし、
lよりはるかに大きい波長をもつ波を扱う場合には、
圧力や密度は、各瞬間に、各点で定義できると考えてよい。
一次元波動の波形の数式表示
3次元の波では、
その波形は、独立変数が4つ(3次元空間の場所と時間)で、数式の扱いは難しくなり、
図示は不可能である。
一次元の波では、その波形の数式表示は簡潔である。
しかし、その応用範囲は広い。
たとえば、
張った弦や糸の振動などは一次元の横波である。
また、3次元空間の平面波も進行方向をx軸にえらべば、
この軸の上を伝わる一次元波動とみなせる。
同様に球面波は、波源からあらゆる方向に
速度も振動の仕方も全く同じ一次元波が放射されるので、
ひとつの一次元波を解析すればよい。
初期時刻の波形の表示
時刻の原点(初期時刻)を考察しやすいように選ぶ。
波の進行方向をx軸の正方向にとる。
波の変位量(縦波では媒質の圧力、横波では、媒質の巨視的な位置の変化量)をy軸にとる。
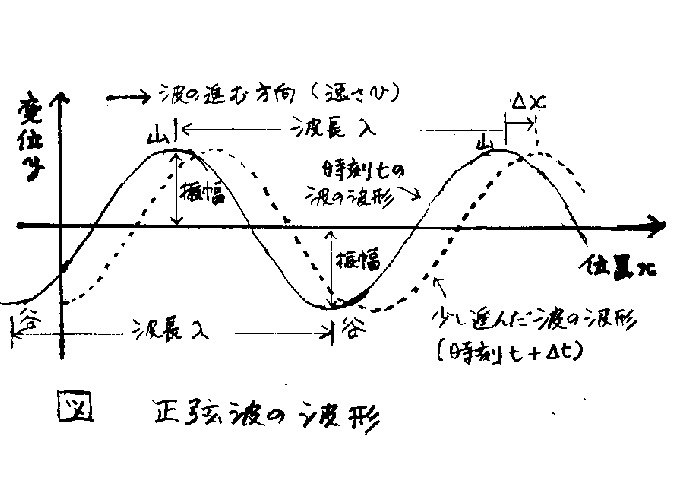
一例とした、後述する正弦波の波形を図示する。
実線は時刻tでの波形、
点線は、その微小時間後の時刻$t+\Delta t$の波形である。
波は、x軸の正方向に進行している。
一般の波の初期時刻における波形が
$y=f(x)\qquad \qquad (1)$
と数式表示されるとする。
波がx軸正方向に速度 $v$ で進行しているとき(注参照)、
時刻tの波形はどのように表示されるだろうか。
(注)vが負の時は、x軸の負の方向に進む。
時刻tの波形の表示
式(1)で与えられる波がx軸の正方向に速度 $v$ で進行しているとき(注参照)、
任意の時刻tの波形はどのように表示されるだろうか。
命題 4.1
時刻0の波形を、
$y=f(x)\qquad \qquad (2)$
とする。
この波が、x軸の正方向に速度 $v$ で進行するとき、
その波は、
$y=f(x-vt)$
で表せる。
証明;
任意の時刻tの波形を $y=g(x,t)$ とかく。
この波形は、式(2)の波形をx軸の正方向に $vt$ 平行移動したものであるから、
式(2)の波形のxでの変位量$f(x)$は、
時刻tの波形では、 $x+vt$ の位置になっている。
数式で書くと
$f(x)=g(x+vt,t)$
$x$ に $x-vt$ を代入すると
$y=g(x,t)=f(x-vt)\qquad \qquad (3)$
これが、速度vでx軸の正方向に進む1次元の波の一般形である。
(注)vが負の時は、x軸の負の方向に進む。
単振動と正弦波
媒質の振動のうちもっとも基本的なものは、
正弦関数にしたがって振動する単振動である。
yを変位として数式で書くと
$y=A\sin(kt+\theta)$
代表例は、ばねにつながれたおもりの運動である。
ばねは、おもりの変位をなくそうと、変位量に比例した力を作用させる。(フックの法則)
この結果、おもりは単振動を行う。
- ウィキペディア(自由振動) の 1 単振動 参照。
単振動の振動数、周期と角振動数(角速度)
正弦波
波形が正弦関数であらわせる波を正弦波という。
振幅がAで、初期位相 $\theta$ の正弦波の初期時刻の波形は,一般に
$y=f(x)=A\sin (kx+\theta)$
と書ける。
この波が速度vで進むとき、その波は、命題4.1により
$y=f(x-vt)=A\sin \left(k(x-vt)+\theta\right)\qquad \qquad (5)$
命題4.2
1次元の正弦波の波形は、
振幅をA、波長を$\lambda$, 速度をv とし、
初期時刻の位相を $\theta$ すると、
$y=A\sin(\frac{2\pi}{\lambda}(x-vt)+\theta) \qquad \qquad (4)$
で表せる。
(証明)
式(5)より、
$y=f(x-vt)=A\sin \left(k(x-vt)+\theta\right)$
正弦波の波長が $\lambda$ なので、
$\lambda$ごとに同じ波形があらわれなければならない。
そのためには
$k\lambda =2\pi $
でなければならない。
これより、 $k=\frac{2\pi}{\lambda}$ が得られる。
周期的な波の波長、振動数、周期、速度の関係
命題4.3
正弦波に代表される周期的な波(注)の
波長を$\lambda$、振動数を$f$、周期を$T$ 速度の大きさを$v$とする。
これらには次の関係がある。
(1) $T=\frac{1}{f},\quad f=\frac{1}{T}$
(2) $v=\lambda \qquad f=\frac{\lambda }{T}$
(注)一定の間隔(周期)ごとに同じ波形を繰り返す波のこと。
命題4.4
任意の場所xで、正弦波を観測すると、
単振動を行う。
証明;
命題4から、正弦波は
$y=A\sin \left(\frac{2\pi}{\lambda}(x-vt)+\theta\right) $
で表される。
この式で、xを固定し、tの関数 $h(t)$ としてみると
$y=h(t)=A\sin \left(-v\frac{2\pi}{\lambda}t+(\frac{2\pi}{\lambda}x+\theta)\right) $
この式で、$-v\frac{2\pi}{\lambda}$ を $k$で、
$\frac{2\pi}{\lambda}x+\theta$ を $\phi$ で表すと、
$y=h(t)=A\sin ((kt+\phi) $
であり、単振動であることが分かる。証明終わり。
波の伝搬速度
気体や水や固体を媒質を小さな部分に分割して,それら分割部分の
平衡状態からの変位と隣接する分割部分から受ける力の関係を求め、
ニュートンの運動法則を適用することで,波動方程式と呼ばれる
波の運動方程式が導出できる。
電磁波の運動方程式は、電磁気学の法則(マクスウェル方程式)を用いて得られる。
波動方程式から波の伝搬速度が得られる。
波の伝搬速度は、
媒質(平衡点からの変位と復元力の関係)と縦波か横波かで決まり、
振幅や振動数には無関係である。
これらについては、「4.4 弾性波の力学的考察」で簡単に紹介する。
興味のある方は、インターネットで、「波動方程式」を検索して、分かりやすい記事を探して読んでください。
波の重ね合わせの原理
後述(4.5)するように、波の運動方程式である、波動方程式は線形性 をもつので、
波は重ね合わせが出来る。
一つの波が来たときの媒質の変位$ y_1$ と他の波が来たときの媒質の変位を$ y_2$ とすると、
この2つの波が同時に来た時の媒質の変位は$ y=y_1+y_2$となる。これを波の重ね合わせの原理という。
重ね合わせて出来る波を合成波という。
この原理は以下のように、多くの現象の分析・解析に応用できる。
複雑な形の波
一般の複雑な形の波は、
周期や振幅の異なるいくつかの正弦波を重ね合わせたものと考えることができる。
これについては大学の専門課程で学ぶ(フーリエ解析と呼ばれる)。
定常波と進行波
定常波(ていじょうは、standing waveまたはstationary wave)とは、
波長・周期(振動数または周波数)・振幅・速さ(速度の絶対値)が同じで
進行方向が互いに逆向きの2つの波が重なり合うことによってできる、
波形が進行せずその場に止まって振動しているようにみえる波動のことである。
定在波(ていざいは)ともいう。(下記のウィキペディアの記事の冒頭より)。
命題 4.5
波長$\lambda$,振幅A、速さ(速度の絶対値)vが同じで
進行方向が互いに逆向きの2つの波が重なり合うと、
波形が進行せずその場に止まって振動しているようにみえる波動となる。
証明;
命題4.4 より、
波長$\lambda$,振幅A、速さvの波は、進行方向によって
$y_1=A\sin {\left(\frac{2\pi}{\lambda}(x-vt)+\theta\right) }$(正方向に進行)
$y_2=A\sin {\left(\frac{2\pi}{\lambda}(x+vt)+\theta\right) }$(負方向に進行)
で表せる。
両者が重なるときの波形は、重ね合わせの原理から、
$y=y_1 +y_2$
$=A\sin {\left(\frac{2\pi}{\lambda}(x-vt)+\theta\right)}+A\sin {\left(\frac{2\pi}{\lambda}(x+vt)+\theta\right)}$
三角関数の加法定理(注参照)を用いて、式を計算すると、
$y=2A\cos {vt}\sin {(\frac{2\pi}{\lambda})x}$
を得る。
これは、速度0で、振幅 $2A\cos {vt}$ が時間によって変わる、波長$\lambda$の波である。
証明終わり。
(注)
定常波とその腹と節については
をみてください。</br> 定常でない波は進行波という。
干渉
2つ(以上)の波が重なり合って強めあったり弱めあったりする現象で、
波の重ね合わせの原理によって分析できる。
媒質の端における波の反射、固定端と自由端
波が媒質の終端に達するとそこで反射し、逆方向にすすむ。
固定端では、媒質は固定されているので平衡状態からの変位は生じない。
自由端では媒質は自由に動けるので、圧縮や変形をおこさない。
この条件をみたす波動方程式の解を求めると反射波を求めることができる(大学で学ぶ)。
反射した波の形は、自由端と固定端では異なる。
後続の進行波と反射波の合成波が実際に観測される波の形である。
実際に観測されるのは合成波であり、固定端では節となり、自由端では腹となる。
を参照のこと。
波面の進行にかんするホイヘンスの原理
ホイヘンスの原理
- ウィキブックス(高等学校理科 物理I 波)の1.1.1.3 ホイヘンスの原理
あるいは
を 参照のこと。</br> この原理を用いると、波面の進行の仕方が分かり、以下の反射、屈折の法則が導ける。
反射の法則
反射の法則;平面状の壁にあたった波は、反射する。この時、波の入射角と反射角は一致する。
この法則を、ホイヘンスの原理から導いてみよう。
屈折にかんするスネルの法則
この法則を、ホイヘンスの原理から導いてみよう。
回折
波がその進行方向にある障害物の背後に回り込んで伝わっていく現象のことを、回折という。
波のエネルギー
弦の振動で生じる横波の正弦波を例に、波のエネルギーを考える。
単振動のエネルギー
正弦波を固定点で観測すると、媒質の単振動が得られろ。質量m、ばね定数kの単振動する質点の力学的エネルギーは、 ${{E=K+U=\frac{1}{2}kC^2}}$ 詳しくは
- ウィキペディア(自由振動) の1.4 調和振動子のエネルギー を参照のこと。
波のエネルギー
電磁波(真空を媒質とする波)のエネルギーについては大学で学ぶ。