拘束のある問題
提供: Internet Web School
(→ラグランジュ乗数法) |
|||
| (間の43版分が非表示) | |||
| 1 行: | 1 行: | ||
==等式拘束のある問題== | ==等式拘束のある問題== | ||
| + | |||
| + | |||
| + | |||
| + | ==陰関数定理とラグランジュ乗数== | ||
| + | |||
| + | 以下の問題を考える. | ||
| + | |||
| + | |||
| + | <math>L(x,y)=x+y</math>とするとき, | ||
| + | 半径1の円周 | ||
| + | |||
| + | <math>x^2+y^2=1 \qquad (1)</math> | ||
| + | |||
| + | 上の点<math>(x,y)</math>で<math>L(x,y)=x+y</math>の最大にするものを求めよ. | ||
| + | |||
| + | |||
| + | ===関数の極値条件=== | ||
| + | |||
| + | 実数値関数<math>F(x)</math>が<math>x=x_0</math>で極小値または極大値をとり,かつ,<math>x=x_0</math>で微分可能であれば, | ||
| + | |||
| + | <math>F(x)</math>の<math>x=x_0</math>での微分係数は<math>0</math>である。 | ||
| + | |||
| + | <math>\frac{dF}{dx}(x_0) = 0</math> | ||
| + | |||
| + | |||
| + | ===陰関数=== | ||
| + | |||
| + | 半径1の円の方程式 | ||
| + | |||
| + | <math>x^2+y^2=1\qquad (1)</math> | ||
| + | |||
| + | に注目する。判りやすいように, | ||
| + | |||
| + | <math>1\ge x \ge -1,1 \ge y \ge 0</math> | ||
| + | としておく. | ||
| + | |||
| + | <math>g(x)=\sqrt{1-x^2}</math> | ||
| + | とすると, | ||
| + | <math>1\ge x \ge -1,1 \ge y \ge 0</math>では<math>(1)</math>の方程式を満たす<math>x,y</math>については | ||
| + | <math>y=g(x)</math> | ||
| + | という関係が成り立っている. | ||
| + | |||
| + | この<math>g(x)</math>という関数は,<math>(1)</math>式の中には出てこない.<math>(1)</math>からこのように間接的に導き出される関数を陰関数と呼ぶ. | ||
| + | |||
| + | |||
| + | 一般化すれば特定の条件のもとに | ||
| + | <math>f(x,y)=0</math>という式から陰関数<math>y=g(x)</math>が定義される。 | ||
| + | |||
| + | 上の例では <math>f(x,y)=x^2+y^2-1</math> | ||
| + | |||
| + | しかし,何時でも上の例のように,<math>f(x,y)=0</math>から陰関数<math>y=g(x)</math>が定義されるわけではない. | ||
| + | |||
| + | ===陰関数定理=== | ||
| + | |||
| + | ある領域D<math>\subseteq R\times R</math>で関数<math>f(x,y)</math>が連続でかつ,<math>x,y</math>について偏微分可能で, | ||
| + | その偏導関数 | ||
| + | |||
| + | <math>\frac{\partial f}{\partial x}(x,y) \qquad (1)</math> | ||
| + | |||
| + | <math>\frac{\partial f}{\partial y}(x,y) \qquad (2)</math> | ||
| + | |||
| + | も<math>(x,y)</math>について連続とする。 | ||
| + | |||
| + | D内の1点<math>(x_0,y_0)</math>で | ||
| + | |||
| + | <math>f(x_0,y_0)=0</math> | ||
| + | |||
| + | であり, | ||
| + | |||
| + | <math>\frac{\partial f}{\partial y}(x_0,y_0)\neq 0 \qquad (4)</math> | ||
| + | |||
| + | とする. | ||
| + | このとき,<math>x_0</math>を含む開区間<math>(a,b)</math>とその上の連続関数<math>g(x)</math>が存在し, | ||
| + | |||
| + | 1) 開区間<math>(a,b)</math>上で<math>f(x,g(x))=0</math> | ||
| + | |||
| + | 2) <math>y_0=g(x_0)</math> | ||
| + | |||
| + | 3) 開区間<math>(a,b)</math>上で, | ||
| + | |||
| + | <math>\frac{dy}{dx}=-\frac{\partial f / \partial x}{\partial f / \partial y} \qquad (5)</math> | ||
| + | |||
| + | |||
| + | |||
| + | 上の定理で<math>x,y</math>の役目を反対にすれば,<math>x_0=g(y_0)</math> となる陰関数の存在が示される. | ||
| + | |||
| + | ===ラグランジュ乗数法=== | ||
| + | |||
| + | |||
| + | 関数<math>L(x,y)</math>が,制約条件 | ||
| + | <math>f(x,y)=0</math> | ||
| + | の元に<math>(x,y)=(x_0,y_0)</math>で極値(極大値か極小値)をとるとする。 | ||
| + | |||
| + | <math>L(x,y)</math>が<math>(x,y)</math>について微分可能な関数で, | ||
| + | 関数<math>f(x,y)</math>は<math>(x_0,y_0)</math>が上の陰関数定理を適用できる条件を満たしているものとする。 | ||
| + | <math>x_0</math>の近傍で関数<math>g(x)</math>が存在して,<math>x_0</math>のその近傍では | ||
| + | <math>f(x,g(x))=0</math> が成り立ち,<math>y_0=g(x_0)</math>,<math>f(x_0,g(x_0))=0</math>も成り立っている. | ||
| + | <math>x,y</math>の役目を反対にすれば,<math>x_0=g(y_0)</math> となる陰関数を用いることになるが議論は全く同様に | ||
| + | できる. | ||
| + | |||
| + | |||
| + | 関数<math>L(x,y)</math>は<math>(x_0,y_0)</math>で極値(極大値か極小値)をとるから | ||
| + | <math>F(x)=L(x,g(x))</math>も<math>x=x_0</math>で極値を取る. | ||
| + | |||
| + | |||
| + | |||
| + | 極値条件により | ||
| + | |||
| + | <math>\frac{dF}{dx}(x_0)=0 \qquad (6)</math> | ||
| + | |||
| + | である. | ||
| + | |||
| + | この<math>x</math>についての微分を求めると<math>F(x)=L(x,g(x))</math>は合成関数であるから | ||
<math> | <math> | ||
| - | \frac{\partial}{\partial | + | \frac{dF}{dx}(x_0)=\frac{\partial}{\partial x}L(x_0,g(x_0))+\frac{\partial}{\partial y}L(x_0,g(x_0))\frac{d}{dx}g(x_0) \qquad (7) \\ |
| + | \frac{dy}{dx}=-\frac{\partial f / \partial x}{\partial f / \partial y} \qquad(8) | ||
</math> | </math> | ||
| + | |||
| + | <math>y=g(x)</math>であるから<math>(8)</math>式を上の<math>(7)</math>式に代入し | ||
| + | |||
| + | |||
| + | |||
| + | <math>\lambda=\frac{\partial}{\partial y}L(x_0,g(x_0))\{-\frac{\partial f}{\partial y}(x_0,g(x_0))\}^{-1} \qquad (9)</math> | ||
| + | |||
| + | という変数を使うと, | ||
| + | |||
| + | <math>0=\frac{dF}{dx}(x_0)=\frac{\partial}{\partial x}L(x_0,g(x_0))+\lambda\frac{\partial}{\partial x}f(x_0,g(x_0)) \qquad (10)</math> | ||
| + | |||
| + | また | ||
| + | |||
| + | <math>\lambda \frac{\partial}{\partial y}f(x_0,g(x_0)=-\frac{\partial}{\partial y}L(x_0,g(x)) \qquad (11)</math> | ||
| + | |||
| + | から | ||
| + | |||
| + | <math>0=\frac{\partial}{\partial y}L(x_0,g(x_0))+\lambda \frac{\partial}{\partial y}f(x_0,g(x_0)) \qquad (12) </math> | ||
| + | |||
| + | すなわち<math>\lambda</math>という新しい変数を使って | ||
| + | |||
| + | <math>H(x,y,\lambda)=L(x,y)+\lambda f(x,y) \qquad (13)</math> | ||
| + | |||
| + | という関数を造ると: | ||
| + | |||
| + | 関数<math>L(x,y)</math>が制約条件<math>f(x,y)=0</math> | ||
| + | を充たすという条件の下に | ||
| + | <math>(x,y)=(x_0,y_0)</math>で極値(極大値か極小値)をとる | ||
| + | という条件から<math>H</math>についての制約のない場合の極値条件 | ||
<math> | <math> | ||
| - | \frac{\partial}{\partial | + | \frac{\partial}{\partial x}H(x_0,y_0,\lambda)=0 \qquad (14) \\ |
| + | \frac{\partial}{\partial y}H(x_0,y_0,\lambda)=0 \qquad (15) \\ | ||
| + | \frac{\partial}{\partial \lambda}H(x_0,y_0,\lambda)=f(x_0,y_0)=0 \qquad (16) | ||
</math> | </math> | ||
| + | |||
| + | が導かれる.制約条件付きの極値問題から,<math>\lambda</math>という人工的な変数を使って | ||
| + | |||
| + | <math>目的の関数+\lambda\times (制約条件を表す関数)</math> | ||
| + | の制約条件のない場合の極値条件が導かれる. | ||
| + | |||
| + | ただしこの議論は「その点が最大(小)値を与える」<math>\Rightarrow</math> | ||
| + | 「その点が極値を与える」<math>\Rightarrow </math> 「その点での<math>微分係数=0</math>」 | ||
| + | |||
| + | |||
| + | という必要条件の連鎖であるので注意が必要である. | ||
| + | |||
| + | 「<math>微分係数=0</math>」は必要条件であるから, | ||
| + | これが満たされても,極値かどうかチェックの必要があり,さらには<math>H</math>の極値を与える<math>(x_0,y_0)</math>が求められたとしても, | ||
| + | それが最大(小)値を与えるのか確かめる必要がある。 | ||
| + | |||
| + | また,少なくとも<math>L</math>と<math>f</math>が<math>x,y</math>について微分可能であることも必要である. | ||
| + | |||
| + | ここで使われた<math>\lambda</math>はラグランジュ乗数と呼ばれる. | ||
| + | 上の問題に適用すると | ||
| + | |||
| + | |||
| + | <math>f(x,y)=x^2+y^2 -1,L(x,y)=x+y</math> | ||
| + | |||
| + | 拘束条件<math>f(x,y)=x^2+y^2 -1=0</math> を充たし,<math>L(x,y)=x+y</math>の極値を与える | ||
| + | <math>x_0,y_0</math>が存在すると仮定すれば, | ||
| + | |||
| + | <math>x_0 \neq 0</math> または <math>y_0 \neq 0</math> であり, | ||
| + | |||
| + | 陰関数の存在条件 | ||
| + | <math>\frac{\partial f}{\partial x}(x_0,y_0) = 2x_0 \neq 0 </math> | ||
| + | または | ||
| + | <math>\frac{\partial f}{\partial y}(x_0,y_0) = 2y_0 \neq 0 </math> | ||
| + | が成り立っている. | ||
| + | |||
| + | そこで, | ||
| + | |||
| + | <math>H(x,y,\lambda)=x+y+\lambda (x^2+y^2 -1)</math> | ||
| + | |||
| + | とおけば | ||
<math> | <math> | ||
| - | \frac{\partial}{\partial | + | 1+ 2\lambda x_0 = \frac{\partial}{\partial x}H(x_0,y_0,\lambda)=0 \qquad (17) \\ |
| - | \frac{\partial}{\partial | + | 1+ 2\lambda y_0 = \frac{\partial}{\partial y}H(x_0,y_0,\lambda)=0 \qquad (18) \\ |
| - | + | x_0^2+y_0^2 -1 = \frac{\partial}{\partial \lambda}H(x_0,y_0,\lambda)=0 \qquad (19) | |
| - | \frac{\partial}{\partial | + | |
</math> | </math> | ||
| + | |||
| + | |||
| + | <math>(17) </math>式から <math>\lambda \neq 0 </math> であり, | ||
| + | |||
| + | |||
| + | <math>(18),(19) </math>式から | ||
| + | |||
| + | <math>x_0 = -\frac{1}{2\lambda} ,y_0 = -\frac{1}{2\lambda}</math> | ||
| + | |||
| + | これを<math>(19)</math> 式に代入して | ||
| + | |||
| + | <math>\frac{1}{2\lambda^2} -1 = 0</math> | ||
| + | |||
| + | よって | ||
| + | |||
| + | <math>\lambda=\frac{\sqrt{2}}{2} </math> または <math>\lambda=-\frac{\sqrt{2}}{2} </math> | ||
| + | |||
| + | <math>\lambda=\frac{\sqrt{2}}{2} </math> のとき<math>x_0 = y_0= -\frac{\sqrt{2}}{2}</math> であり,<math>L(x_0,y_0)=x_0+y_0= -\sqrt{2} </math> | ||
| + | |||
| + | <math>\lambda=-\frac{\sqrt{2}}{2} </math> のとき<math>x_0 = y_0= \frac{\sqrt{2}}{2}</math> であり,<math>L(x_0,y_0)=x_0+y_0= \sqrt{2} </math> | ||
| + | |||
| + | |||
| + | 従って | ||
| + | 等式拘束条件 | ||
| + | <math>x^2+y^2=1 </math> | ||
| + | の下で<math>L(x,y)=x+y </math> の | ||
| + | 最大値は<math>x = y= \frac{\sqrt{2}}{2}</math>のときで<math>\sqrt{2} </math> | ||
| + | |||
| + | Microsoft Excel のソルバーで解くこともできる. | ||
| + | |||
| + | データの入力とソルバーのパラメータは以下の通りである.解析には非線形問題を選択する. | ||
| + | [[ファイル:LP-Fig50.1.jpg|800px]] | ||
| + | |||
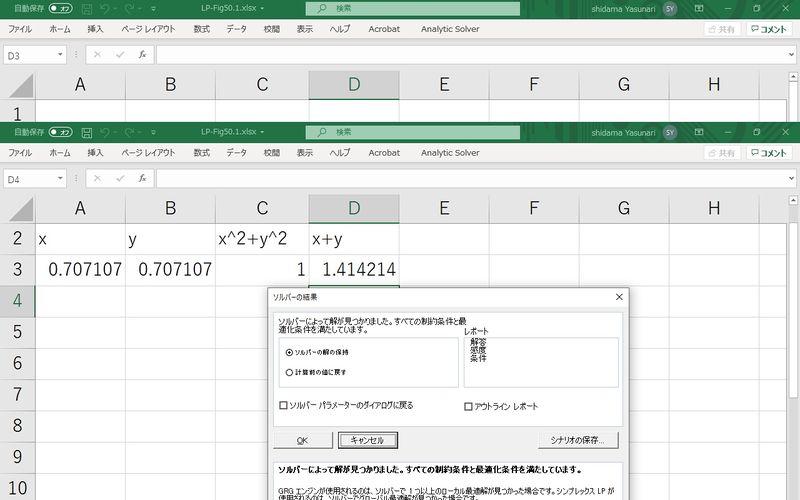
| + | ソルバーの出力は以下の通りであり前期の解析解と同じである. | ||
| + | |||
| + | [[ファイル:LP-Fig50.2.jpg|800px]] | ||
| + | |||
| + | 上記の議論を一般化したものが以下である. | ||
| + | |||
| 44 行: | 267 行: | ||
</math> | </math> | ||
| - | + | が一次独立とする.これは前項の<math>(4)</math>式の陰関数の存在条件 | |
| + | <math>\frac{\partial f}{\partial y}(x_0,y_0)\neq 0 \qquad (4)</math> | ||
| + | に相当する. | ||
| + | |||
| + | <math>m</math>個の<math>n</math>次元 | ||
| + | ベクトルからなる<math> n\times m </math>行列 | ||
| + | <math> | ||
| + | \Bigl{[} \frac{\partial g_1 }{\partial {\bf x}}(\bar{\bf x}), | ||
| + | \frac{\partial g_2 }{\partial {\bf x}}(\bar{\bf x}), | ||
| + | \cdots,\frac{\partial g_m }{\partial {\bf x}}(\bar{\bf x}) | ||
| + | \Bigr{]} | ||
| + | </math> | ||
| + | の階数が<math> m </math> であることと同値である. | ||
| + | |||
| + | |||
| + | |||
| + | このとき,一変数関数の場合と同様,以下が成立つ.すなわち, | ||
<math>m</math>次元のラグランジュ乗数ベクトル | <math>m</math>次元のラグランジュ乗数ベクトル | ||
| 62 行: | 301 行: | ||
<math> | <math> | ||
| - | \frac{\partial}{\partial x_1}\bigl{ | + | \frac{\partial}{\partial x_1}\bigl{[}l({\bf x})+\lambda_1 g_1({\bf x})+\lambda_2 g_2({\bf x})+ \cdots +\lambda_m g_m({\bf x}) \bigr{]} =0\\ |
| - | \frac{\partial}{\partial x_2}\bigl{ | + | \frac{\partial}{\partial x_2}\bigl{[}l({\bf x})+\lambda_1 g_1({\bf x})+\lambda_2 g_2({\bf x})+ \cdots +\lambda_m g_m({\bf x}) \bigr{]} =0 \\ |
\cdots \\ | \cdots \\ | ||
| - | \frac{\partial}{\partial x_n}\bigl{ | + | \frac{\partial}{\partial x_n}\bigl{[}l({\bf x})+\lambda_1 g_1({\bf x})+\lambda_2 g_2({\bf x})+ \cdots +\lambda_m g_m({\bf x})\bigr{]}=0 |
</math> | </math> | ||
| - | |||
| + | が成りたつ. | ||
==不等式拘束のある問題== | ==不等式拘束のある問題== | ||
| 81 行: | 320 行: | ||
</math> | </math> | ||
| - | を定義しておく.この(正錐)< | + | を定義しておく.この(正錐)<math>P</math>を使って,<math>{\bf p},{\bf q} \in R^m</math>の |
順序(大小)を | 順序(大小)を | ||
| 87 行: | 326 行: | ||
{\bf p} \ge {\bf q} \Leftrightarrow {\bf p} - {\bf q} \in P | {\bf p} \ge {\bf q} \Leftrightarrow {\bf p} - {\bf q} \in P | ||
</math> | </math> | ||
| + | |||
で定義する. | で定義する. | ||
| - | <math>R^n<math>から<math>R^m</math>への微分可能な写像 | + | <math>R^n</math>から<math>R^m</math>への微分可能な写像 |
<math> | <math> | ||
| 108 行: | 348 行: | ||
不等式制約 | 不等式制約 | ||
| + | |||
<math>G({\bf x}) | <math>G({\bf x}) | ||
= | = | ||
| 131 行: | 372 行: | ||
\right ) | \right ) | ||
</math> | </math> | ||
| + | |||
について,この項では以下のクーン・タッカーの条件が成立つものとする. | について,この項では以下のクーン・タッカーの条件が成立つものとする. | ||
| + | |||
| + | ===クーン・タッカーの条件=== | ||
<math> | <math> | ||
| - | G({\bf x}) \le {\bf 0} | + | G({\bf x}) \le {\bf 0} |
| - | + | ||
| - | + | ||
| - | + | ||
</math> | </math> | ||
| + | を充たす任意の<math>{\bf x} \in R^n</math>について | ||
| + | |||
| + | <math>G({\bf x})+ \frac{d G}{d {\bf x}}^T({\bf x}) {\bf k} \lt 0 </math> | ||
| + | |||
| + | となる | ||
| + | <math> {\bf k}=(k_1,k_2,\cdots,k_n)^T \in R^n</math>が存在する. | ||
ただし, | ただし, | ||
| + | |||
<math> | <math> | ||
| 163 行: | 411 行: | ||
</math> | </math> | ||
| - | <math>G({\bf x}) \le {\bf 0}< | + | ここで, |
| + | <math>G({\bf x}) \le {\bf 0}</math> | ||
は順序(大小関係)を | は順序(大小関係)を | ||
| 171 行: | 420 行: | ||
{\bf p} \ge {\bf q} \Leftrightarrow {\bf p} - {\bf q} \in P | {\bf p} \ge {\bf q} \Leftrightarrow {\bf p} - {\bf q} \in P | ||
</math> | </math> | ||
| + | |||
定義する場合, | 定義する場合, | ||
| 179 行: | 429 行: | ||
と同値になる. | と同値になる. | ||
| + | |||
| + | ===停留条件=== | ||
| + | |||
| + | 以上のクーン・タッカーの条件下で, | ||
| + | |||
微分可能な写像 | 微分可能な写像 | ||
| 189 行: | 444 行: | ||
<math>\bar{\bf x}=(\bar{x}_1,\bar{x}_2,\cdots,\bar{x}_n)</math> | <math>\bar{\bf x}=(\bar{x}_1,\bar{x}_2,\cdots,\bar{x}_n)</math> | ||
| - | + | で極小(極大)値をとるものとすると,<math>m</math>次元のラグランジュ乗数ベクトル | |
<math> | <math> | ||
| 203 行: | 458 行: | ||
</math> | </math> | ||
| - | は,<math>\bar{\bf x}=(\bar{x}_1,\bar{x}_2,\cdots,\bar{x}_n)</math> | + | は,<math>\bar{\bf x}=(\bar{x}_1,\bar{x}_2,\cdots,\bar{x}_n)</math>で極値条件(停留条件)を充たす. |
すなわち | すなわち | ||
| + | |||
<math> | <math> | ||
\frac{d l}{d {\bf x}}(\bar{\bf x})+ \frac{d G}{d {\bf x}}(\bar{\bf x}) | \frac{d l}{d {\bf x}}(\bar{\bf x})+ \frac{d G}{d {\bf x}}(\bar{\bf x}) | ||
2021年1月2日 (土) 16:44 時点における最新版
目次 |
等式拘束のある問題
陰関数定理とラグランジュ乗数
以下の問題を考える.
\(L(x,y)=x+y\)とするとき,
半径1の円周
\(x^2+y^2=1 \qquad (1)\)
上の点\((x,y)\)で\(L(x,y)=x+y\)の最大にするものを求めよ.
関数の極値条件
実数値関数\(F(x)\)が\(x=x_0\)で極小値または極大値をとり,かつ,\(x=x_0\)で微分可能であれば,
\(F(x)\)の\(x=x_0\)での微分係数は\(0\)である。
\(\frac{dF}{dx}(x_0) = 0\)
陰関数
半径1の円の方程式
\(x^2+y^2=1\qquad (1)\)
に注目する。判りやすいように,
\(1\ge x \ge -1,1 \ge y \ge 0\) としておく.
\(g(x)=\sqrt{1-x^2}\) とすると, \(1\ge x \ge -1,1 \ge y \ge 0\)では\((1)\)の方程式を満たす\(x,y\)については \(y=g(x)\) という関係が成り立っている.
この\(g(x)\)という関数は,\((1)\)式の中には出てこない.\((1)\)からこのように間接的に導き出される関数を陰関数と呼ぶ.
一般化すれば特定の条件のもとに
\(f(x,y)=0\)という式から陰関数\(y=g(x)\)が定義される。
上の例では \(f(x,y)=x^2+y^2-1\)
しかし,何時でも上の例のように,\(f(x,y)=0\)から陰関数\(y=g(x)\)が定義されるわけではない.
陰関数定理
ある領域D\(\subseteq R\times R\)で関数\(f(x,y)\)が連続でかつ,\(x,y\)について偏微分可能で, その偏導関数
\(\frac{\partial f}{\partial x}(x,y) \qquad (1)\)
\(\frac{\partial f}{\partial y}(x,y) \qquad (2)\)
も\((x,y)\)について連続とする。
D内の1点\((x_0,y_0)\)で
\(f(x_0,y_0)=0\)
であり,
\(\frac{\partial f}{\partial y}(x_0,y_0)\neq 0 \qquad (4)\)
とする. このとき,\(x_0\)を含む開区間\((a,b)\)とその上の連続関数\(g(x)\)が存在し,
1) 開区間\((a,b)\)上で\(f(x,g(x))=0\)
2) \(y_0=g(x_0)\)
3) 開区間\((a,b)\)上で,
\(\frac{dy}{dx}=-\frac{\partial f / \partial x}{\partial f / \partial y} \qquad (5)\)
上の定理で\(x,y\)の役目を反対にすれば,\(x_0=g(y_0)\) となる陰関数の存在が示される.
ラグランジュ乗数法
関数\(L(x,y)\)が,制約条件 \(f(x,y)=0\) の元に\((x,y)=(x_0,y_0)\)で極値(極大値か極小値)をとるとする。
\(L(x,y)\)が\((x,y)\)について微分可能な関数で, 関数\(f(x,y)\)は\((x_0,y_0)\)が上の陰関数定理を適用できる条件を満たしているものとする。 \(x_0\)の近傍で関数\(g(x)\)が存在して,\(x_0\)のその近傍では \(f(x,g(x))=0\) が成り立ち,\(y_0=g(x_0)\),\(f(x_0,g(x_0))=0\)も成り立っている. \(x,y\)の役目を反対にすれば,\(x_0=g(y_0)\) となる陰関数を用いることになるが議論は全く同様に できる.
関数\(L(x,y)\)は\((x_0,y_0)\)で極値(極大値か極小値)をとるから
\(F(x)=L(x,g(x))\)も\(x=x_0\)で極値を取る.
極値条件により
\(\frac{dF}{dx}(x_0)=0 \qquad (6)\)
である.
この\(x\)についての微分を求めると\(F(x)=L(x,g(x))\)は合成関数であるから
\( \frac{dF}{dx}(x_0)=\frac{\partial}{\partial x}L(x_0,g(x_0))+\frac{\partial}{\partial y}L(x_0,g(x_0))\frac{d}{dx}g(x_0) \qquad (7) \\ \frac{dy}{dx}=-\frac{\partial f / \partial x}{\partial f / \partial y} \qquad(8) \)
\(y=g(x)\)であるから\((8)\)式を上の\((7)\)式に代入し
\(\lambda=\frac{\partial}{\partial y}L(x_0,g(x_0))\{-\frac{\partial f}{\partial y}(x_0,g(x_0))\}^{-1} \qquad (9)\)
という変数を使うと,
\(0=\frac{dF}{dx}(x_0)=\frac{\partial}{\partial x}L(x_0,g(x_0))+\lambda\frac{\partial}{\partial x}f(x_0,g(x_0)) \qquad (10)\)
また
\(\lambda \frac{\partial}{\partial y}f(x_0,g(x_0)=-\frac{\partial}{\partial y}L(x_0,g(x)) \qquad (11)\)
から
\(0=\frac{\partial}{\partial y}L(x_0,g(x_0))+\lambda \frac{\partial}{\partial y}f(x_0,g(x_0)) \qquad (12) \)
すなわち\(\lambda\)という新しい変数を使って
\(H(x,y,\lambda)=L(x,y)+\lambda f(x,y) \qquad (13)\)
という関数を造ると:
関数\(L(x,y)\)が制約条件\(f(x,y)=0\) を充たすという条件の下に \((x,y)=(x_0,y_0)\)で極値(極大値か極小値)をとる という条件から\(H\)についての制約のない場合の極値条件
\( \frac{\partial}{\partial x}H(x_0,y_0,\lambda)=0 \qquad (14) \\ \frac{\partial}{\partial y}H(x_0,y_0,\lambda)=0 \qquad (15) \\ \frac{\partial}{\partial \lambda}H(x_0,y_0,\lambda)=f(x_0,y_0)=0 \qquad (16) \)
が導かれる.制約条件付きの極値問題から,\(\lambda\)という人工的な変数を使って
\(目的の関数+\lambda\times (制約条件を表す関数)\) の制約条件のない場合の極値条件が導かれる.
ただしこの議論は「その点が最大(小)値を与える」\(\Rightarrow\) 「その点が極値を与える」\(\Rightarrow \) 「その点での\(微分係数=0\)」
という必要条件の連鎖であるので注意が必要である.
「\(微分係数=0\)」は必要条件であるから, これが満たされても,極値かどうかチェックの必要があり,さらには\(H\)の極値を与える\((x_0,y_0)\)が求められたとしても, それが最大(小)値を与えるのか確かめる必要がある。
また,少なくとも\(L\)と\(f\)が\(x,y\)について微分可能であることも必要である.
ここで使われた\(\lambda\)はラグランジュ乗数と呼ばれる. 上の問題に適用すると
\(f(x,y)=x^2+y^2 -1,L(x,y)=x+y\)
拘束条件\(f(x,y)=x^2+y^2 -1=0\) を充たし,\(L(x,y)=x+y\)の極値を与える \(x_0,y_0\)が存在すると仮定すれば,
\(x_0 \neq 0\) または \(y_0 \neq 0\) であり,
陰関数の存在条件 \(\frac{\partial f}{\partial x}(x_0,y_0) = 2x_0 \neq 0 \) または \(\frac{\partial f}{\partial y}(x_0,y_0) = 2y_0 \neq 0 \) が成り立っている.
そこで,
\(H(x,y,\lambda)=x+y+\lambda (x^2+y^2 -1)\)
とおけば
\( 1+ 2\lambda x_0 = \frac{\partial}{\partial x}H(x_0,y_0,\lambda)=0 \qquad (17) \\ 1+ 2\lambda y_0 = \frac{\partial}{\partial y}H(x_0,y_0,\lambda)=0 \qquad (18) \\ x_0^2+y_0^2 -1 = \frac{\partial}{\partial \lambda}H(x_0,y_0,\lambda)=0 \qquad (19) \)
\((17) \)式から \(\lambda \neq 0 \) であり,
\((18),(19) \)式から
\(x_0 = -\frac{1}{2\lambda} ,y_0 = -\frac{1}{2\lambda}\)
これを\((19)\) 式に代入して
\(\frac{1}{2\lambda^2} -1 = 0\)
よって
\(\lambda=\frac{\sqrt{2}}{2} \) または \(\lambda=-\frac{\sqrt{2}}{2} \)
\(\lambda=\frac{\sqrt{2}}{2} \) のとき\(x_0 = y_0= -\frac{\sqrt{2}}{2}\) であり,\(L(x_0,y_0)=x_0+y_0= -\sqrt{2} \)
\(\lambda=-\frac{\sqrt{2}}{2} \) のとき\(x_0 = y_0= \frac{\sqrt{2}}{2}\) であり,\(L(x_0,y_0)=x_0+y_0= \sqrt{2} \)
従って
等式拘束条件
\(x^2+y^2=1 \)
の下で\(L(x,y)=x+y \) の
最大値は\(x = y= \frac{\sqrt{2}}{2}\)のときで\(\sqrt{2} \)
Microsoft Excel のソルバーで解くこともできる.
データの入力とソルバーのパラメータは以下の通りである.解析には非線形問題を選択する.
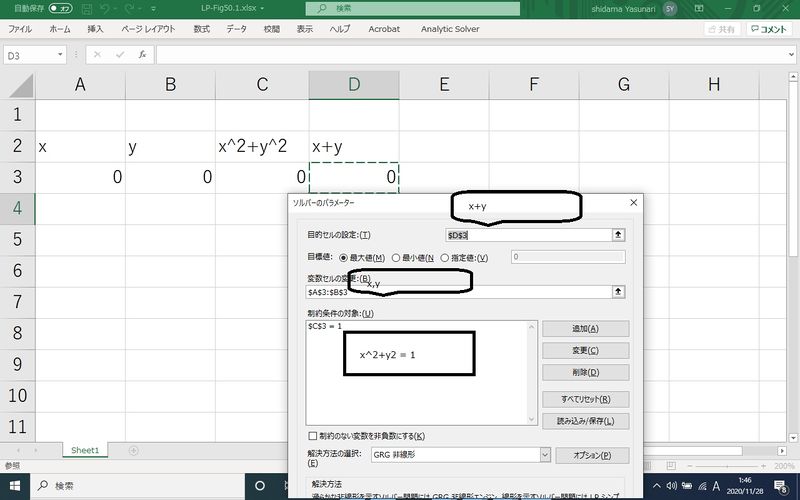
ソルバーの出力は以下の通りであり前期の解析解と同じである.
上記の議論を一般化したものが以下である.
\( l :(x_1,x_2,\cdots,x_n) \in R^n \mapsto \in R \)
が\(\bar{\bf x}=(\bar{x}_1,\bar{x}_2,\cdots,\bar{x}_n)\)で\(m\)個の制約条件
\( g_1(\bar{x}_1,\bar{x}_2,\cdots,\bar{x}_n)=0\\ g_2(\bar{x}_1,\bar{x}_2,\cdots,\bar{x}_n)=0\\ g_3(\bar{x}_1,\bar{x}_2,\cdots,\bar{x}_n)=0\\ \cdots \\ g_m(\bar{x}_1,\bar{x}_2,\cdots,\bar{x}_n)=0 \)
のもとでの極少(極大)値をとるものとする.さらに\(m\)個の\(n\)次元 ベクトル
\( \frac{\partial g_1 }{\partial {\bf x}}(\bar{\bf x})^T= \bigl{(}\frac{\partial g_1}{\partial x_1}(\bar{\bf x}),\frac{\partial g_1}{\partial x_2}(\bar{\bf x})\cdots,\frac{\partial g_1}{\partial x_n}(\bar{\bf x}) \bigr{)}\\ \frac{\partial g_2 }{\partial {\bf x}}(\bar{\bf x})^T=\bigl{(}\frac{\partial g_2}{\partial x_1}(\bar{\bf x}),\frac{\partial g_2}{\partial x_2}(\bar{\bf x})\cdots,\frac{\partial g_2}{\partial x_n}(\bar{\bf x}) \bigr{)} \\ \frac{\partial g_3 }{\partial {\bf x}}(\bar{\bf x})^T=\bigl{(}\frac{\partial g_3}{\partial x_1}(\bar{\bf x}),\frac{\partial g_3}{\partial x_2}(\bar{\bf x})\cdots,\frac{\partial g_3}{\partial x_n}(\bar{\bf x}) \bigr{)} \\ \cdots \\ \frac{\partial g_m }{\partial {\bf x}}(\bar{\bf x})^T=\bigl{(}\frac{\partial g_m}{\partial x_1}(\bar{\bf x}),\frac{\partial g_m}{\partial x_2}(\bar{\bf x})\cdots,\frac{\partial g_m}{\partial x_n}(\bar{\bf x}) \bigr{)} \\ \)
が一次独立とする.これは前項の\((4)\)式の陰関数の存在条件 \(\frac{\partial f}{\partial y}(x_0,y_0)\neq 0 \qquad (4)\) に相当する.
\(m\)個の\(n\)次元 ベクトルからなる\( n\times m \)行列 \( \Bigl{[} \frac{\partial g_1 }{\partial {\bf x}}(\bar{\bf x}), \frac{\partial g_2 }{\partial {\bf x}}(\bar{\bf x}), \cdots,\frac{\partial g_m }{\partial {\bf x}}(\bar{\bf x}) \Bigr{]} \) の階数が\( m \) であることと同値である.
このとき,一変数関数の場合と同様,以下が成立つ.すなわち, \(m\)次元のラグランジュ乗数ベクトル
\( {\bf \lambda}=(\lambda_1,\lambda_2,\cdots,\lambda_m) \) が存在し,
\( l({\bf x})+\lambda_1 g_1({\bf x})+\lambda_2 g_2({\bf x}) + \cdots +\lambda_m g_m({\bf x}) \)
は\(\bar{\bf x}=(\bar{x}_1,\bar{x}_2,\cdots,\bar{x}_n)\)で停留条件を充す.
すなわち
\( \frac{\partial}{\partial x_1}\bigl{[}l({\bf x})+\lambda_1 g_1({\bf x})+\lambda_2 g_2({\bf x})+ \cdots +\lambda_m g_m({\bf x}) \bigr{]} =0\\ \frac{\partial}{\partial x_2}\bigl{[}l({\bf x})+\lambda_1 g_1({\bf x})+\lambda_2 g_2({\bf x})+ \cdots +\lambda_m g_m({\bf x}) \bigr{]} =0 \\ \cdots \\ \frac{\partial}{\partial x_n}\bigl{[}l({\bf x})+\lambda_1 g_1({\bf x})+\lambda_2 g_2({\bf x})+ \cdots +\lambda_m g_m({\bf x})\bigr{]}=0 \)
が成りたつ.
不等式拘束のある問題
前項では,等式拘束問題を扱った.この項では不等式拘束問題を扱う. 先ず,\(R^m\)の部分集合
\( P=\{ {\bf p} |{\bf p} =(p_1,p_2,\cdots,p_m)^T \in R^m, p_1 \ge 0,p_2 \ge 0,\cdots,p_m \ge 0 \} \)
を定義しておく.この(正錐)\(P\)を使って,\({\bf p},{\bf q} \in R^m\)の 順序(大小)を
\( {\bf p} \ge {\bf q} \Leftrightarrow {\bf p} - {\bf q} \in P \)
で定義する.
\(R^n\)から\(R^m\)への微分可能な写像
\( G: {\bf x} =(x_1,x_2,\cdots,x_n) \in R^n \mapsto G({\bf x}) = \left ( \begin{array}{c} g_1({\bf x})\\ g_2({\bf x})\\ g_3({\bf x})\\ \cdots \\ g_m({\bf x}) \end{array} \right ) \in R^m \) で定義されるものとする.
不等式制約
\(G({\bf x}) = \left ( \begin{array}{c} g_1({\bf x})\\ g_2({\bf x})\\ g_3({\bf x})\\ \cdots \\ g_m({\bf x}) \end{array} \right ) \le {\bf 0}= \left ( \begin{array}{c} 0\\ 0\\ 0\\ \vdots \\ 0 \end{array} \right ) \)
について,この項では以下のクーン・タッカーの条件が成立つものとする.
クーン・タッカーの条件
\( G({\bf x}) \le {\bf 0} \) を充たす任意の\({\bf x} \in R^n\)について
\(G({\bf x})+ \frac{d G}{d {\bf x}}^T({\bf x}) {\bf k} \lt 0 \)
となる \( {\bf k}=(k_1,k_2,\cdots,k_n)^T \in R^n\)が存在する.
ただし,
\(
\frac{d G}{d {\bf x}}^T({\bf x})=
\left(
\begin{array}{cccc}
\frac{\partial g_1}{\partial x_1}({\bf x}) &
\frac{\partial g_1}{\partial x_2}({\bf x}) &
\ldots&
\frac{\partial g_1}{\partial x_m}({\bf x})\\
\frac{\partial g_2}{\partial x_1}({\bf x}) &
\frac{\partial g_2}{\partial x_2}({\bf x}) &
\ldots&
\frac{\partial g_2}{\partial x_m}({\bf x})\\
\vdots & \vdots & \vdots & \vdots \\
\frac{\partial g_m}{\partial x_1}({\bf x}) &
\frac{\partial g_m}{\partial x_2}({\bf x}) &
\cdots&
\frac{\partial g_m}{\partial x_n}({\bf x})
\end{array}
\right)
\)
ここで, \(G({\bf x}) \le {\bf 0}\) は順序(大小関係)を
\( P=\{ {\bf p} |{\bf p} =(p_1,p_2,\cdots,p_m)^T \in R^m, p_1 \ge 0,p_2 \ge 0,\cdots,p_m \ge 0 \} \\ {\bf p} \ge {\bf q} \Leftrightarrow {\bf p} - {\bf q} \in P \)
定義する場合,
\( g_1({\bf x}) \le 0 ,g_2({\bf x}) \le 0, g_3({\bf x}) \le 0, \cdots, g_m({\bf x}) \le 0 \)
と同値になる.
停留条件
以上のクーン・タッカーの条件下で,
微分可能な写像
\(
l :(x_1,x_2,\cdots,x_n) \in R^n \mapsto \in R
\)
が不等式制約\(G({\bf x}) \le {\bf 0}\) のもとで
\(\bar{\bf x}=(\bar{x}_1,\bar{x}_2,\cdots,\bar{x}_n)\) で極小(極大)値をとるものとすると,\(m\)次元のラグランジュ乗数ベクトル
\( {\bf \lambda}=(\lambda_1,\lambda_2,\cdots,\lambda_m) \ge {\bf 0} \) が存在し,
\( l({\bf x})+ G({\bf x}) {\bf \lambda} = l({\bf x})+\lambda_1 g_1({\bf x})+\lambda_2 g_2({\bf x}) + \cdots +\lambda_m g_m({\bf x}) \)
は,\(\bar{\bf x}=(\bar{x}_1,\bar{x}_2,\cdots,\bar{x}_n)\)で極値条件(停留条件)を充たす.
すなわち
\( \frac{d l}{d {\bf x}}(\bar{\bf x})+ \frac{d G}{d {\bf x}}(\bar{\bf x}) {\bf \lambda} = \left( \begin{array}{c} \frac{\partial l}{\partial x_1}(\bar{\bf x})\\ \frac{\partial l}{\partial x_2}(\bar{\bf x})\\ \vdots\\ \frac{\partial l}{\partial x_n}(\bar{\bf x})\\ \end{array} \right) + \left( \begin{array}{cccc} \frac{\partial g_1}{\partial x_1}({\bf x}) & \frac{\partial g_2}{\partial x_1}({\bf x}) & \ldots& \frac{\partial g_m}{\partial x_1}({\bf x})\\ \frac{\partial g_1}{\partial x_2}({\bf x}) & \frac{\partial g_2}{\partial x_2}({\bf x}) & \ldots& \frac{\partial g_m}{\partial x_2}({\bf x})\\ \vdots & \vdots & \vdots & \vdots \\ \frac{\partial g_1}{\partial x_n}({\bf x}) & \frac{\partial g_2}{\partial x_n}({\bf x}) & \cdots& \frac{\partial g_m}{\partial x_n}({\bf x}) \end{array} \right) \left( \begin{array}{c} \lambda_1 \\ \lambda_2 \\ \vdots \\ \lambda_m \end{array} \right) = \left ( \begin{array}{c} 0\\ 0\\ \vdots \\ 0 \end{array} \right ) \)
が成りたつ.
さらに\(\bar{\bf x}=(\bar{x}_1,\bar{x}_2,\cdots,\bar{x}_n)\)については,
\( G(\bar{\bf x}){\bf \lambda}=\lambda_1 g_1(\bar{\bf x})+\lambda_2 g_2(\bar{\bf x}) + \cdots +\lambda_m g_m(\bar{\bf x}) =0 \)
が成立つ.
\( {\bf \lambda}=(\lambda_1,\lambda_2,\cdots,\lambda_m) \ge {\bf 0} \)
は
\( \lambda_1 \ge 0,\lambda_2\ge 0,\cdots,\lambda_m \ge 0 \)
と同値になる.