線形計画法(生産計画)

提供: Internet Web School

2020年11月22日 (日) 15:54時点における版

生産計画

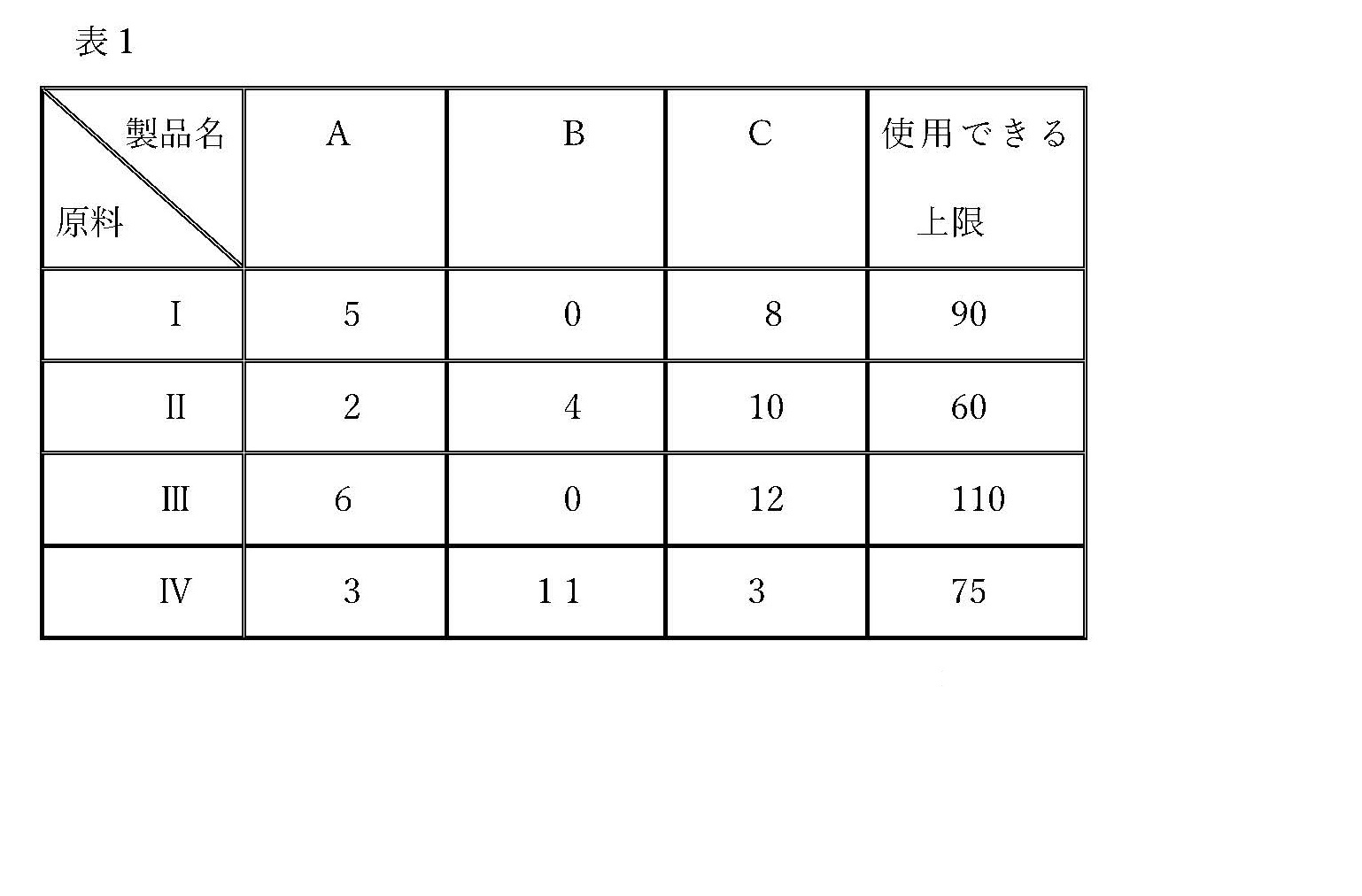
ある企業では製品A,B,Cを原料Ⅰ,Ⅱ,Ⅲ,Ⅳ用いて生産している.　製品A,B,C の1単位当たり利益をそれぞれ80,110,95とする． 　また, 製品A,B,Cを1単位生産するのに必要な原料Ⅰ,Ⅱ,Ⅲ,Ⅳのそれぞれ量と使用可能な上限が次の表で与えられる. これらの条件のもとに,利益を最大にするには製品A,B,Cをそれぞれ,どれだけ生産すれば良いか?.

この問題は以下のように数学的に定式化される．

線形計画法

製品A,B,Cをそれぞれ$x_1,x_2,x_3$ 単位生産するとき$x_1,x_2,x_3$は以下の不等式を満たす.

$4x_1+0x_2+7x_3 \leq 90 \\ 1x_1+3x_2+9x_3 \leq 60 \\ 6x_1+0x_2+14x_3 \leq 110 \\ 4x_1+10x_2+1x_3 \leq 75　\qquad (1)$

さらに各製品生産量は負ではないから

$0 \leq x_1,0 \leq x_2,0 \leq x_3 \qquad (2)$

この制約条件のもとに

$L\left(x_1,x_2, x_3 \right)=80x_1+110x_2+95x_3 \qquad (3)$

を最大にする$x_1,x_2, x_3$を求めよ.

$(1)$式のように変数に関する制約条件式が1次式で与えられ, $(3)$式のように評価関数も1次式で与えられる問題は線形計画と呼ばれる. この問題の解法にはシンプレックス法と内点法がある. シンプレクス法は[菅沼]の解説が判りやすい．

この問題を解くのにはMicrosoft Excelのソルバーや フリーソフトのOpen Office で提供されるソルバーと同等の機能をもつソフトを用いることができる.

この問題のMicrosoft Excelのソルバーによる解法例を示す。 ファイル:生産計画.pdf