最適化理論/ゲーム理論
提供: Internet Web School
(→鞍点のある問題) |
(→鞍点のある問題) |
||
| 31 行: | 31 行: | ||
を片付けるのは0点,こっそり抜け出して遊ぶ場合は100点である. | を片付けるのは0点,こっそり抜け出して遊ぶ場合は100点である. | ||
| - | + | 父親にしてみれば | |
| - | + | ||
| - | + | 「昼寝する」を選択したら,自分の失点(息子の得点)は最大100点 | |
| - | + | ||
| - | + | 「昼寝しない」選択したら,自分の失点(息子の得点)は最大50点 | |
| - | + | ||
| + | この二つの最大失点のうち最小のものは50点である. | ||
| + | |||
| + | 息子にしてみれば | ||
| + | |||
| + | 「勉強する」を選択したら自分の得点は最小-50点 | ||
| + | |||
| + | 「遊ぶ」を選択したら自分の得点は最小50点 | ||
| + | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
この二つの最小得点のうち,最大ものは50点である. | この二つの最小得点のうち,最大ものは50点である. | ||
この例では | この例では | ||
| - | + | 最大失点のうち,最小のもの」=「最小得点のうち,最大もの」 | |
が成立っている. | が成立っている. | ||
| - | + | 結局,父親が昼寝をしなければ,父親にとっては,最悪でも息子の得点は50点 | |
息子にしてみれば,「遊ぶ」を選択したら最悪でも自分の得点は50点 | 息子にしてみれば,「遊ぶ」を選択したら最悪でも自分の得点は50点 | ||
である.このような状況を「このゲームには鞍点がある」という. | である.このような状況を「このゲームには鞍点がある」という. | ||
| + | |||
この話を一般化しておく. | この話を一般化しておく. | ||
| - | 二人の競技者<math>P,Q</math> | + | |
| - | この二人がそれぞれ「戦略」の集合<math> | + | 二人の競技者<math>P,Q</math>が取り得る「戦略」の集合を<math>P_O,Q_O</math>とする.そして, |
| + | この二人がそれぞれ「戦略」の集合<math>P_O,Q_O</math>の中から戦略<math>P,Q</math>を選択したときの | ||
得点を<math>G(P,Q)</math>で表しておく. | 得点を<math>G(P,Q)</math>で表しておく. | ||
| - | 上の例では,<math>P=息子,Q=父親<math>で,<math>P_0=\{ 勉強する,遊ぶ \} <math> | + | 上の例では,<math>P=息子,Q=父親</math>で,<math>P_0=\{ 勉強する,遊ぶ \}</math> |
| - | <math>Q_0=\{ 昼寝する,昼寝しない \} | + | <math>Q_0=\{ 昼寝する,昼寝しない \} </math>である. |
| + | <math>G(P,Q)</math>は上の利得表1で与えらる. | ||
<math>P</math>が<math>P_O</math>の中から選択されると<math>Q</math>はこれに対抗して | <math>P</math>が<math>P_O</math>の中から選択されると<math>Q</math>はこれに対抗して | ||
<math>G(P,Q)</math>が最小になるように | <math>G(P,Q)</math>が最小になるように | ||
| - | + | (自分の損失が最小になるように) | |
<math>Q</math>を<math>Q_O</math>中で選択するはずである. | <math>Q</math>を<math>Q_O</math>中で選択するはずである. | ||
| + | |||
すなわち | すなわち | ||
| - | <math>\min \{ G(P,Q) |Q \in Q_O\}<math> | + | |
| + | <math>\min \{ G(P,Q) |Q \in Q_O\}</math> | ||
| + | |||
が実現されるとなるような<math>Q</math>を<math>Q_O</math>の中で探す. | が実現されるとなるような<math>Q</math>を<math>Q_O</math>の中で探す. | ||
| - | + | ||
| - | <math>\min_Q G(P,Q)</math> | + | この最小値を<math>\min_Q G(P,Q)</math> で表しておく. |
| - | + | ||
<math>P</math>はこれを見越して,自分の利益が最大になるようにするため, | <math>P</math>はこれを見越して,自分の利益が最大になるようにするため, | ||
| - | <math>\max \{ \min_Q G(P,Q) |P \in P_O\}<math> | + | |
| + | <math>\max \{ \min_Q G(P,Q) |P \in P_O\}</math> | ||
| + | |||
| + | が実現されるとなるような<math>P</math>を<math>P_O</math>の中から探すことになる. | ||
| - | |||
この最大値を | この最大値を | ||
| - | <math>\max_P \min_Q G(P,Q) <math> | + | |
| + | <math>\max_P \min_Q G(P,Q) </math> | ||
| + | |||
で表しておく. | で表しておく. | ||
| 86 行: | 99 行: | ||
<math>P</math>を<math>P_0</math>中で選択するはずである. | <math>P</math>を<math>P_0</math>中で選択するはずである. | ||
すなわち | すなわち | ||
| - | <math>\max \{ G(P,Q) |P \in P_O\}<math> | + | |
| - | が実現されるとなるような<math>P</math>を<math>P_0</math>の中から探す.この最小値を | + | <math>\max \{ G(P,Q) |P \in P_O\}</math> |
| + | |||
| + | が実現されるとなるような<math>P</math>を<math>P_0</math>の中から探す. | ||
| + | この最小値を | ||
| + | |||
<math>\min_P G(P,Q)</math> | <math>\min_P G(P,Q)</math> | ||
| + | |||
で表しておく. | で表しておく. | ||
| + | |||
<math>Q</math>はこれを見越して,自分の損失を最小にするため, | <math>Q</math>はこれを見越して,自分の損失を最小にするため, | ||
| - | <math>\min \{ \max_P G(P,Q) |Q \in Q_O\}<math> | + | |
| - | が実現されるとなるような<math>Q</math>を<math>Q_0</math>の中で探すことになる.この最大値を | + | <math>\min \{ \max_P G(P,Q) |Q \in Q_O\}</math> |
| + | |||
| + | が実現されるとなるような<math>Q</math>を<math>Q_0</math>の中で探すことになる. | ||
| + | |||
| + | この最大値を | ||
| + | |||
<math>\min_Q \max_P E(P,Q)</math> | <math>\min_Q \max_P E(P,Q)</math> | ||
| + | |||
で表しておく. | で表しておく. | ||
| 102 行: | 127 行: | ||
という関係が成り立っている. | という関係が成り立っている. | ||
| - | + | ||
| - | + | なぜばら, | |
| + | <math>Q</math>を<math>Q_O</math>の中で動かして, | ||
| + | |||
<math>\min_Q G(P,Q) \le G(P,Q)</math> | <math>\min_Q G(P,Q) \le G(P,Q)</math> | ||
| + | |||
が任意の<math>P</math>(両辺),<math>Q</math>(右辺)について成立 | が任意の<math>P</math>(両辺),<math>Q</math>(右辺)について成立 | ||
| + | |||
次に上の不等式の右辺について<math>P</math>を<math>P_0</math>中で動かして, | 次に上の不等式の右辺について<math>P</math>を<math>P_0</math>中で動かして, | ||
| - | <math>\min_Q G(P,Q) \le \max_P G(P,Q)</math> が任意の<math>P</math>(左辺),<math>Q</math> | + | |
| + | <math>\min_Q G(P,Q) \le \max_P G(P,Q)</math> | ||
| + | |||
| + | が任意の<math>P</math>(左辺),<math>Q</math> | ||
| + | |||
(右辺)について成立 | (右辺)について成立 | ||
| + | |||
さらに上の不等式の左辺について<math>P</math>を<math>P_0</math>の中で動かして, | さらに上の不等式の左辺について<math>P</math>を<math>P_0</math>の中で動かして, | ||
| - | + | ||
| - | + | <math>\max_P \min_Q G(P,Q) \le \max_P G(P,Q)</math> | |
| - | + | ||
| + | が任意の<math>Q</math>(右辺)について成立 | ||
| + | |||
| + | 最後に右辺の<math>Q</math>を<math>Q_0</math>の中で動かして | ||
| + | |||
<math> \max_P \min_Q G(P,Q) \le \min_Q \max_P G(P,Q)</math> | <math> \max_P \min_Q G(P,Q) \le \min_Q \max_P G(P,Q)</math> | ||
| - | |||
| + | である. | ||
2020年11月26日 (木) 08:30時点における版
鞍点のある問題
教育熱心な父親と,遊び盛りの息子がいる. この父親,ご多分に洩れず仕事の疲れがたまり,日曜は昼寝することが多いのですが,子煩悩で息子の勉強も気になる.
息子にしてみれば,日曜日に頼みもしないのに,父親に小言を言われながら―父親にしてみれば指導なのですが―勉強させられるのは最悪である。
鬱陶しい」が父親が起きていても,時間を稼ぎながら話題をはぐらかして,なんとか家でゲームでもした方がましと考えている.
父親が大人しく昼寝してくれて,こっそり抜け出すことができれば友人の家にでもゲームでもしに行くのだが, それができなくても,溜まった宿題を一人で片付けるほうがまだましと考えている.
父親は「昼寝をする.しない.」息子は「勉強する.遊ぶ.」でそれぞれ「戦略」に選択肢がある.
そこで,二人に「戦略」の選択によってかわる利害得失を下のように単純化して表にしてみる.
<利得表1>
\begin{tabular}{|c|c|c|} \hline &勉強する&遊ぶ \hline 昼寝しない&-50&50 \hline 昼寝する&0&100 \hline \end{tabular}
この表の値は,息子の側に立ったものである.父親が昼寝しないで「指導」を受けながら勉強する最悪な場合は得点-50点
何とか,はぐらかしながら,遊ぶ場合は
あまり楽しめないが50点,父親が昼寝して,一人で勉強して,溜まっている宿題
を片付けるのは0点,こっそり抜け出して遊ぶ場合は100点である.
父親にしてみれば
「昼寝する」を選択したら,自分の失点(息子の得点)は最大100点
「昼寝しない」選択したら,自分の失点(息子の得点)は最大50点
この二つの最大失点のうち最小のものは50点である.
息子にしてみれば
「勉強する」を選択したら自分の得点は最小-50点
「遊ぶ」を選択したら自分の得点は最小50点
この二つの最小得点のうち,最大ものは50点である.
この例では 最大失点のうち,最小のもの」=「最小得点のうち,最大もの」 が成立っている.
結局,父親が昼寝をしなければ,父親にとっては,最悪でも息子の得点は50点 息子にしてみれば,「遊ぶ」を選択したら最悪でも自分の得点は50点 である.このような状況を「このゲームには鞍点がある」という.
この話を一般化しておく.
二人の競技者\(P,Q\)が取り得る「戦略」の集合を\(P_O,Q_O\)とする.そして, この二人がそれぞれ「戦略」の集合\(P_O,Q_O\)の中から戦略\(P,Q\)を選択したときの 得点を\(G(P,Q)\)で表しておく.
上の例では,\(P=息子,Q=父親\)で,\(P_0=\{ 勉強する,遊ぶ \}\) \(Q_0=\{ 昼寝する,昼寝しない \} \)である.
\(G(P,Q)\)は上の利得表1で与えらる.
\(P\)が\(P_O\)の中から選択されると\(Q\)はこれに対抗して
\(G(P,Q)\)が最小になるように
(自分の損失が最小になるように)
\(Q\)を\(Q_O\)中で選択するはずである.
すなわち
\(\min \{ G(P,Q) |Q \in Q_O\}\)
が実現されるとなるような\(Q\)を\(Q_O\)の中で探す.
この最小値を\(\min_Q G(P,Q)\) で表しておく.
\(P\)はこれを見越して,自分の利益が最大になるようにするため,
\(\max \{ \min_Q G(P,Q) |P \in P_O\}\)
が実現されるとなるような\(P\)を\(P_O\)の中から探すことになる.
この最大値を
\(\max_P \min_Q G(P,Q) \)
で表しておく.
まっく逆の\(Q\)の立場からは, \(Q\)が\(Q_0\)の中から選択されると\(P\)はこれに対抗して \(G(P,Q)\)が最大になるように \(P\)を\(P_0\)中で選択するはずである. すなわち
\(\max \{ G(P,Q) |P \in P_O\}\)
が実現されるとなるような\(P\)を\(P_0\)の中から探す. この最小値を
\(\min_P G(P,Q)\)
で表しておく.
\(Q\)はこれを見越して,自分の損失を最小にするため,
\(\min \{ \max_P G(P,Q) |Q \in Q_O\}\)
が実現されるとなるような\(Q\)を\(Q_0\)の中で探すことになる.
この最大値を
\(\min_Q \max_P E(P,Q)\)
で表しておく.
以上出てきた,2つの値には一般には
\(\max_P \min_Q G(P,Q) \le \min_Q \max_P G(P,Q)\)
という関係が成り立っている.
なぜばら, \(Q\)を\(Q_O\)の中で動かして,
\(\min_Q G(P,Q) \le G(P,Q)\)
が任意の\(P\)(両辺),\(Q\)(右辺)について成立
次に上の不等式の右辺について\(P\)を\(P_0\)中で動かして,
\(\min_Q G(P,Q) \le \max_P G(P,Q)\)
が任意の\(P\)(左辺),\(Q\)
(右辺)について成立
さらに上の不等式の左辺について\(P\)を\(P_0\)の中で動かして,
\(\max_P \min_Q G(P,Q) \le \max_P G(P,Q)\)
が任意の\(Q\)(右辺)について成立
最後に右辺の\(Q\)を\(Q_0\)の中で動かして
\( \max_P \min_Q G(P,Q) \le \min_Q \max_P G(P,Q)\)
である.
特に「鞍点」が存在する場合,戦略\(P^* \in P_0,Q^* \in Q_O\)が存在して
\( \max_P \min_Q G(P,Q) =G(P^*,Q^*)= \min_Q \max_P G(P,Q)\)
となる.
この場合,競技者\(P,Q\)はそれぞれ戦略\(P^* \in P_0,Q^* \in Q_O\)
以外の戦略を選択すると損をすることになり,この意味で平衡状態になる.
\vspace{5cm}
\par
(図2.1 鞍点)
鞍点のない問題
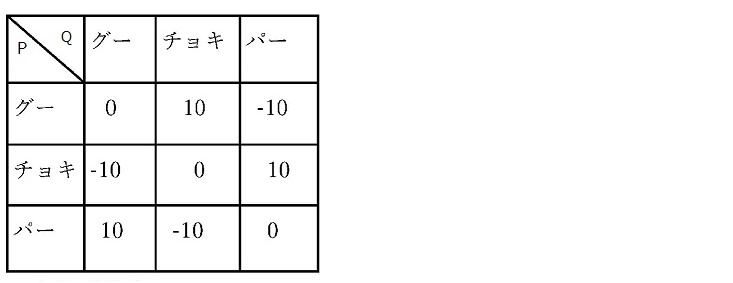
\(P,Q\)の2人がじゃんけんをする. 負けたら10円を相手に払い,勝ったら相手から10円貰うというルールで, じゃんけんを繰り返す.
無論,「アイコ」の場合は,支払うお金,貰うお金とも0円である.
\(P\)と\(Q\)の出す手によって,貰えるお金,支払うお金がどうなるか, \(P\)の立場で以下のような表になる.
「-10」は\(Q\)に10円払う事を表す. \(P\)の立場に立ってみる.先ず,このゲームの利得表には鞍点がない. 双方が選択の余地のない「平衡状態」にする戦略はないわけである.出す手をランダムしてゲームを繰り返す方法以外ない. このような問題を混合戦略問題とう. じゃんけんを繰り返すわけであるが,どのような「戦略」があるか?
グーを出し続けとすると,\(Q\)はそれを直ぐ見破って, パーを出し続けてくるであろう.続ければ続けるほど\(P\)は大損である. 同様にパーを出し続けても,チョキを出し続けるのも駄目である.
結局,例えばサイコロを用意して,出た目によって出す手を決めるランダムな手の繰り返す方法であろう.
(1か6ならグー,2か5ならパー,3か4ならチョキなど)
問題は,どんな割合で(確率で)グー,チョキ,パーを出すべきかである. 相手の\(Q\)は\(P\)の出す手を監視しながら\(P\)と対戦するので,\(P\)が選択したグー,チョキ,パーの確率を直ぐに見破り, それでも,自分にとって有利な手を選択してくると考えるべきである.\(P\)と\(Q\)の立場を替えても全く同じである.
ゲームの理論を創始し,この種の問題に解を与えたのが,ノイマン(\(von Nuemann\) 現在の計算機の原理開発者としても有名)である.
鞍点のある問題と異なり,一工夫が必要である.それは,ゲームの利得 \(G(P,Q)\)の替わりに期待値\(E(P,Q)\)を使う.以下,その説明をする.
\(P\)が選択する戦略(グー,チョキ,パーを出す確率)を\(p_1,p_2,p_3\)とし, \(P=(p_1,p_2,p_3)\)で表しておく.
このゲームの場合,「戦略」は幾つかある「手」をランダムに選んで繰り返す 確率の組み合わせになるわけである.
同様に\(Q\)が選択する戦略を\(Q=(q_1,q_2,q_3)\)で表しておく.
\(P\)がグーを出し,\(Q\)もグーを出す確率は\(p_1・q_1\)でこのとき
\(P\)は損得なし(0円の儲け),
\(P\)がグーを出し,\(Q\)がチョキを出す確率は\(p_1・q_2\) でこのとき,\(P\)は10円の儲け,
\(P\)がグーを出し,\(Q\)がパーを出す確率は\(p_1・q_3\)でこのとき, \(P\)は10円の損失(-10の儲け),
という計算を全て行うと
\(P=(p_1,p_2,p_3),Q=(q_1,q_2,q_3)\) での\(P\)の儲けの期待値\(E(P,Q)\)は
\( E(P,Q)=0・p_1・q_1+10・p_1・q_2+(-10)・p_1・q_3 +(‐10)・p_2・q_1+0・p_2・q_2+10・p_2・q_3 +10・p_3・q_1+(‐10)・p_3・q_2+0・p_3・q_3 \)
である. \(P=(p_1,p_2,p_3),Q=(q_1,q_2,q_3)\)は それぞれ,グー,チョキ,パーを出す確率を表しているから, これらについての制約は
\( 1 \ge p_1 \ge 0,1 \ge p_2 \ge 0,1 \ge p_3 \ge 0, p_1+p_2+p_3=1 \\ 1 \ge q_1 \ge 0,1 \ge q_2 \ge 0,1 \ge q_3 \ge 0, q_1+q_2+q_3=1 \)
である.
簡単のため\(P,Q\)の採り得る集合を
\( P_O= \{ (p_1,p_2,p_3)|1 \ge p_1 \ge 0,1 \ge p_2 \ge 0,1 \ge p_3 \ge 0, p_1+p_2+p_3=1\} \\ Q_O= \{ (q_1,q_2,q_3)|1 \ge q_1 \ge 0,1 \ge q_2 \ge 0,1 \ge q_3 \ge 0, q_1+q_2+q_3=1\} \)
で表しておく.前節の\(P_0,Q_0\)と異なり,それぞれ,確率を要素にもつベクトルの 集合になっている.
\(P=(p_1,p_2,p_3)\)が\(P_O\)の中から選択されると\(Q\)はこれに対抗して \(E(P,Q)\)が最小になるように (自分の損失が最小になるように) \(Q=(q_1,q_2,q_3)\)を\(Q_O\)中で選択するはずである. すなわち
\(min \{ E(P,Q) |Q \in Q_O\} \)
が実現されるとなるような\(Q\)を\(Q_O\)の中で探す. この最小値を
\(min_Q E(P,Q)\) で表しておく.
\(P\)はこれを見越して,自分の利益が最大になるようにするため,
\(max \{ min_Q E(P,Q) |P \in P_O\} \)
が実現されるとなるような\(P\)を\(P_O\)の中から探すことになる. この最大値を
\(max_P min_Q E(P,Q) \)
で表しておく.
まっく逆のQの立場からは, \(Q=(q_1,q_2,q_3)\)が\(Q_0 \)の中から選択されると\(P\)はこれに対抗して
\(E(P,Q)\)が最大になるように
\(P=(p_1,p_2,p_3)\)を\(P_0 \)中で選択するはずである. すなわち
\(max \{ E(P,Q) |P \in P_O\} \)
が実現されるとなるような\(P\)を\(P_0\)の中から探す.この最小値を \(min_P E(P,Q)\) で表しておく.
\(Q\)はこれを見越して,自分の損失を最小にするため,
\(min \{ max_P E(P,Q) |Q \in Q_O \} \) が実現されるとなるような\(Q\)を\(Q_0\)の中で探すことになる.この最大値を \(min_Q max_P E(P,Q)\) で表しておく.
以上出てきた,2つの値には一般には
\(max_P min_Q E(P,Q) \le min_Q max_P E(P,Q)\)
という関係が成り立っている.
ノイマンは上のような問題では,\(P_O,Q_0\)の中に
\(P^*=(p_1^*,p_2^*,p_3^*), Q^*=(q_1^*,q_2^*,q_3^*)\)
があって
\( max_P min_Q E(P,Q) = min_Q max_P E(P,Q)=E(P^*,Q^*) \\ max_P E(P,Q^*)=E(P^*,Q^*)= min_Q E(P^*,Q) \)
となることを証明した.
この\(P^*\)と\(Q^*\)を具体的求めることにする.
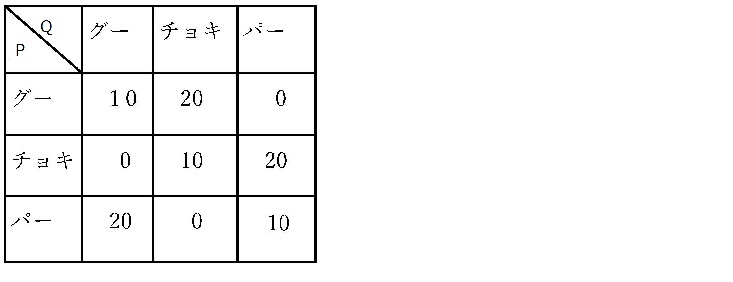
問題を解きやすくするため,最初に出てきた<利得表> (損失と利益の表)の要素に全て10を加えておく.
これでは,一方的な\(P\)のゲームになるかもしれないが,
\(P^*=(p_1^*,p_2^*,p_3^*),Q^*=(q_1^*,q_2^*,q_3^*)\)
を計算するためだけであり,このような,利得表の平行移動やっても解は同じである.
\(P^*\)も,\(Q^*\)も,\(E(P^*,Q^*)\)も未知な量であるが
\(E(P^*,Q^*)\)は判っているもの
として
\(max_P E(P,Q^*)=E(P^*,Q^*)=min_Q E(P^*,Q)\)
に注目する.
\( E(P,Q)=q_1 \{ 10p_1+0p_2+20p_3\} +q_2 \{ 20p_1+10p_2+0p_3\} +q_3 \{ 0p_1+20p_2+10p_3\} \)
で,
\(1 \ge q_1 \ge 0,1 \ge q_2 \ge 0,1 \ge q_3 \ge 0, q_1+q_2+q_3=1\)
であるので
\( E(P^*,Q^*) \le 10p_1+0p_2+20p_3~ (1) \\ E(P^*,Q^*) \le 20p_1+10p_2+0p_3~ (2) \\ E(P^*,Q^*) \le 0p_1+20p_2+10p_3~ (3) \)
という条件を満たせば,任意の\(Q \in Q_0\)について \(E(P^*,Q^*) \le E(P,Q)\) が成り立つ.従って
\(E(P^*,Q^*) \le min_Q E(P,Q)\)
が成り立つ.
\((1)\)~\((3)\)と\(P \in P_0\) 即ち
\(1 \ge p_1,p_2,p_3 \ge 0, p_1+p_2+p_3=1\)
の制約条件下で
\(E(P,Q^*)=max_P E(P,Q^*)\)となる\(P\)
を求めれば,
\(E(P,Q^*)=E(P^*,Q^*)\) となるわけである.
しかし,これではまだ\(E(P^*,Q^*)\)が未知量であるので,
\((1)\)~\((3)\)の両辺を\(E(P,Q^*)\) で割り,
\( r_1=p_1/E(P,Q^*) \\ r_2=p_2/E(P,Q^*) \\ r_3=p_3/E(P,Q^*) \)
として, \(E(P^*,Q^*)/E(P,Q^*) \ge 1\)
に注意すると
\( 1 \le 10r_1+0r_2+20r_3~(1') \\ 1 \le 20r_1+10r_2+0r_3~(2') \\ 1 \le 0r_1+20r_2+10r_3~(3') \)
\( r_1+r_2+r_3 =(p_1+p_2+p_3)/E(P,Q^*) =1/E(P,Q^*) \)
から
\(E(P,Q^*)のPについての最大化 \Leftrightarrow 「r_1+r_2+r_3の最小化」\)
結局,線形計画法の問題
\( 1 \le 10r_1+0r_2+20r_3(1') \\ 1 \le 20r_1+10r_2+0r_3(2') \\ 1 \le 0r_1+20r_2+10r_3(3') \)
かつ
\(r_1,r_2,r_3 \ge 0\)
の制約条件で
\(r_1+r_2+r_3\)
を最小化する という問題が出てくる.
Microsoft Excel のsolver などツールが利用できる.
その解から
\( p_1^*=r_1/(r_1+r_2+r_3) \\ p_2^*=r_2/(r_1+r_2+r_3) \\ p_3^*=r_3/(r_1+r_2+r_3) \)
とすれば,\(P^*\)の最適戦略が求まる.
\(P\)と\(Q\)の役目を交換しても全く同じなので,\(P^*=Q^*\)である. 最初の<利得表2>を用いれば,\(E(P^*,Q^*)\)も求まる.