提供: Internet Web School

2018年1月10日 (水) 05:15時点における版 (ソースを表示) Moderator (トーク | 投稿記録) (→　指数の有理数への拡張) ←前の差分		2018年1月10日 (水) 13:27時点における版 (ソースを表示) Moderator (トーク | 投稿記録) (→　指数の有理数への拡張) 次の差分→
267 行:		267 行:
	$\lim_{n \to \infty,n \in {\bf N}}a^n = \infty$<br/>		$\lim_{n \to \infty,n \in {\bf N}}a^n = \infty$<br/>
	を示せばよいが、これは自明である。<br/>		を示せばよいが、これは自明である。<br/>
-	③　$\lim_{\alpha \to -\infty,\alpha \in {\bf Rat}}f_a(\alpha) = \infty $ <br/>	+	③　$\lim_{\alpha \to -\infty,\alpha \in {\bf Rat}}f_a(\alpha) = 0 $ <br/>
	も、同様にして示せる。<br/>		も、同様にして示せる。<br/>
	証明終わり  $\qquad \qquad \qquad \Box$ <br/><br/>		証明終わり  $\qquad \qquad \qquad \Box$ <br/><br/>
280 行:		280 行:
	$a^{\frac{m_k}{n_k}}　\to 　a^{\frac{m}{n}}$<br/>		$a^{\frac{m_k}{n_k}}　\to 　a^{\frac{m}{n}}$<br/>
	証明<br/>		証明<br/>
		+	$|a^{\frac{m_k}{n_k}} - a^{\frac{m}{n}}| = |a^{\frac{m}{n}}| |a^{\frac{m_k}{n_k}-  \frac{m}{n}|}$ なので、<br/>
		+	$\lim_{\frac{m_k}{n_k}\to \frac{m}{n} }|a^{\frac{m_k}{n_k}-  \frac{m}{n}| = 0$<br/>
		+	を、示せばよい。<br/>
		+
		+
		+
		+
		+
		+
		+
		+	$a \gt 1$ の場合を証明する。<br/>
	====　指数の実数への拡張 ====		====　指数の実数への拡張 ====

---

2018年1月10日 (水) 13:27時点における版

目次 [非表示] 1 　８章の付録 1.1 　問の解答 1.1.1 　問 1.2 　ネイピア数　e について 1.3 　三角関数の微分 1.3.1 　準備　 1.4 指数関数と対数関数 1.4.1 　実数の累乗 1.4.1.1 　指数の整数への拡張 1.4.1.2 　指数の有理数への拡張 1.4.1.3 　指数の実数への拡張 1.4.2 　対数と対数関数 1.4.3 　対数関数 1.5 指数関数と対数関数の微分

　８章の付録

　問の解答

　問

$\lim_{n\to \infty}(1+\frac{1}{n})^n$　が存在し、２より大きく３以下であることを証明する。
（１）準備；　２項定理;を用いた展開
$a_n\triangleq (1+\frac{1}{n})^{n} \qquad (n は自然数)$ とおく。
すると、 $2 \leq a_1=1+\frac{1}{1}=2\quad \lt a_2=(1+\frac{1}{2})^{2} =2\frac{1}{4}$である。
以下に、数列　$\{a_n\}_{n=1}^{\infty}$　が単調増大で、有界（２より大、３より小）である事を示す。
するとテキストの定理により、この数列は２より大きく、３以下のある実数に収束することが分かる。
nが３以上の自然数の時は、$a_n$を２項定理を用いて展開すると
　 $a_n=(1+\frac{1}{n})^{n}=\sum_{m=0}^{n}{}_n\mathrm{C}_{m}1^{n-m}(\frac{1}{n})^m \qquad \qquad (1)$
　 ここで　${}_n\mathrm{C}_{m}$　は、ｎ個のものからｍ個取り出す取り出し方の総数で、
mが１以上でn 以下の自然数の時は
${}_n\mathrm{C}_{m}=\frac{n!}{m!(n-m)!} \qquad \qquad (2)$
ここで、m が1以上の自然数の時は　$m!\triangleq 1\cdot 2\cdot 3 \cdots (m-1)\cdot m$
mが零の時は　$\quad 0!\triangleq 1$　と定義。

すると、
${}_n\mathrm{C}_{0}=\frac{n!}{0!n!}=1\qquad \qquad (3)$　
$m \geq 1$のとき、${}_n\mathrm{C}_{m} =\frac{n!}{m!(n-m)!}=\frac{n\cdot (n-1)\cdot (n-2) \cdots \Bigl(n-(m-1)\Bigr) }{m!} \qquad (4)$
式（１）に式（２）を代入し,式(３)、(４)を利用して計算すると
$a_n = 1+\sum_{m=1}^{n}\frac{n(n-1)(n-2)\cdots \Bigl(n-(m-1)\Bigr)}{m!}1^{n-m}(\frac{1}{n})^m$
$=2+\sum_{m=2}^{n}\frac{1(1-\frac{1}{n})(1-\frac{2}{n})\cdots (1-\frac{m-1}{n})}{m!}\qquad \qquad (5)$
ここで、n　より小さい全ての自然数 i に対して
$0 \lt 1-\frac{i}{n} \lt 1$ なので、
$2 \lt a_n \lt 2+\sum_{m=2}^{n}\frac{1}{m!} \qquad \qquad \qquad (6)$

（２）すべての2以上の自然数 n　に関して、
$2 \lt a_n \lt 3 \qquad \qquad \qquad (7)$
であることを示す。
式（6）から
$2\lt a_n$,
$a_n \lt 2+\sum_{m=2}^{n}\frac{1}{m!} \qquad \qquad (8)$
右辺の　m　は2以上の自然数なので、
$\frac{1}{m!} \leq \frac{1}{(m-1)m}=\frac{1}{m-1}-\frac{1}{m}$
である。故に、
$a_n \lt 2+\sum_{m=2}^{n}(\frac{1}{m-1}-\frac{1}{m})=2+(1-\frac{1}{n})=3-\frac{1}{n}\lt 3$

（３）数列　$\{a_n\}_{n=1}^{\infty}$　は単調増加
$n \geq 2$ の時、常に　$a_n \lt a_{n+1}$　を示せばよい。
式(5)を利用すると(注参照）、
$a_{n+1}=2+\sum_{m=2}^{n+1}\frac{1(1-\frac{1}{n+1})(1-\frac{2}{n+1})\cdots (1-\frac{m-1}{n+1})}{m!}$
すると、
$a_{n+1} - a_n = \sum_{m=2}^{n+1}\frac{1(1-\frac{1}{n+1})(1-\frac{2}{n+1})\cdots (1-\frac{m-1}{n+1})}{m!} - \sum_{m=2}^{n}\frac{1(1-\frac{1}{n})(1-\frac{2}{n})\cdots (1-\frac{m-1}{n})}{m!}$
$\quad$ 右辺の第一項の和を2つに分けると、
$= \frac{1(1-\frac{1}{n+1})(1-\frac{2}{n+1})\cdots (1-\frac{n}{n+1})}{m!}$
$\quad + \sum_{m=2}^{n}\frac{1(1-\frac{1}{n+1})(1-\frac{2}{n+1})\cdots (1-\frac{m-1}{n+1})}{m!} - \sum_{m=2}^{n}\frac{1(1-\frac{1}{n})(1-\frac{2}{n})\cdots (1-\frac{m-1}{n})}{m!}$

$= \frac{ 1(1-\frac{1}{n+1})(1-\frac{2}{n+1})\cdots (1-\frac{n}{n+1}) }{m!}$
$\quad + \sum_{m=2}^{n}\frac{ 1(1-\frac{1}{n+1})(1-\frac{2}{n+1})\cdots (1-\frac{m-1}{n+1}) -1(1-\frac{1}{n})(1-\frac{2}{n})\cdots (1-\frac{m-1}{n})}{m!}$
上の式で、全ての$i\in \{1,2,,,,n\}$に対して,$(1-\frac{i}{n+1})\gt 0$と$(1-\frac{i}{n+1})\gt (1-\frac{i}{n})$　なので、
$a_{n+1} - a_n \gt 0$

（注）式（３）のｎに　ｎ＋１　を代入すればよい。

　ネイピア数　e について

定義；$e\triangleq \lim_{}(1+\frac{1}{n})^n$ をネイピア数と呼ぶ。
命題1
（１）$2 \lt e \leq 3$
（２）$e=\sum_{m=0}^{\infty}\frac{1}{m!} \qquad ただし、0!\triangleq 1,\quad m!\triangleq 1\cdot 2\cdot 3\cdots (m-1)\cdot m \qquad \qquad (9)$

　三角関数の微分

　準備　

次の命題が、三角関数の微分を求めるうえで中心的役割を果たす。　
命題２　
$\lim_{\theta\to 0,\theta\neq 0}\frac{\sin \theta}{\theta}=1$
証明
まず、$\theta$ を正に保ちながら零に近づける場合を考える。
すると、$0 \lt \theta \lt \pi/2$　と考えて良い。
点Ｏを中心にし、半径1の円を考え、円周上に一点Ａをさだめる。
図のように、円周上の点Ｂを、線分ＯＢが直線ＯＡとなす角がｘ（ラジアン)となるようにとる。

• ファイル:GENPHY00010803-01.pdf
  

図から$\triangle{OAB} \subset 扇形OAB \subset \triangle{OAP}$
$\quad$ ここで、点PはＡを通り線分OAと垂直な直線と半直線OBの交点。
すると、
$\triangle{OAB}の面積 \lt　扇形OAB の面積　\lt　\triangle{OAP}の面積$
ここで、$\triangle{OAB}の面積=\frac{1\cdot \sin{\theta}}{2},\quad 扇形OAB の面積=\pi\cdot 1^{2}\cdot \frac{\theta}{2\pi}\quad \triangle{OAP}の面積=\frac{1\cdot \tan{\theta}}{2}$なので、
$\frac{\sin{\theta}}{2}　\lt \frac{\theta}{2}\lt \frac{\tan{\theta}}{2}=\frac{\sin{\theta}}{2\cos{\theta}}\qquad$各項を2倍すると、
$\sin{\theta}\lt \theta \lt \frac{\sin{\theta}}{\cos{\theta}}$
$\quad$ここで　$\sin{\theta}\gt 0$　なので、これで上式の各項を割ると、
$1 \lt \frac{\theta}{\sin{\theta}} \lt \frac{1}{\cos{\theta}}$
$1 \gt \frac{\sin{\theta}}{\theta} \gt \cos{\theta}$
故に、極限の性質から
$1 \geq \lim_{\theta\to 0,\theta\neq 0}\frac{\sin \theta}{\theta} \geq \lim_{\theta\to 0,\theta\neq 0}\cos{\theta}=1$
これより、$\lim_{\theta\to 0,\theta\neq 0}\frac{\sin \theta}{\theta}=1$　が得られる。

定理１　三角関数の微分
（１）$\frac{d}{d\theta}\sin{\theta}=\cos{\theta}$
（２）$\frac{d}{d\theta}\cos{\theta}=-\sin{\theta}$
証明
（１）；　$\frac{d}{d\theta}\sin{\theta} \triangleq \lim_{h\to 0,h\neq 0}\frac{\sin (\theta+h)-\sin \theta}{h}$
ここで、
$\sin (\theta+h)-\sin \theta = \sin \bigl((\theta + \frac{h}{2})+\frac{h}{2}\bigr) - \sin \bigl((\theta + \frac{h}{2})-\frac{h}{2}\bigr)$
サイン関数の加法定理を適用すると
$=\sin (\theta + \frac{h}{2})\cos \frac{h}{2} + \cos (\theta + \frac{h}{2})\sin \frac{h}{2} - \Bigl( \sin (\theta + \frac{h}{2})\cos \frac{h}{2} - \cos (\theta + \frac{h}{2})\sin \frac{h}{2} \Bigr) = 2\cdot \cos (\theta + \frac{h}{2})\sin \frac{h}{2}$
故に、 $\frac{d}{d\theta}\sin{\theta} \triangleq \lim_{h\to 0,h\neq 0}\frac{\sin (\theta+h)-\sin \theta}{h} = \lim_{h\to 0,h\neq 0}\frac{2\cdot \cos (\theta + \frac{h}{2})\sin \frac{h}{2}}{h}=\lim_{h\to 0,h\neq 0}\cos (\theta + \frac{h}{2})\frac{\sin \frac{h}{2}}{h/2}$
$=\lim_{h\to 0,h\neq 0}\cos (\theta + \frac{h}{2})\lim_{h\to 0,h\neq 0}\frac{\sin \frac{h}{2}}{h/2}$
$\quad$ ここで、
$\quad \lim_{h\to 0,h\neq 0}\cos (\theta + \frac{h}{2}) = \cos \theta$
$\quad \lim_{h\to 0,h\neq 0}\frac{\sin \frac{h}{2}}{h/2} = 1 \quad (上の命題２より）$
$\quad$なので、
$=\cos \theta$

指数関数と対数関数

　実数の累乗

$a$ を任意の実数、$n$　を2以上の自然数とする。
$a^1=a,\quad a^2=a\cdot a,\quad a^3=a^2\cdot a=a\cdot a\cdot a ,\quad \cdots \quad a^n=a^{n-1}\cdot a,　\cdots$
を総称して、a　の累乗と呼ぶ。
$a^n$　を$a$ の n 乗 、$n$　をその指数と呼ぶ。
この累乗が次のような計算規則を満たすことは、容易に証明できる。
命題１
$a,b$　を任意の実数、$m, n$ を任意の自然数とすると、
(1)　$a^{m}a^{n} = a^{m+n}$
(2)　$(a^{m})^n =a^{m n}$
(3)　$(ab)^n = a^n b^n$

そこで次の累乗に関する計算規則を定義する。

累乗に関する計算規則
$a, b$　を任意の正の実数、$\alpha,\quad \beta$を指数を表わす数とすると、
(1)　$a^{\alpha}a^{\beta} = a^{\alpha+\beta} \qquad \qquad \qquad (累乗規則１)$
(2)　$(a^{\alpha})^\beta =a^{\alpha \beta} \qquad \qquad \qquad (累乗規則２)$
(3)　$(ab)^\beta = a^\beta b^\beta \qquad \qquad \qquad (累乗規則３)$

この計算規則(3)から、$1^\beta \equiv 1$　であることが分かる。
何故ならば　$b=1$の時、$(a・1)^\beta = a^\beta 1^\beta$　となり、 $a^\beta \neq 0$　であるから。
そこで今後は $a \neq 1$　の場合だけを考える。

命題２
（１）$a$　を1より小さい正の実数とすると、数列　$\{a^{n}\}_{n=1}^{\infty}$　は単調減少し、零に収束。
（２）$a$　を1より大きい正の実数とすると、数列　$\{a^{n}\}_{n=1}^{\infty}$　は単調増加し、いくらでも大きくなる（無限大に発散）。

これより、累乗に関する３つの規則が、そのまま成り立つようにしながら、指数を実数まで拡げよう。

　指数の整数への拡張

まず指数を、累乗に関する３つの規則が成り立つようにしながら、整数に拡張する。
累乗の定義から、
$a \neq 0,1$　の時は、任意の自然数ｍ、ｎに対し、
$a^m \div a^n = a^{m-n} \qquad (m\gt n)　\qquad \qquad (1)$
$\qquad \qquad = 1 \qquad (m = n)\qquad \qquad \qquad(2)$
$\qquad \qquad = \frac{1}{a^{n-m}} \qquad (m \lt n)\qquad \qquad (3)$
であることが分かる。
これを一つの式　$a^{m-n}$　で表わせるように、a　の指数を取決めたい。
そのためには、指数が零の時、$a^0 \triangleq 1$、
指数　$m-n$　が負数の時　$a^{m-n} \triangleq \frac{1}{a^{n-m}}$　
と定義すればよい。
言い換えると、$a (\neq 0,1)$　の指数ｎが 零と負の整数のとき、
$a^0 \triangleq 1, \qquad a^n \triangleq \frac{1}{a^{-n}} \qquad (n\lt 0)\qquad \qquad (4)$
と定義する。
すると、指数が整数の時、３つの累乗規則を満たすことは、容易に確かめられる。

　指数の有理数への拡張

これ以降、有理数全体のなす集合を${\bf Rat}$とかく。
$a (\neq 1)$　を任意の正の実数、　$\frac{m}{n}$　を任意の有理数のとき、
$a$　の有理数乗　$a^{\frac{m}{n}}$　を、計算規則を満たすように定義しよう。

指数n　を任意の自然数（正の整数）、 m　を任意の整数と仮定してよい。
$\qquad$（注）nが負の時は$a^{\frac{m}{n}} = a^{\frac{-m}{-n}}$　なので、
$\qquad \quad -n,-m$を改めて$n,m$ と置けば良い。$\Box$
累乗規則（２）を満たすように定義するには、
$(a^{\frac{m}{n}})^{n} = (a^{\frac{m}{n}})^{\frac{n}{1}} = a^{m}$　
でなければならない。
これは、$a^{\frac{m}{n}}$　が　$a^{m}$　のｎ乗根であることを示す。
しかしｎが偶数のときは、$-a^{\frac{m}{n}}$ も$a^{m}$　のｎ乗根となるので、 正のｎ乗根　のほうを、$a^{\frac{m}{n}}$　とかく。

定義　正の実数の有理数乗
$a$を正の実数とする。
$a^{\frac{m}{n}}$　とは、
$a^{m}$　の正のｎ乗根である。
すなわち、　
$(a^{\frac{m}{n}})^{n} =a^{m}$を満たす正の実数である。

最初に、この定義できちんと正の実数が一つだけ決まることを証明しよう。
$a=1$のときは、ｎ乗すると１になる正数は１だけなので
$1^{\frac{m}{n}})=1$
であることが分かるので、$a \neq 1$　の場合を考える。
命題３
$a \neq 0,1$　を任意の正の実数、$m$　を任意の整数,$n$を任意の自然数とする。
すると、n 乗すると　$a^{m}$　になる正の実数 $b$ (i.e. $\quad b^n = a^{m}$)が存在し、ただ一つに限る。
証明
(1) 存在性
$f(x) \triangleq x^n$　という、零と正の実数の上で定義された、関数を考える。
この関数はｘが増加するにつれて、連続的に、零から正の無限大に狭義に単調に増加（注参照）していく。
そこで、$B\triangleq \{x \in [0,\infty)\ |\ x^n \leq a^{m} \}$ という集合を考える。
この集合は、上に有界な区間になり、実数の連続性から上限(sup)$b$を持つ。
この時、$b \in B, \quad b^n = a^{m}$ であることを示そう。
$b$　が集合$B (\in {\bf R})$の上限なので、任意の自然数ｎに対して、
$0 \leq b - b_{n} \lt \frac{1}{n}$ 　
を満たす　$b_{n} \in B$ が存在する。
明らかに
$\lim_{n \to \infty}b_{n} = b$
すると、関数　$f(x) \triangleq x^n$　は連続なので、 $\lim_{n \to \infty}b_{n}^n = b^n \qquad \qquad \qquad (a)$
ところが$b_{n} \in B \triangleq \{x \in [0,\infty)|x^n \leq a^{m} \}$なので、
$b_{n}^n \leq a^{m} \qquad \qquad \qquad (b)$
式(a)、(b)　から、$b^n \leq a^{m}$　がえられるので、
$b \in B$
が示せた。（従って、Bは閉区間　[o,b]　である。）
$b^n = a^{m}$　であることを背理法を使って示そう。
もし、$b^n \lt a^{m}$　だとすると、関数　$f(x) = x^n$　は連続なので
充分小さな正の実数$\delta$ をとると、$(b + \delta) ^n \lt a^{m}$ を満たす。
すると　$(b + \delta) \in B$　となり、
$b$が B の上限であることに矛盾してしまう。
故に、背理法により、$b^n = a^{m}$　が証明できた。
（２）一意性
関数　$f(x) = x^n$ 　は狭義の単調増加関数なのでｂ以外の数ｂ'($\neq b$)では、
${b'}^n \neq b^n =a^m$
（証明終り）　$\qquad \qquad \Box$
(注)　関数ｆが狭義単調増加とは、$x \lt y \Rightarrow f(x) \lt f(y)$　を満たすこと。

命題４
任意の正の実数　$a \neq 1$ にたいして、その有理数乗を上記のように定義すると
３つの累乗規則　(1)～(3)　が成り立つ。
証明； １）　累乗規則（１)が成り立つことを示す。
2個の有理数の指数を　自然数$n,\quad \tilde{n}$と整数$m,\quad \tilde{m}$　を用いて、
$\alpha = \frac{m}{n},\quad \beta = \frac{\tilde{m}}{\tilde{n}}$と表現する。
すると、累乗規則（１)は、次のように表される。
$a^{\frac{m}{n}}a^{\frac{\tilde{m}}{\tilde{n}}} = a^{\frac{m}{n}+\frac{\tilde{m}}{\tilde{n}}}$
この左辺を　$b \triangleq a^{\frac{m}{n}}a^{\frac{\tilde{m}}{\tilde{n}}}$,
右辺を　$c \triangleq a^{\frac{m}{n}+\frac{\tilde{m}}{\tilde{n}}}$　とおく。
$b^{n \tilde{n}} = c^{n \tilde{n}} 　\qquad \qquad \qquad (a)$　
であることを示せば、$b = c$ が得られ,
累乗規則（１)が成立することが分かる。
まず左辺を考える。
$b^{n \tilde{n}} =　(a^{\frac{m}{n}}a^{\frac{\tilde{m}}{\tilde{n}}})^{n \tilde{n}}$
指数が自然数の累乗規則（３）から
$= (a^{\frac{m}{n}})^{n \tilde{n}}(a^{\frac{\tilde{m}}{\tilde{n}}})^{n \tilde{n}}$
指数が自然数の累乗規則（２）から
$= \Bigl((a^{\frac{m}{n}})^{n}\Bigr)^{\tilde{n}}\Bigl((a^{\frac{\tilde{m}}{\tilde{n}}})^{\tilde{n}}\Bigr)^{n}$
実数の有理数乗の定義から、
$= (a^{m})^{\tilde{n}}(a^{\tilde{m}})^{n}$
指数が整数の累乗規則（２）から
$= a^{m \tilde{n}}a^{\tilde{m}n}$
指数が整数の累乗規則（１）から
$= a^{m \tilde{n} + \tilde{m}n}$
故に、$b^{n \tilde{n}} = a^{m \tilde{n} + \tilde{m}n}$
次に、右辺を考える。
$c^{n \tilde{n}} = (a^{\frac{m}{n}+\frac{\tilde{m}}{\tilde{n}}})^{n \tilde{n}}$

$= (a^{ \frac{m\tilde{n}+n\tilde{m}}{n\tilde{n}}})^{n \tilde{n}}$
実数の有理数乗の定義から、
$= a^{m\tilde{n} + n\tilde{m}} = b^{n \tilde{n}}$
これで、式（a)が示され、累乗規則（１)が成り立つことが証明できた。
　 ２）累乗規則（２)と累乗規則（３)が成り立つことは読者がしてください。
証明終わり。

指数が有理数の場合,命題２は次のように拡張出来る。

命題５
${\bf Rat}$の上で定義される関数
$f_a(\alpha) \triangleq a^{\alpha}　\qquad (\alpha \in {\bf Rat})$を考える。
１）$a$　を1より大きい正の実数とすると、
$f_a$は単調増大で
$\lim_{\alpha \to \infty,\alpha \in {\bf Rat}}a^{\alpha} = \infty　\quad \lim_{\alpha \to -\infty}f_a(\alpha) = 0$
２）$a$　が1より小さい正の実数のとき、
$f_a$は単調減少し、
$\lim_{\alpha \to \infty,\alpha \in {\bf Rat}}f_a(\alpha) = 0\quad \lim_{\alpha \to -\infty,\alpha \in {\bf Rat}}f_a(\alpha) = \infty$
３）$a = 1$　のとき、$f_a　\equiv　1$
証明
１）のみ証明する。２)の場合も同様に証明できる。
①　$\frac{m}{n} \lt \frac{m'}{n'} ,\quad n,m \in {\bf N}$　とすると、
$a^{\frac{m}{n}} \lt a^{\frac{m'}{n'}}$ を示そう。
$\alpha \triangleq a^{\frac{m'}{n'}} \div a^{\frac{m}{n}} \gt 1$
を示せばよい。
正数の有理数乗の計算規則から、
$\alpha \triangleq a^{\frac{m'}{n'}} \div a^{\frac{m}{n}}=a^{\frac{m'}{n'}-\frac{m}{n}}$
$=a^{ \frac{m'n-n'm}{n'n} }$
故に、
${\alpha}^{n'n} = a^{m'n-n'm}$
$\qquad \frac{m}{n} \lt \frac{m'}{n'}$　から、
$\qquad m'n-n'm \gt 0$なので、$a^{m'n-n'm} \gt 1$であり
$\gt 1$
故に、　${\alpha}^{n'n} \gt 1$
自然数乗すると１より大きくなる正の実数は１より大きい実数しかないので、 $\alpha \gt 1$　が得られた。
②　$\lim_{\alpha \to \infty,\alpha \in {\bf Rat}}a^{\alpha}= \infty$を示そう。
関数　$f_a(\alpha)$　は単調増加（①で証明)なので、
$\lim_{n \to \infty,n \in {\bf N}}a^n = \infty$
を示せばよいが、これは自明である。
③　$\lim_{\alpha \to -\infty,\alpha \in {\bf Rat}}f_a(\alpha) = 0$
も、同様にして示せる。
証明終わり $\qquad \qquad \qquad \Box$

定理１
$a \neq 0,1$ の正の実数とする。
有理数全体の上で定義される(単調)関数
$f_a(\alpha) \triangleq a^{\alpha}　\qquad (\alpha は有理数)$
は連続関数である。
すなわち、
$\frac{m_k}{n_k}\to \frac{m}{n} \quad ({\bf N} \ni k\to \infty) \quad (m_k,m は整数、 n_k,n　は自然数）$
ならば、
$a^{\frac{m_k}{n_k}}　\to 　a^{\frac{m}{n}}$
証明
$|a^{\frac{m_k}{n_k}} - a^{\frac{m}{n}}| = |a^{\frac{m}{n}}| |a^{\frac{m_k}{n_k}- \frac{m}{n}|}$ なので、
$\lim_{\frac{m_k}{n_k}\to \frac{m}{n} }|a^{\frac{m_k}{n_k}- \frac{m}{n}| = 0$
を、示せばよい。

$a \gt 1$ の場合を証明する。

　指数の実数への拡張

任意の実数　$\alpha$　に対して　指数　$a^{\alpha}$　を次のように定義する。

定義
$\{\alpha_n\}_{n=1}^{\infty}$ を　$\alpha$　に収束する有理数の単調増加数列とするとき、
$a^{\alpha} \triangleq \lim_{n \to \infty}a^{\alpha_{n}}$　

この定義により、唯一の実数が必ず定まることが次のようにして分かる。

命題６
$\alpha$　に収束する別の有理数の単調増加数列　$\{\beta_n\}_{n=1}^{\infty}$　に対して、
$\lim_{n \to \infty}a^{\beta_{n}} = \lim_{n \to \infty}a^{\alpha_{n}}$　
証明
証明終わり

定理２
$a \neq 0,1$　である正の実数$a$を考える。
実数空間　${\bf R}$ で定義された指数関数
$f_{a}(x)= a^x　\quad (x \in {\bf R})$　
は、次の性質をもつ。
（１）$(0,\infty)$　の上への、一対一関数
（２）$a \gt 1$　ならば単調増加、$\quad a \lt 1$　ならば単調減少
（３）連続関数

　対数と対数関数

1と異なる正の実数　$a$　を考える。
指数関数　$f_{a}(x) = a^x$ は,命題２から、
${\bf R}$　から　$(0,\infty)$　の上への、一対一、連続関数である。

　 定義１
実数　$a$ を　$a\gt 0,\ a\neq 1$　とする。この時、
任意の正の実数　Xに対して、
$a^x = X$
を満たす実数ｘが唯一つ定まる。
このｘを　X　の$a$　を底とする対数と呼び、$\log_{a}X$ とかく。

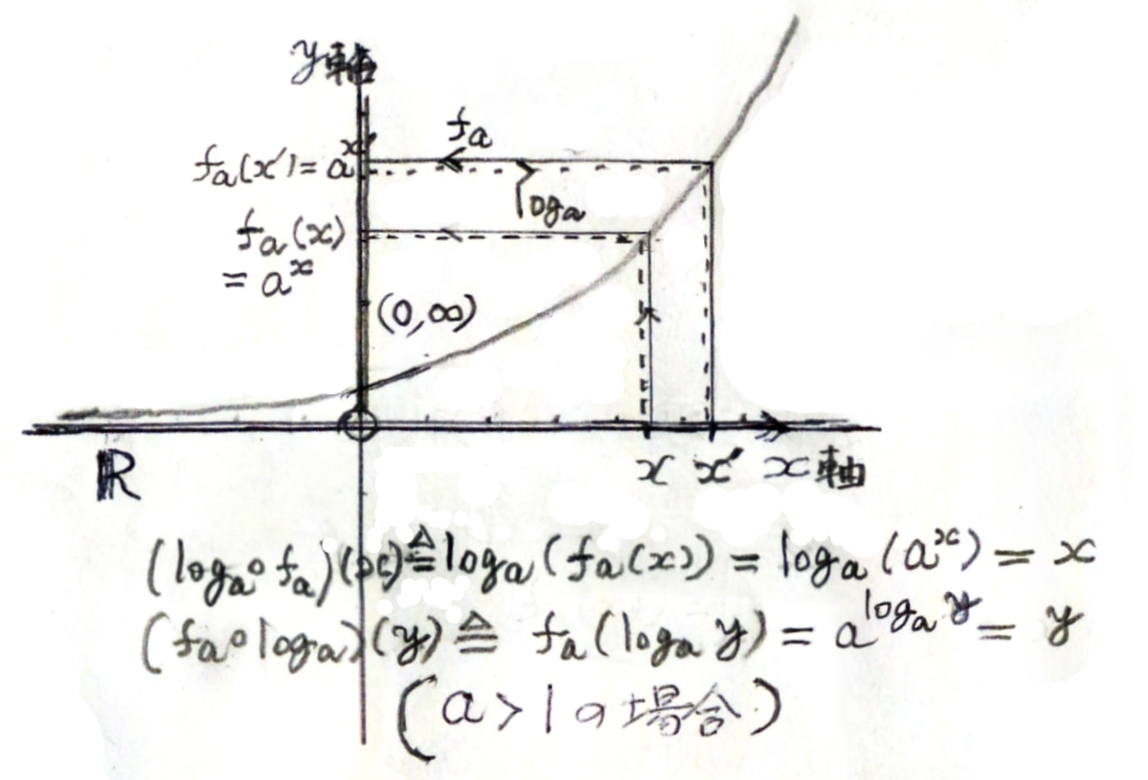
指数関数　$f_{a}(x) = a^x$ は
${\bf R}$　から　$(0,\infty)$　の上への、一対一関数
なので、逆関数を考えることができる。

• ファイル:GENPHY00010804-01.pdf　
• 　

定義２
$a$　を1と異なる正の実数とする。
$\log_{a} a^x \triangleq x \qquad \qquad \qquad (1)$　
この関数を、$a$ を底とする対数関数とよぶ。

　 定理１
$a$　を　1と異なる正の実数とする。
１）　$a$ を底とする対数関数　$\log_{a}$　は、
指数関数$f_{a}(x)=a^x$の逆関数であり、
$(\log_{a}\cdot f_{a})(x) = x \quad (x \in {\bf R})\qquad \qquad \qquad (2)$
すなわち、
$\log_{a}(a^x) = x \quad (x \in {\bf R})\qquad \qquad \qquad (2')$
と(注参照)、
$(f_{a}\cdot \log_{a})(y) = y \quad \bigl(y \in (0,\infty)\bigr)\qquad \qquad \qquad (3)$
すなわち、
$a^{\log_{a}(y)} = y \quad \bigl(y \in (0,\infty)\bigr)\qquad \qquad \qquad (3')$
を満たす。
２）指数関数$f_{a}(x)=a^x$　は
$(0,\infty)$　から　${\bf R}$　の上への一対一で
連続な関数である。
(注)　2つの関数f、ｇに対して、その合成関数$(f\cdot g)$　は、
$(f\cdot g)(x)\triangleq f\bigl(g(x)\bigr)$　で定義される。

定理２
$a$　を　1と異なる正の実数とする。
すると
1)　任意の2つの正の実数ｂ、ｃに対して,
$\qquad \log_{a}b + \log_{a}c = \log_{a}bc \qquad \qquad \qquad (4)$
2)　任意の2つの正の実数 b,c に対して,
$\qquad \log_{a}b - \log_{a}c = \log_{a}\frac{b}{c} \qquad \qquad \qquad (5)$
3)　任意の正の実数 b と任意の実数 c に対して　
$\qquad \log_{a}b^c = c \log_{a}b \qquad \qquad \qquad (6)$

証明
1)　指数関数$f_{a}(x)=a^x$ の性質から、
$a^{x_{b}}= b,\quad a^{x_{c}}= c \qquad \qquad \qquad (7)$　
を満たす、実数 $x_{b} \quad x_{c}$ がそれぞれ唯一つ定まる。
式(7)から対数関数の定義を用いると、
$\log_{a}b = x_{b} \quad \log_{a}c = x_{c}\qquad \qquad \qquad (8)$　
すると、
$\quad \log_{a}b + \log_{a}c = x_b + x_c \quad (式(8)から)$
$=\log_{a} a^{x_b + x_c } \quad (式(1)から)$
$=\log_{a} (a^{x_b} a^{x_c }) \quad (指数関数の性質から)$
$=\log_{a}(bc) \quad (式(7)から)$

2)も同様に証明できる。

３）$X \triangleq \log_{a}b^c$ とおく。すると、対数の定義から、
$a^X = b^c$
$\qquad$ ｂは正の実数なので、$x_b=\log_{a}b　とおくと、 a^{x_b}= b$なので、
$= (a^{x_b})^c = a^{x_b c} \quad (指数関数の性質から）$
故に
$a^X = a^{x_b c}$
指数関数が一対一関数なので、$X = x_b c = c \log_{a}b$
X の定義から、$\log_{a}b^c = c \log_{a}b \qquad \qquad \Box$

定理３　底の変換公式
任意の3つの正の実数　$a(\neq 1),b,c(\neq 1)$　に対して
$\qquad \log_{a}b = \frac{\log_{c}b}{\log_{c}a}\qquad \qquad \qquad (9)$

証明
定理１の式(3')から、
$\quad a^{\log_{a}b} = b \qquad \qquad \qquad (10)$
底をｃとする対数をとれば、
$\log_{c}a^{\log_{a}b} = \log_{c} b$
$\qquad$定理２の式(6)から、$\log_{c}a^{\log_{a}b} = (\log_{a}b)(\log_{c}a)$なので、
$(\log_{a}b)(\log_{c}a) = \log_{c} b$
$a,\quad c$ は、１と異なる正の実数であるため、$\log_{c}a \neq 0$　となり、
$\log_{a}b = \frac{\log_{c}b }{\log_{c}a}$
が得られた。
証明終わり。 $\qquad \qquad \qquad \Box$

　対数関数

1と異なる正の実数　$a$　を考える。
　 指数関数　$f_{a}(x) = a^x$ は,命題２から、
　 ${\bf R}$　から　$(0,\infty)$　の上への、一対一、連続関数である。
　 すると、その逆関数$\quad (0,\infty) \ni a^x \to x \in {\bf R}$　が定義できる。

• ファイル:GENPHY00010804-01.pdf　
• 　

定義
$a$　を1と異なる正の実数とする。
$\log_{a} a^x \triangleq x \qquad \qquad \qquad (1)$　
この関数を、$a$ を底とする対数関数とよぶ。

　 定理１
$a$　を　1と異なる正の実数とする。
１）　$a$ を底とする対数関数　$\log_{a}$　は、
指数関数$f_{a}(x)=a^x$の逆関数であり、
$(\log_{a}\cdot f_{a})(x) = x \quad (x \in {\bf R})\qquad \qquad \qquad (2)$
すなわち、
$\log_{a}(a^x) = x \quad (x \in {\bf R})\qquad \qquad \qquad (2')$
と(注参照)、
$(f_{a}\cdot \log_{a})(y) = y \quad \bigl(y \in (0,\infty)\bigr)\qquad \qquad \qquad (3)$
すなわち、
$a^{\log_{a}(y)} = y \quad \bigl(y \in (0,\infty)\bigr)\qquad \qquad \qquad (3')$
を満たす。
２）指数関数$f_{a}(x)=a^x$　は
$(0,\infty)$　から　${\bf R}$　の上への一対一で
連続な関数である。
(注)　2つの関数f、ｇに対して、その合成関数$(f\cdot g)$　は、
$(f\cdot g)(x)\triangleq f\bigl(g(x)\bigr)$　で定義される。

定理２
$a$　を　1と異なる正の実数とする。
すると
1)　任意の2つの正の実数ｂ、ｃに対して,
$\qquad \log_{a}b + \log_{a}c = \log_{a}bc \qquad \qquad \qquad (4)$
2)　任意の2つの正の実数 b,c に対して,
$\qquad \log_{a}b - \log_{a}c = \log_{a}\frac{b}{c} \qquad \qquad \qquad (5)$
3)　任意の正の実数 b と任意の実数 c に対して　
$\qquad \log_{a}b^c = c \log_{a}b \qquad \qquad \qquad (6)$

証明
1)　指数関数$f_{a}(x)=a^x$ の性質から、
$a^{x_{b}}= b,\quad a^{x_{c}}= c \qquad \qquad \qquad (7)$　
を満たす、実数 $x_{b} \quad x_{c}$ がそれぞれ唯一つ定まる。
式(7)から対数関数の定義を用いると、
$\log_{a}b = x_{b} \quad \log_{a}c = x_{c}\qquad \qquad \qquad (8)$　
すると、
$\quad \log_{a}b + \log_{a}c = x_b + x_c \quad (式(8)から)$
$=\log_{a} a^{x_b + x_c } \quad (式(1)から)$
$=\log_{a} (a^{x_b} a^{x_c }) \quad (指数関数の性質から)$
$=\log_{a}(bc) \quad (式(7)から)$

2)も同様に証明できる。

３）$X \triangleq \log_{a}b^c$ とおく。すると、対数の定義から、
$a^X = b^c$
$\qquad$ ｂは正の実数なので、$x_b=\log_{a}b　とおくと、 a^{x_b}= b$なので、
$= (a^{x_b})^c = a^{x_b c} \quad (指数関数の性質から）$
故に
$a^X = a^{x_b c}$
指数関数が一対一関数なので、$X = x_b c = c \log_{a}b$
X の定義から、$\log_{a}b^c = c \log_{a}b \qquad \qquad \Box$

定理３　底の変換公式
任意の3つの正の実数　$a(\neq 1),b,c(\neq 1)$　に対して
$\qquad \log_{a}b = \frac{\log_{c}b}{\log_{c}a}\qquad \qquad \qquad (9)$

証明
定理１の式(3')から、
$\quad a^{\log_{a}b} = b \qquad \qquad \qquad (10)$
底をｃとする対数をとれば、
$\log_{c}a^{\log_{a}b} = \log_{c} b$
$\qquad$定理２の式(6)から、$\log_{c}a^{\log_{a}b} = (\log_{a}b)(\log_{c}a)$なので、
$(\log_{a}b)(\log_{c}a) = \log_{c} b$
$a,\quad c$ は、１と異なる正の実数であるため、$\log_{c}a \neq 0$　となり、
$\log_{a}b = \frac{\log_{c}b }{\log_{c}a}$
が得られた。
証明終わり。 $\qquad \qquad \qquad \Box$

指数関数と対数関数の微分