経路問題
提供: Internet Web School
目次 |
有向グラフ
有向グラフは,ここではUNIQ6df46bf654174fe-MathJax-165-QINUで表すが,コンピュータや,ネットワークにもよく使われる。有向グラフUNIQ6df46bf654174fe-MathJax-166-QINUは
(1) 節点の集合UNIQ6df46bf654174fe-MathJax-167-QINU
(2) UNIQ6df46bf654174fe-MathJax-168-QINUの点の順序対UNIQ6df46bf654174fe-MathJax-169-QINUの集合UNIQ6df46bf654174fe-MathJax-170-QINU
からなる.
UNIQ6df46bf654174fe-MathJax-171-QINUのときUNIQ6df46bf654174fe-MathJax-172-QINUである.
また
UNIQ6df46bf654174fe-MathJax-173-QINU
UNIQ6df46bf654174fe-MathJax-174-QINUはUNIQ6df46bf654174fe-MathJax-175-QINUの自乗直積 UNIQ6df46bf654174fe-MathJax-176-QINU の部分集合である. すなわち,
UNIQ6df46bf654174fe-MathJax-177-QINU
順序対UNIQ6df46bf654174fe-MathJax-178-QINUは向きのついた枝,あるいは弧と呼ばれ,
(図5.1) 
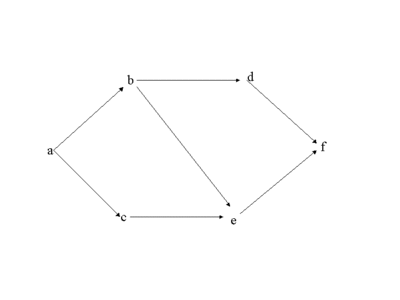
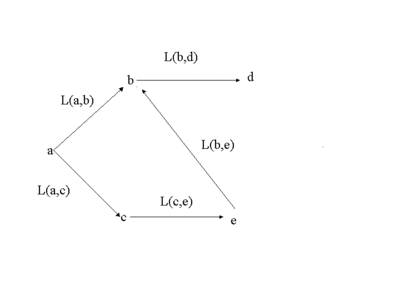
のように表すことができる。UNIQ6df46bf654174fe-MathJax-179-QINUは始点,UNIQ6df46bf654174fe-MathJax-180-QINUは終点と呼ばれる。 このような枝のまたは弧の図をつなぎ合わせば,有向グラフ UNIQ6df46bf654174fe-MathJax-181-QINUを平面図で表すことができる。
(図5.2) 
UNIQ6df46bf654174fe-MathJax-182-QINU
ラベル
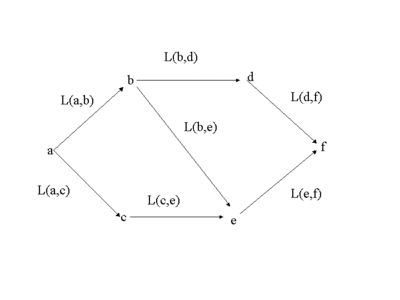
有向グラフUNIQ6df46bf654174fe-MathJax-183-QINUの弧には,長さや,所要時間などのデータでラベル付けされているとき UNIQ6df46bf654174fe-MathJax-184-QINUをラベル付き有向グラフといいます。
(図5.3) 
路
節点の多重対 UNIQ6df46bf654174fe-MathJax-185-QINUで,各UNIQ6df46bf654174fe-MathJax-186-QINUがUNIQ6df46bf654174fe-MathJax-187-QINU の元,すなわち弧であるものを 路といいます。
上の図では,UNIQ6df46bf654174fe-MathJax-188-QINUなどが路である.
最短路問題
UNIQ6df46bf654174fe-MathJax-189-QINUをラベル付き有向グラフとする。ただし,
(図5.4) 
のUNIQ6df46bf654174fe-MathJax-190-QINUのように「閉じた路」は含まないものとする。
さて,簡単にするため、集合UNIQ6df46bf654174fe-MathJax-191-QINUがUNIQ6df46bf654174fe-MathJax-192-QINU個の節点からなっているとして
UNIQ6df46bf654174fe-MathJax-193-QINUとし,夫々の弧に付けられている,ラベルはその弧の長さを 表すものとしておく。
(図5.5) 
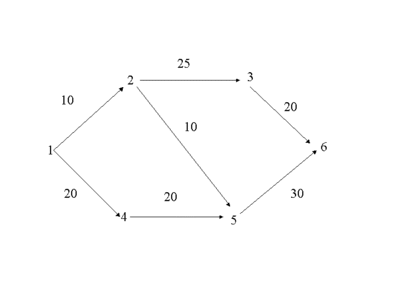
弧をつなぎ合わせて作られる路の長さは,それを構成している弧の長さの和で 表します。例えば(図5)で路UNIQ6df46bf654174fe-MathJax-194-QINUの長さは,UNIQ6df46bf654174fe-MathJax-195-QINUでUNIQ6df46bf654174fe-MathJax-196-QINUである.
節点1から出発して,節点nへ行くための長さ最小の路をどう求めるかという問題を考えます。(図5.5)の例では,路(1,2,5,6)が解で,長さUNIQ6df46bf654174fe-MathJax-197-QINUである.
UNIQ6df46bf654174fe-MathJax-198-QINUの点の数が少なければ,路を全て調べてみるのも一つの方法であるが,数が多くなると 実用的ではない。
D.P.(ダイナミック・プログラミング)と最短路
D.P.の原理
(図5.6) 
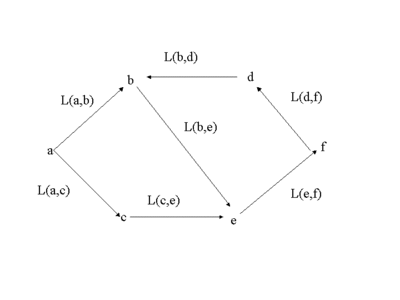
節点UNIQ6df46bf654174fe-MathJax-199-QINUから節点UNIQ6df46bf654174fe-MathJax-200-QINUへの最短路が与えられたとする。その路が途中に節点UNIQ6df46bf654174fe-MathJax-201-QINUを経由しているとすると, その経路のUNIQ6df46bf654174fe-MathJax-202-QINUからUNIQ6df46bf654174fe-MathJax-203-QINUへの部分の路も,やはりUNIQ6df46bf654174fe-MathJax-204-QINUからUNIQ6df46bf654174fe-MathJax-205-QINUへの最短経路になっている.
実際,UNIQ6df46bf654174fe-MathJax-206-QINUからUNIQ6df46bf654174fe-MathJax-207-QINUへの別の最短路があったとすると,例えば,(図6)の 節点UNIQ6df46bf654174fe-MathJax-208-QINUを経由して,UNIQ6df46bf654174fe-MathJax-209-QINUに行く路がそうであったとすると
UNIQ6df46bf654174fe-MathJax-210-QINU
となり,これから
UNIQ6df46bf654174fe-MathJax-211-QINU
であるから,路UNIQ6df46bf654174fe-MathJax-212-QINUが最短路UNIQ6df46bf654174fe-MathJax-213-QINUより短くなってしまい, 路UNIQ6df46bf654174fe-MathJax-214-QINUが最短であることに矛盾する.
結局, 「全体が最短（最適）ならその部分も最短（最適）」 である.
このような,性質を体系的に扱った最適化法の研究がベルマンによってなされた.
ベルマンのUNIQ6df46bf654174fe-MathJax-215-QINU（ダイナミック・プログラミング）とか最適性の原理と呼ばれている.
再帰的な計算法
最適性の原理を使うと,例えば,接点UNIQ6df46bf654174fe-MathJax-216-QINUからUNIQ6df46bf654174fe-MathJax-217-QINUまでの路が存在するとして,その中の 最短路UNIQ6df46bf654174fe-MathJax-218-QINUの長さをUNIQ6df46bf654174fe-MathJax-219-QINUで表すと
UNIQ6df46bf654174fe-MathJax-220-QINUからUNIQ6df46bf654174fe-MathJax-221-QINUまでの弧UNIQ6df46bf654174fe-MathJax-222-QINUが存在しない場合はUNIQ6df46bf654174fe-MathJax-223-QINU としておき,
UNIQ6df46bf654174fe-MathJax-224-QINU
UNIQ6df46bf654174fe-MathJax-225-QINU
という「再帰的」な定義ができる。
ここで,UNIQ6df46bf654174fe-MathJax-226-QINUとする。
これは,節点UNIQ6df46bf654174fe-MathJax-227-QINUからの弧UNIQ6df46bf654174fe-MathJax-228-QINUが存在する節点UNIQ6df46bf654174fe-MathJax-229-QINUについて,
節点UNIQ6df46bf654174fe-MathJax-230-QINUから節点UNIQ6df46bf654174fe-MathJax-231-QINU までの最短の長さUNIQ6df46bf654174fe-MathJax-232-QINUをもつ路UNIQ6df46bf654174fe-MathJax-233-QINUと 長さUNIQ6df46bf654174fe-MathJax-234-QINUの弧UNIQ6df46bf654174fe-MathJax-235-QINU をつなげた路UNIQ6df46bf654174fe-MathJax-236-QINU の長さ
UNIQ6df46bf654174fe-MathJax-237-QINU
のうち,最短のものがUNIQ6df46bf654174fe-MathJax-238-QINUであるという意味である.
(図5.5)
に適用すると
UNIQ6df46bf654174fe-MathJax-239-QINU
Dijkstraの方法
DPの原理を使った効率的な方法として,Dijkstraの方法が知られている. Dijkstraのアルゴリズム (Wikipedia)
準備 UNIQ6df46bf654174fe-MathJax-240-QINU
手順1 UNIQ6df46bf654174fe-MathJax-241-QINU
UNIQ6df46bf654174fe-MathJax-242-QINU
手順2 UNIQ6df46bf654174fe-MathJax-243-QINU
UNIQ6df46bf654174fe-MathJax-244-QINUがUNIQ6df46bf654174fe-MathJax-245-QINUの元で,かつ,UNIQ6df46bf654174fe-MathJax-246-QINUがUNIQ6df46bf654174fe-MathJax-247-QINU の要素となる全てのUNIQ6df46bf654174fe-MathJax-248-QINU に対して以下の手続き[]を繰り返す。
[もしUNIQ6df46bf654174fe-MathJax-249-QINU ならば UNIQ6df46bf654174fe-MathJax-250-QINU そうでなければ何もしない.]
手順1にもどる。
このアルゴリズムの終了時には,
UNIQ6df46bf654174fe-MathJax-251-QINUには節点UNIQ6df46bf654174fe-MathJax-252-QINUから節点UNIQ6df46bf654174fe-MathJax-253-QINUへの最短の長さ, UNIQ6df46bf654174fe-MathJax-254-QINUには節点UNIQ6df46bf654174fe-MathJax-255-QINUから節点UNIQ6df46bf654174fe-MathJax-256-QINUへの最短路で,節点UNIQ6df46bf654174fe-MathJax-257-QINUの直前の節点の番号
が書き込まれている.
以下このDijkstraの方法を図5の例に適用してみる.
図5.5は、
UNIQ6df46bf654174fe-MathJax-258-QINU
準備 UNIQ6df46bf654174fe-MathJax-259-QINU
UNIQ6df46bf654174fe-MathJax-260-QINU を999として
UNIQ6df46bf654174fe-MathJax-261-QINU
手順１(1回目) UNIQ6df46bf654174fe-MathJax-262-QINU
となり、m=1を選ぶ｡
手順２(1回目) UNIQ6df46bf654174fe-MathJax-263-QINU
手順１(2回目) UNIQ6df46bf654174fe-MathJax-264-QINU
となり、UNIQ6df46bf654174fe-MathJax-265-QINUを選ぶ｡
手順２(２回目) UNIQ6df46bf654174fe-MathJax-266-QINU
手順１(３回目) UNIQ6df46bf654174fe-MathJax-267-QINU
手順２(３回目) UNIQ6df46bf654174fe-MathJax-268-QINU
手順１(４回目) UNIQ6df46bf654174fe-MathJax-269-QINU
となり、UNIQ6df46bf654174fe-MathJax-270-QINUを選ぶ｡
手順２(４回目) UNIQ6df46bf654174fe-MathJax-271-QINU
手順１(５回目) UNIQ6df46bf654174fe-MathJax-272-QINU
となりUNIQ6df46bf654174fe-MathJax-273-QINUを選ぶ｡
手順２(５回目) UNIQ6df46bf654174fe-MathJax-274-QINU
手順１(６回目) UNIQ6df46bf654174fe-MathJax-275-QINU
となり、UNIQ6df46bf654174fe-MathJax-276-QINUを選ぶ｡
手順２(６回目) UNIQ6df46bf654174fe-MathJax-277-QINU
手順１(７回目) UNIQ6df46bf654174fe-MathJax-278-QINUなのでUNIQ6df46bf654174fe-MathJax-279-QINUとなり終了
節点1から節点UNIQ6df46bf654174fe-MathJax-280-QINUへの最短の長さ UNIQ6df46bf654174fe-MathJax-281-QINU 節点1から節点6への最短路で節点6の直前の節点の番号 UNIQ6df46bf654174fe-MathJax-282-QINU
無向グラフ
最短路問題ではラベル付き有向グラフを扱ったが,ここでは,弧で結ばれている節点間は, 双方向に行き来できるものとする。
従って,図示した場合も始点,終点といった「向き」はない。 このようなグラフUNIQ6df46bf654174fe-MathJax-283-QINUは無向グラフと呼ばれる。これは UNIQ6df46bf654174fe-MathJax-284-QINU
からなる。
UNIQ6df46bf654174fe-MathJax-285-QINUである.
この非順序対\{a,b\}も弧と呼ぶことにする。有向グラフのような始点,終点はない．
(図5.7)
のように表すことができる。有向グラフと同様に枝のまたは弧の図をつなぎ合わせば,
グラフUNIQ6df46bf654174fe-MathJax-286-QINUを平面図で表すことができる。
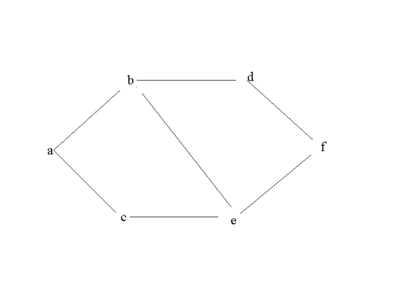
(図5.8)
UNIQ6df46bf654174fe-MathJax-287-QINU
ラベル
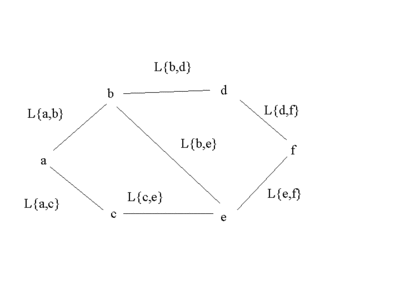
有向グラフと全く同様に無向グラフG=(P,V)の弧にも,長さや,所要時間などのデータでラベル付け することができる。
(図5.9)
路
有向グラフと同様に節点の多重対 UNIQ6df46bf654174fe-MathJax-288-QINUで,各UNIQ6df46bf654174fe-MathJax-289-QINU がUNIQ6df46bf654174fe-MathJax-290-QINUの元,すなわち弧であるものを 路と呼ぶことにする。
上の図では,UNIQ6df46bf654174fe-MathJax-291-QINUなどが路である.
巡回セールスマン問題
さて,簡単にするため,集合UNIQ6df46bf654174fe-MathJax-292-QINUがUNIQ6df46bf654174fe-MathJax-293-QINU個の節点からなっているとして
UNIQ6df46bf654174fe-MathJax-294-QINUとし,夫々の弧に付けられている,ラベルはその弧を移動する 費用は表すものとしておく。
(図5.10)
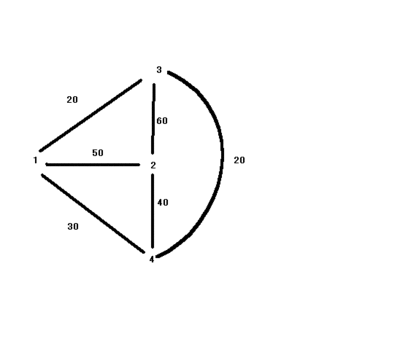
弧をつなぎ合わせて作られる路を移動する費用は,それを構成している弧の費用の和で 表します。上の図で路UNIQ6df46bf654174fe-MathJax-295-QINUの費用は,20+20+40で80である.
巡回セールスマン問題は,各節点を,例えば都市に,費用を運賃として,都市１を出発して各都市UNIQ6df46bf654174fe-MathJax-296-QINUを巡回（1回だけ訪れて）して, 再び都市１に戻ってくる,路の内費用最少の ものを求めるといった問題である.
(図5)の例では,路UNIQ6df46bf654174fe-MathJax-297-QINUとUNIQ6df46bf654174fe-MathJax-298-QINUが解で,費用が130である.
可能な路を全てを調べても,１番目の都市3通りUNIQ6df46bf654174fe-MathJax-299-QINU2番目の都市2通りUNIQ6df46bf654174fe-MathJax-300-QINU３番目の都市1通り=3!通りで順序を 逆に回っても同じであるから2で割って,結局3!/2通りである.しかし,都市の数が増えると非常に難しくなる。
D.P.の適用
有グラフ最短路問題と同様に最適性の原理を使って組織的に調べることができる。
例えば,都市UNIQ6df46bf654174fe-MathJax-301-QINUを出発して,UNIQ6df46bf654174fe-MathJax-302-QINUを巡回して,
最後に都市UNIQ6df46bf654174fe-MathJax-303-QINUを訪れるまでの最小費用をUNIQ6df46bf654174fe-MathJax-304-QINUで表すと, その最小になる路を通ってさらに都市UNIQ6df46bf654174fe-MathJax-305-QINUに戻ってくるまでの費用は
UNIQ6df46bf654174fe-MathJax-306-QINU
である.全く同様に,費用最少で,UNIQ6df46bf654174fe-MathJax-307-QINUを巡回後,都市3を訪れ,都市UNIQ6df46bf654174fe-MathJax-308-QINU に戻る費用は
UNIQ6df46bf654174fe-MathJax-309-QINU
UNIQ6df46bf654174fe-MathJax-310-QINUを巡回して,最後に都市4を訪れ,都市1に戻る費用は
UNIQ6df46bf654174fe-MathJax-311-QINU
である. 結局,最小の費用は
UNIQ6df46bf654174fe-MathJax-312-QINU
であり,その最少費用を実現する路が求めるものである.
有グラフの場合と同様にUNIQ6df46bf654174fe-MathJax-313-QINUも再帰的に, 都市1を出発して,UNIQ6df46bf654174fe-MathJax-314-QINUを巡回して,最後に都市2を訪れるまでの 最小費用であるから
都市1を出発して,UNIQ6df46bf654174fe-MathJax-315-QINUを巡回して都市3を訪れ,ついで都市2を訪れる費用
UNIQ6df46bf654174fe-MathJax-316-QINU
都市1を出発して,UNIQ6df46bf654174fe-MathJax-317-QINUを巡回して都市4を訪れ,ついで都市2を訪れる費用
UNIQ6df46bf654174fe-MathJax-318-QINU
のうち何れか小さい方：
UNIQ6df46bf654174fe-MathJax-319-QINU
で求められる。
さらに,
UNIQ6df46bf654174fe-MathJax-320-QINUは路UNIQ6df46bf654174fe-MathJax-321-QINUの費用であるからUNIQ6df46bf654174fe-MathJax-322-QINU
UNIQ6df46bf654174fe-MathJax-323-QINUは路UNIQ6df46bf654174fe-MathJax-324-QINUの費用であるからUNIQ6df46bf654174fe-MathJax-325-QINU
である.
結局,最小の費用は以下の再帰的な計算により求めることができる。
UNIQ6df46bf654174fe-MathJax-326-QINU
しかしながら,この方法は組織的ではあるが,「全件探索」(全ての可能な候補を全て当たる) であり,都市の数が１0～20ぐらいまでが限界である.
分岐限定法
ここで扱っている,巡回セールスマン問題には,解法の「決定打」はない。 問題の難しさを表す場合によく出てくる「NP困難問題」の一つである. 種々な方法が考案されている。「分岐限定法」もその一つである.
