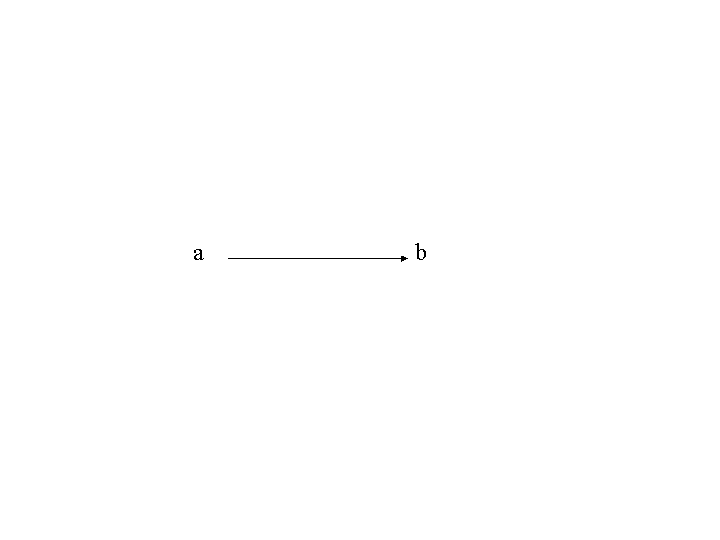経路問題
提供: Internet Web School
=={最短経路問題}
目次 |
ラベル付き有向グラフ
有向グラフ
有向グラフは,ここでは\(G\)で表しますが,コンピュータや,ネットワークにもよく使われ ます。有向グラフ\(G\)は
(1) 節点の集合\(P\)
(2) \(P\)の点の順序対\((a,b)(a,bはPの点)\)の集合\(V\)
からなる.
\(a \ne b\)のとき\((a,b) \ne (b,a)\)である.
また
\((a,b)=(c,d)\Leftrightarrow (a=c\ and\ b=d)\)
\(V\)は\(P\)の自乗直積 \(P \times P= \{(a,b)|a,bはPの要素 \} \) の部分集合である. すなわち,
\(V \subseteq P \times P\)
順序対\((a,b)\)は向きのついた枝,あるいは弧と呼ばれ,
のように表すことができる。\(a\)は始点,\(b\)は終点と呼ばれる。 このような枝のまたは弧の図をつなぎ合わせば,有向グラフ \(G=(P,V)\)を平面図で表すことができる。
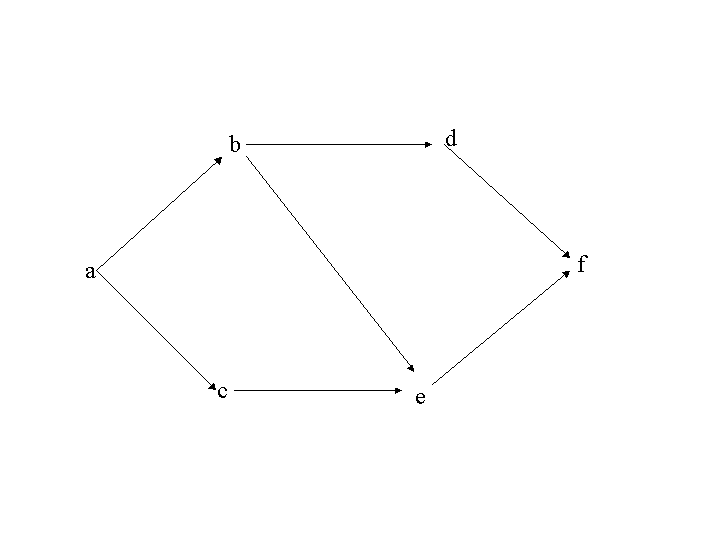
\(
P=\{ a,b,c,d,e,f \} \\
V=\{(a,b),(a,c),(b,d),(b,e),(c,e),(d,f),(e,f) \}
\)
ラベル
有向グラフ\(G=(P,V)\)の弧には,長さや,所要時間などのデータでラベル付けされているとき \(G\)をラベル付き有向グラフといいます。
路
節点の多重対 \((p_1,p_2,\cdots,p_k)\)で,各\((p_1,p_2),(p_2,p_3),\cdots,(p_{k-1},p_k)\)が\(V\) の元,すなわち弧であるものを 路といいます。
上の図では,\((a,b,e,f),(a,c,e),(b,d,f)\)などが路である.
最短路問題
\(G\)をラベル付き有向グラフとする。ただし,
の\((b,e,f,d,b)\)のように「閉じた路」は含まないものとする。
さて,簡単にするため、集合\(P\)が\(n\)個の節点からなっているとして
\(P=\{1,2,\cdots,n\}\)とし,夫々の弧に付けられている,ラベルはその弧の長さを 表すものとしておく。
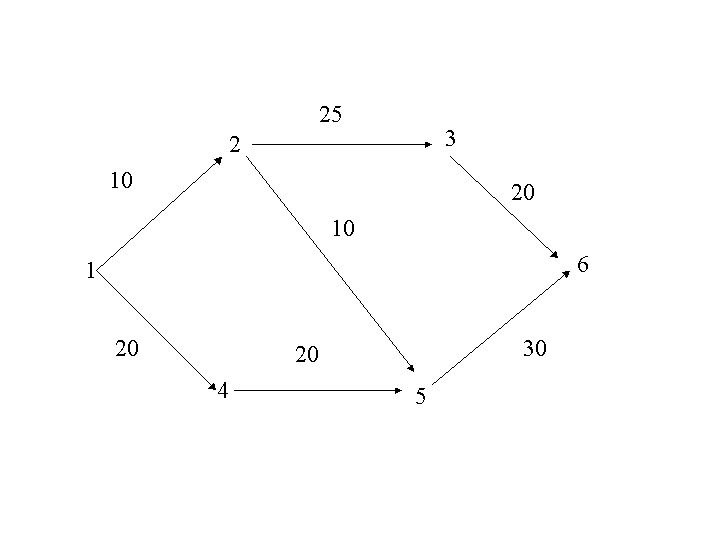
弧をつなぎ合わせて作られる路の長さは,それを構成している弧の長さの和で 表します。例えば(図5)で路\((1,4,5,6)\)の長さは,\(20+20+30\)で\(70\)である.
節点1から出発して,節点nへ行くための長さ最小の路をどう求めるかという問題を考えます。(図5.5)の例では,路(1,2,5,6)が解で,長さ\(50\)である.
\(P\)の点の数が少なければ,路を全て調べてみるのも一つの方法であるが,数が多くなると 実用的ではない。
D.P.(ダイナミック・プログラミング)と最短路
D.P.の原理
\vspace{5cm} \par
(図5.6)
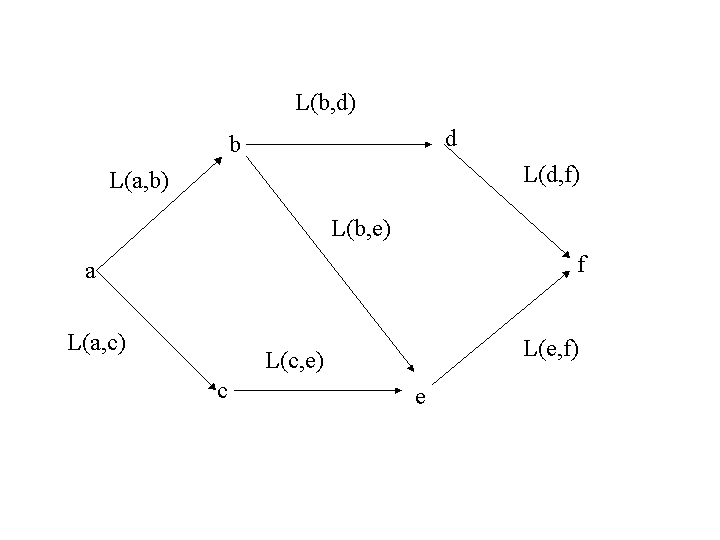
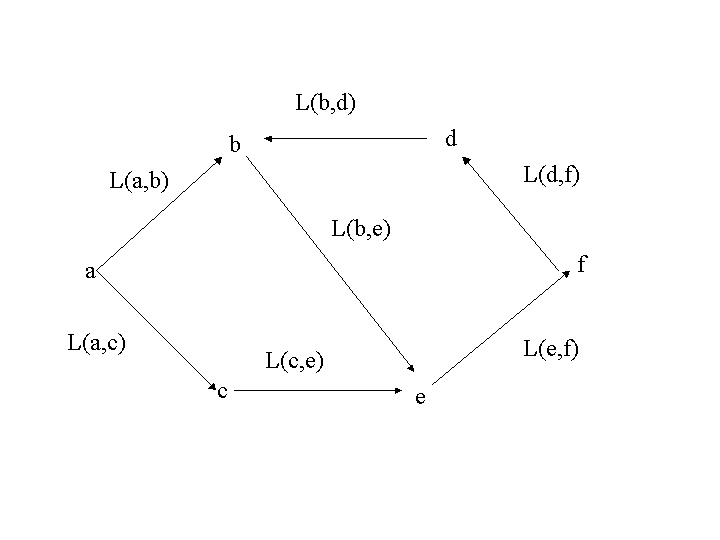
節点\(a\)から節点\(d\)への最短路が与えられたとする。その路が途中に節点bを経由しているとすると, その経路の\(a\)から\(b\)への部分の路も,やはり\(a\)から\(b\)への最短経路になっています。
実際,\(a\)から\(b\)への別の最短路があったとすると,例えば,(図6)の 節点\(c,e<math>を経由して,<math>b\)に行く路がそうであったとすると \( L(a,c)+L(c,e)+L(e,b) < L(a,b) \) となり,これから \( L(a,c)+L(c,e)+L(e,b)+L(b,d) < L(a,b)+ L(b,d) \) であるから,路\((a,c,e,b,d)\)が最短路\((a,b,d)\)より短くなってしまい, 路\((a,b,d)\)が最短であることに矛盾します。
結局, 「全体が最短(最適)ならその部分も最短(最適)」 ということになります。
このような,性質を体系的に扱った最適化法の研究がベルマンによってなされました。 ベルマンの\(D.P.\)(ダイナミック・プログラミング)とか最適性の原理と呼ばれています。
\item{再帰的な計算法}
最適性の原理を使うと,例えば,接点iからkまでの路が存在するとして,その中の 最短路\(R(i,k)\)の長さを\(O(i,k)\)で表すと
\(i<math>から<math>k\)までの弧\((i,k)\)が存在しない場合は\(L(i,k)=\infty\) としておき,
\( O(i,k)=min\{\{ L(i,k) \} \cup \{L(i,j)+O(j,k) |j \ne i,k,(i,j)はVの元\} \} (1a) R(i,k)=(i,k) (O(i,k)=L(i,k)のとき)=(i,R(j_0,k)) (上記以外でO(i,k)=L(i,j_0)+O(j_0,k),j_0 \ne i,k,(i,j0)はVの元となる j_0を一つ選択)(1b) \)
という「再帰的」な定義ができる。 ここで,\((i,(j,\cdots,k))=(i,j,\cdots,k)\)とする。 これは,節点iからの弧\((i,j)\)が存在する節点\(j\)について,節点\(j\)から節点\(k\) までの最短の長さ\(O(j,k)\)をもつ路\((j,\cdots,k)\)と長さ\(L(i,j)\)の弧\((i,j)\) をつなげた路\((i,j,\cdots,k)\) の長さ \(L(i,j)+O(j,k)\) のうち,最短のものが\(O(i,k)\)であるという意味である. \vspace{5cm}
(図5.5)
に適用すると
\(
O(3,6)=20 R(3,6)=(3,6)
O(5,6)=30 R(5,6)=(5,6)
O(2,6)
=min\{L(2,3)+O(3,6),L(2,5)+O(5,6)\}
=min\{25+20,10+30\} =40
R(2,6)=(2,5,6)
O(4,6)
=L(4,5)+O(5,6)
=50
R(4,6)=(4,R(5,6))=(4,5,6)
O(1,6)
=min\{L(1,2)+O(2,6),L(1,4)+O(4,6)\}
=min\{10+40,20+50\}
=50
R(1,6)=(1,R(2,6))=(1,2,5,6)
\)
Dijkstraの方法
DPの原理を使った効率的な方法として,Dijkstraの方法が知られています。 <Dijkstra>
準備
\( K \leftarrow \phi L \leftarrow P O(1) \leftarrow 0 j \ne 1となるPの要素j全てに対してO(j) \leftarrow \infty \)
手順1
\( K=Pなら終了 K \ne Pのとき O(m)=\min \{O(i)|iはLの元 \}となるLの元mを選ぶ。 \)
手順2
\( K \leftarrow K \cup \{m \}(Kに要素mを加えた集合を新たにKとする。) L \leftarrow L \setminus \{m \}(Lからその要素mを除いた集合を新たにLとする。) (m,j)がVの元で,かつ,jがLの要素となる全てのjに対して以下の<<>>内の手続きを繰り返す。 ~~<<もし,O(j) > O(m) + L(m,j) ならば ~~O(j) \leftarrow O(m) + L(m,j) ~~R(j) \leftarrow m ~~そうでなければ何もしない。>> \)
手順1にもどる。
このアルゴリズムの終了時には,
\(O(j)\)には節点\(1\)から節点\(j\)への最短の長さ, \(R(j)\)には節点\(1\)から節点\(j\)への最短路で,節点\(j\)の直前の節点の番号
が書き込まれています。
以下このDijkstraの方法を図5の例に適用してみます。 これは、本大学院の社会人学生「たなかさん」にやっていただいたものである. 図5.5は、
\( P=\{1,2,3,4,5,6\} V=\{(1,2),(1,4),(2,3),(2,5),(3,6),(4,5),(5,6)\} L(1,2)=10, L(1,4)=20, L(2,3)=25, L(2,5)=10, L(3,6)=20, L(4,5)=20, L(5,6)=30 \)
準備
\( K \leftarrow \phi L \leftarrow \{1,2,3,4,5,6\} O(1) \leftarrow 0 \infty を999として O(2) \leftarrow 999, O(3) \leftarrow 999, O(4) \leftarrow 999, O(5) \leftarrow 999, O(6) \leftarrow 999 \)
手順1(1回目)
\( K \ne Pなので終了ではない O(m)=min\{O(1),O(2),O(3),O(4),O(5),O(6)\} =O(1) =0 \)
となり、m=1を選ぶ。
\item{手順2(1回目)} \( K \leftarrow \{ 1\} L \leftarrow \{2,3,4,5,6\} << ~~j=2のとき ~~O(2)=999 ~~O(1) + L(1,2)=0+10=10なので ~~O(2) > O(1) + L(1,2) となり ~~O(2) \leftarrow 10 ~~R(2) \leftarrow 1 ~~j=3のとき ~~(1,3)はVの元ではない。 ~~j=4のとき ~~O(4) = 999 ~~O(1) + L(1,4) = 0 + 20 = 20 ~~O(4) > O(1) + L(1,4)となり ~~O(4) \leftarrow 20 ~~R(4) \leftarrow 1 ~~j=5,6のとき ~~(1,5),(1,6)はVの元ではない ~>> \)
手順1(2回目)
\( K=\{1 \}なのでK \ne Pとなり終了ではない O(2)=10, O(3)=999, O(4)=20, O(5)=999, O(6)=999なので O(m)=min\{O(2),O(3),O(4),O(5),O(6)\} =O(2) =10 \)
となり、\(m=2\)を選ぶ。
手順2(2回目)
\( K \leftarrow \{1\} \cup \{2\}=\{1,2\} L \leftarrow \{3,4,5,6\} << ~~j=3のとき ~~O(3)=999 ~~O(2) + L(2,3)=10+25=35なので ~~O(3) > O(2) + L(2,3) となり ~~O(3) \leftarrow 35 ~~R(3) \leftarrow 2 ~~j=4のとき ~~(2,4)はVの元ではない。 ~~j=5のとき ~~O(5) = 999 ~~O(2) + L(2,5) = 10 + 10 = 20 ~~O(5) > O(2) + L(2,5)となり ~~O(5) \leftarrow 20 ~~R(5) \leftarrow 2 ~~j=6 ~~(2,6)はVの元ではない ~>> \)
手順1(3回目)
\( K=\{1,2\}なのでK \ne Pとなり終了ではない O(3)=35,O(4)=20,O(5)=20,O(6)=999なので O(m)=min\{O(3),O(4),O(5),O(6)\} =O(4) =20 となり、m=4を選ぶ。 \)
手順2(3回目)
\( K \leftarrow \{1,2,4\} L \leftarrow \{3,5,6\} << ~j=3のとき ~(4,3)はVの元ではない ~j=5のとき ~O(5)=20 ~O(4) + L(4,5) = 20 + 20 = 40 ~O(5) < O(4) + L(4,5)となり、何もしない ~j=6 ~(4,6)はVの元ではない ~>> \)
手順1(4回目)
\( K=\{1,2,4\}なのでK \ne Pとなり終了ではない O(3)=35,O(5)=20,O(6)=999なので O(m)=min\{O(3),O(5),O(6)\} =O(5) =20 \)
となり、\(m=5\)を選ぶ。
手順2(4回目)
\( K \leftarrow \{1,2,4,5\} L \leftarrow \{3,6\} [[利用者:Moderator|Moderator]]<< ~~j=3のとき ~~(5,3)はVの元ではない ~~j=6のとき ~~O(6)=999 ~~O(5) + L(5,6) = 20 + 30 = 50 O(6) > O(5) + L(5,6)となり ~~O(6) \leftarrow 50 ~~R(6) \leftarrow 5 ~>> \)
手順1(5回目)
\( K=\{1,2,4,5\}なのでK \ne Pとなり終了ではない O(3)=35,O(6)=50なので O(m)=min\{O(3),O(6)\} =O(3) =35 \) となり、\(m=3\)を選ぶ。
手順2(5回目)
\( K \leftarrow \{1,2,3,4,5\} L \leftarrow \{6\} ~~<< ~j=6のとき ~O(6)=50 ~O(3) + L(3,6) = 35 + 20 = 55 ~O(6) < O(3) + L(3,6)となり何もしない >> \)
手順1(6回目)
\( K=\{1,2,3,4,5\}なのでK \ne Pとなり終了ではない O(6)=50なので O(m)=min\{O(6)\} =O(6) =50 \)
となり、\(m=6\)を選ぶ。
手順2(6回目)
\( K \leftarrow \{1,2,3,4,5,6\} L \leftarrow \phi << Lの要素がない >> \)
手順1(7回目)
\(K=\{1,2,3,4,5,6\}\)なので\(K=P\)となり終了
節点1から節点\(6\)への最短の長さ \(O(6)=50\) 節点1から節点6への最短路で節点6の直前の節点の番号 \(R(6)=5\)
無向グラフ
最短路問題ではラベル付き有向グラフを扱ったが,ここでは,弧で結ばれている節点間は, 双方向に行き来できるものとする。従って,図示した場合も始点,終点といった「向き」はない。 このようなグラフ\(G\)は無向グラフと呼ばれる。これは \( (1)節点の集合P (2)Pの点の非順序対\{a,b\}( a,bはPの点)の集合V \)
からなります。
\(\{a,b\}=\{b,a\}\)である.
この非順序対\{a,b\}も弧と呼ぶことにする。有向グラフのような始点,終点はない.
\vspace{2cm} \par
(図5.7)
のように表すことができる。有向グラフと同様に枝のまたは弧の図をつなぎ合わせば, グラフ\(G=(P,V)\)を平面図で表すことができる。
\vspace{5cm} \par
(図5.8) \( P=\{a,b,c,d,e,f\} V=\{\{a,b\},\{a,c\},\{b,d\},\{b,e\},\{c,e\},\{d,f\},\{e,f\}\} \)
ラベル
有向グラフと全く同様に無向グラフG=(P,V)の弧にも,長さや,所要時間などのデータでラベル付け することができる。
\vspace{5cm} \par
(図5.9)
路
有向グラフと同様に節点の多重対 \((p_1,p_2,\cdots,p_k)\)で,各\(\{p_1,p_2\},\{p_2,p_3\},\cdots,\{p_{k-1},p_k\}\) が\(V\)の元,すなわち弧であるものを 路と呼ぶことにする。
上の図では,\((a,b,e,f),(a,c,e),(b,d,f)\)などが路である.
巡回セールスマン問題
さて,簡単にするため,集合\(P\)が\(n\)個の節点からなっているとして
\(P=\{1,2,\cdots,n\}\)とし,夫々の弧に付けられている,ラベルはその弧を移動する 費用は表すものとしておく。 下の図では,節点の番号と区別できるよう()付の数字で表しておく。
\vspace{5cm} \par
(図5.10)
弧をつなぎ合わせて作られる路を移動する費用は,それを構成している弧の費用の和で 表します。上の図で路\((1,3,4,2)\)の費用は,20+20+40で80である.
巡回セールスマン問題は,各節点を,例えば都市に,費用を運賃として,都市1を出発して各都市\((2,3,4)\)を巡回(1回だけ訪れて)して, 再び都市1に戻ってくる,路の内費用最少の ものを求めるといった問題である.
(図5)の例では,路\((1,3,4,2,1)\)と\((1,2,4,3,1)\)が解で,費用が130である. 可能な路を全てを調べても,1番目の都市3通り\(\times\)2番目の都市2通り\(\times\)3番目の都市1通り=3!通りで順序を 逆に回っても同じであるから2で割って,結局3!/2通りである.しかし,都市の数が増えると非常に難しくなります。
D.P.の適用
有グラフ最短路問題と同様に最適性の原理を使って組織的に調べることができる。
例えば,都市\(1\)を出発して,\(\{2,3,4\}\)を巡回して, 最後に都市\(2\)を訪れるまでの最小費用を\(Cost(\{2,3,4\},2)\)で表すと, その最小になる路を通ってさらに都市\(1\)に戻ってくるまでの費用は \(Cost(\{2,3,4\},2)+L\{2,1\}\) である.全く同様に,費用最少で,\(\{2,3,4\}\)を巡回後,都市3を訪れ,都市\(1\) に戻る費用は \(Cost(\{2,3,4\},3)+L\{3,1\}\) \(\{2,3,4\}\)を巡回して,最後に都市4を訪れ,都市1に戻る費用は \(Cost(\{2,3,4\},4)+L\{4,1\}\) である. 結局,最小の費用は \(min\{Cost(\{2,3,4\},2)+L\{2,1\},Cost(\{2,3,4\},3)+L\{3,1\} , Cost(\{2,3,4\},4)+L\{4,1\}\}\) であり,その最少費用を実現する路が求めるものである.
有グラフの場合と同様に\(Cost(\{2,3,4\},2)\)も再帰的に, 都市1を出発して,\(\{3,4\}\)を巡回して,最後に都市2を訪れるまでの 最小費用であるから 都市1を出発して,\(\{3,4\}\)を巡回して都市3を訪れ,ついで都市2を訪れる費用 \(Cost(\{3,4\},3)+L\{3,2\}\) 都市1を出発して,\(\{3,4\}\)を巡回して都市4を訪れ,ついで都市2を訪れる費用 \(Cost(\{3,4\},4)+L\{4,2\}\) のうち何れか小さい方: \(min\{Cost(\{3,4\},3)+L\{3,2\},Cost(\{3,4\},4)+L\{4,2\}\}\) で求められる。 さらに, \(Cost(\{3,4\},3)\)は路\((1,4,3)\)の費用であるから\(L\{1,4\}+L\{4,3\}=30+20=50\) \(Cost(\{3,4\},4)\)は路\((1,3,4)\)の費用であるから\(L\{1,3\}+L\{3,4\}=20+20=40\) である.
結局,最小の費用は以下の再帰的な計算により求めることができる。 \( min\{Cost(\{2,3,4\},2)+L\{2,1\},Cost(\{2,3,4\},3)+L\{3,1\} ,Cost(\{2,3,4\},4)+L\{4,1\} \} =min\{ 80+50,110+20 ,120+30 \} =130 (1,3,4,2,1)または (1,2,4,3,1) Cost(\{2,3,4\},2) =min\{Cost(\{3,4\},3)+L\{3,2\},Cost(\{3,4\},4)+L\{4,2\}\} =min\{50+60,40+40\}=80 路は(1,3,4,2) Cost(\{3,4\},3)=L\{1,4\}+L\{4,3\}=30+20=50 Cost(\{3,4\},4)=L\{1,3\}+L\{3,4\}=20+20=40 Cost(\{2,3,4\},3) =min\{Cost(\{2,4\},2)+L\{2,3\},Cost(\{2,4\},4)+L\{4,3\}\} =min\{70+60,90+20\}=110 路は(1,2,4,3) Cost(\{2,4\},2)=L\{1,4\}+L\{4,2\}=30+40=70 Cost(\{2,4\},4)=L\{1,2\}+L\{2,4\}=50+40=90 Cost(\{2,3,4\},4) =min\{Cost(\{2,3\},2)+L\{2,4\},Cost(\{2,3\},3)+L\{3,4\}\} =min\{80+40,110+20\}=120 路は (1,3,2,4) Cost(\{2,3\},2)=L\{1,3\}+L\{3,2\}=20+60=80 Cost(\{2,3\},3)=L\{1,2\}+L\{2,3\}=50+60=110 \)
しかしながら,この方法は組織的ではありますが,「全件探索」(全ての可能な候補を全て当たる) であり,都市の数が10~20ぐらいまでが限界である.
分岐限定法
ここで扱っている,巡回セールスマン問題には,解法の「決定打」はない。 問題の難しさを表す場合によく出てくる「NP困難問題」の一つである. 種々な方法が考案されている。「分岐限定法」もその一つである.
かなり作為的であるが,以下の例を考えます。 \vspace{5cm} \par
(図5.11)
都市1を出発し,各都市を1回ずつ訪れ,都市1に戻ってくる路を全て,逆周りも含めて,列挙すれば, \( (1,2,3,4,1), (1,2,4,3,1), (1,3,2,4,1), (1,3,4,2,1), (1,4,2,3,1), (1,4,3,2,1) \)
である.これらの路は1番目,2番目,3番目に訪れる都市によって分類できる。 例えば,1番目に訪れる都市に注目して
(?)1番目の都市が2のもの \((1,2,3,4,1),(1,2,4,3,1)\)>
(?)1番目の都市が3のもの \((1,3,2,4,1),(1,3,4,2,1)\)>
(?)1番目の都市が4のもの \( (1,4,2,3,1),(1,4,3,2,1)\)>
である.?,?,?の中でそれぞれ,最少費用の路を探す問題は部分問題と呼ばれる。 さらに?,?,?の分類を2番目,3番目によって,細かく分類ができる。解の候補の「分岐」がでてくるわけである.
ここで,解の候補として路の\((1,3,4,2,1)\)を選んだとする。この路の費用は130である. 部分問題?,すなわち,?の分類の中で費用最少を調べ見ると: 路(弧)</math>(1,4)</math>だけで,既に費用が130であり,費用がマイナスの弧はないのであるから, この?の分類のものの最少費用は130より大である.従って,これ以上細かく調べる必要はない。 すると,解は,路の\((1,3,4,2,1)\)を含む,(?)か(?)から探せばよい事になります。 このようにして,探すべき解の候補の「枝」のうち,無駄なものを削除する事ができる。
さらに,路\((1,2,3),(1,3,2)\)も費用が130であるから,これらの後の節点がなんであろうと,費用は 130より大きくなります。この例では,以後の分岐はないので,これが判っても効用はあり ませんが,もしさらに分岐があるなら,無駄な「枝」を削除できることになります。
この様にして,結局, \( (1,3,4,2,1), (1,2,4,3,1) \) にたどりつく。
無論,問題のよって,また,部分問題にの作製(分類)の仕方によって,最悪,全ての路を調べる事に なる場合もあります。以上のような解法を一般的に表すと,
最小化問題\(P\)が与えられたとして:
===(1)=== \(P\)から,部分問題の集合\(L=\{P_0,P_1,P_2,\cdots,P_n\}\)を作り,
初期解を適当に選択してその値\(C_0\)を求める。
以下の手続きを\(L\)の元\(P_i\)の全てについて行う
===(2)===最小問題\(P_i\)の解の下限値\(inf P_i\)を求め,
\(inf P_i > C_0\)なら \(L \leftarrow L \setminus \{P_i\}\)
\((LからP_iを削除)\)
===(3)=== 最小問題\(P_i\)の解\(min P_i<m/ath>を求め <math>min P_i < C_0\)なら \(C_0 \leftarrow min P_i\) とする
図5.10の問題について,「分岐限定法」を適用すると例えば以下のようになります。
これは、本大学院の社会人学生久保さんにやっていただいたものである.上の例より
スマートな解法である.
都市1を出発し,各都市を1回ずつ訪れ,都市1に戻ってくる路を全て,逆周りも含めて,列挙すると,
\((1,2,3,4,1),(1,2,4,3,1),(1,3,2,4,1),(1,3,4,2,1),(1,4,2,3,1),(1,4,3,2,1)\)>
である.これらの路は費用最小の\(\{1,3\},\{3,4\}\)の両方を通るものと, 通らないものに分類できる.
\(\{1,3\},\{3,4\}\)の両方を通るもの
\((1,2,4,3,1),(1,3,4,2,1)\)>
\item{(?)}\{1,3\},\{3,4\}の両方は通らないもの
\((1,2,3,4,1),(1,3,2,4,1),(1,4,2,3,1),(1,4,3,2,1)\)>
である.
ここで,解の候補として(?)から路\((1,2,4,3,1)\)を選んだとする. この路の費用は130である.
部分問題(?)で費用を調べて見ると,費用20の路が1つしか通れないことから, 各路の費用は \(20,30,40,50,60\) で,この中から4つを選ぶことから下限値は140となる. 140>130なので,は削除できる.
残った()から探せばよい事になるが,路(1,3,4,2,1)の費用も130となり, \((1,3,4,2,1),(1,2,4,3,1)\)> にたどりつく.
図5.11の問題について,「D.P.」を適用すると:
\(
min\{Cost(\{2,3,4\},2)+L\{2,1\},Cost(\{2,3,4\},3)+L\{3,1\}
,Cost(\{2,3,4\},4)+L\{4,1\} \}
=min\{ 80+50,110+20 ,140+130 \}
=130 (1,3,4,2,1)または (1,2,4,3,1)
Cost(\{2,3,4\},2)
=min\{Cost(\{3,4\},3)+L\{3,2\},Cost(\{3,4\},4)+L\{4,2\}\}
=min\{150+80,40+40\}=80 路は(1,3,4,2)
Cost(\{3,4\},3)=L\{1,4\}+L\{4,3\}=130+20=150
Cost(\{3,4\},4)=L\{1,3\}+L\{3,4\}=20+20=40
Cost(\{2,3,4\},3)
=min\{Cost(\{2,4\},2)+L\{2,3\},Cost(\{2,4\},4)+L\{4,3\}\}
=min\{170+80,90+20\}=110 路は(1,2,4,3)
Cost(\{2,4\},2)=L\{1,4\}+L\{4,2\}=130+40=170
Cost(\{2,4\},4)=L\{1,2\}+L\{2,4\}=50+40=90
Cost(\{2,3,4\},4)
=min\{Cost(\{2,3\},2)+L\{2,4\},Cost(\{2,3\},3)+L\{3,4\}\}
=min\{100+40,130+20\}=140 路は (1,3,2,4)
Cost(\{2,3\},2)=L\{1,3\}+L\{3,2\}=20+80=100
Cost(\{2,3\},3)=L\{1,2\}+L\{2,3\}=50+80=130
\)