線形計画法
提供: Internet Web School
メディア:Example.ogg線形計画法は 線形計画法 (Wikipedia)に説明がある.
解法には
シンプレックス法(Wikipedia)や内点法(Wikipedia)がある. シンプレクス法は[菅沼]の解説が判りやすい.
ここでは2つの例を用いて説明する. Microsoft Excel のソルバーを用いた解法例も説明する.
生産計画
例題1
ある製造会社があって, UNIQ2cca723c10bf8fe1-MathJax-77-QINU と UNIQ2cca723c10bf8fe1-MathJax-78-QINU という2種類の製品の製造販売をしている. これらを製造するには, 原材料UNIQ2cca723c10bf8fe1-MathJax-79-QINU,UNIQ2cca723c10bf8fe1-MathJax-80-QINU,UNIQ2cca723c10bf8fe1-MathJax-81-QINUが必要で, UNIQ2cca723c10bf8fe1-MathJax-82-QINU, UNIQ2cca723c10bf8fe1-MathJax-83-QINUをそれぞれ1単位当 たり造るのに必要な量と, 使用できる在庫量が下の表のように決まっている.
| 原材料\製品 | x | y | 在庫量 |
| A | 10 | 20 | 400 |
| B | 20 | 10 | 600 |
| C | 15 | 40 | 1300 |
UNIQ2cca723c10bf8fe1-MathJax-84-QINU, UNIQ2cca723c10bf8fe1-MathJax-85-QINUを販売するとそれぞれ1単位当たり2万円, 1万円の利益が得られる. 問題は, 表の在庫量の範囲で, UNIQ2cca723c10bf8fe1-MathJax-86-QINUとUNIQ2cca723c10bf8fe1-MathJax-87-QINUをそれぞれ何単位ずつ造れば利益が最大に なるかである。
線形計画法(1)
これを数式化すると, UNIQ2cca723c10bf8fe1-MathJax-88-QINU, UNIQ2cca723c10bf8fe1-MathJax-89-QINUの製造量をUNIQ2cca723c10bf8fe1-MathJax-90-QINU, UNIQ2cca723c10bf8fe1-MathJax-91-QINUで表すとして:
原材料UNIQ2cca723c10bf8fe1-MathJax-92-QINU, UNIQ2cca723c10bf8fe1-MathJax-93-QINU, UNIQ2cca723c10bf8fe1-MathJax-94-QINUについての制約から
UNIQ2cca723c10bf8fe1-MathJax-95-QINU
負の生産量はないのであるから
UNIQ2cca723c10bf8fe1-MathJax-96-QINU
利益は
UNIQ2cca723c10bf8fe1-MathJax-97-QINU
で結局, (6)をUNIQ2cca723c10bf8fe1-MathJax-98-QINUの条件のもとで最大にすることになる。
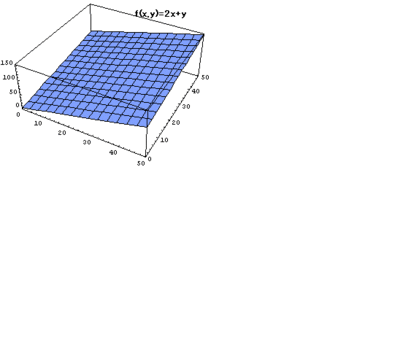
下の図は関数UNIQ2cca723c10bf8fe1-MathJax-99-QINUの図である。
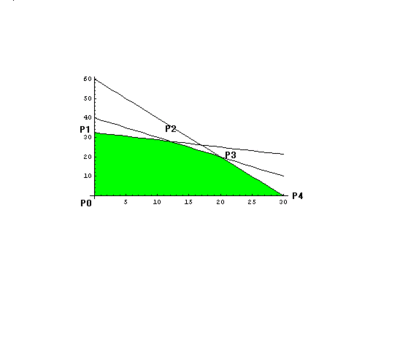
条件UNIQ2cca723c10bf8fe1-MathJax-100-QINUを充たす点UNIQ2cca723c10bf8fe1-MathJax-101-QINUは 下のような,凸多角形の境界線も含めた内部にある。
この凸多角形の頂点を UNIQ2cca723c10bf8fe1-MathJax-102-QINU とすると,
内部の点UNIQ2cca723c10bf8fe1-MathJax-103-QINUはこれらの頂点UNIQ2cca723c10bf8fe1-MathJax-104-QINUによって
UNIQ2cca723c10bf8fe1-MathJax-105-QINU
で表される。これをUNIQ2cca723c10bf8fe1-MathJax-106-QINUの凸結合という.
UNIQ2cca723c10bf8fe1-MathJax-107-QINU
には「線形性」が成り立っている.
これは UNIQ2cca723c10bf8fe1-MathJax-108-QINU
とUNIQ2cca723c10bf8fe1-MathJax-109-QINUについて,
UNIQ2cca723c10bf8fe1-MathJax-110-QINU
という性質である。この線形性を使うと,以下の議論ができる。
まず各頂点での関数UNIQ2cca723c10bf8fe1-MathJax-111-QINUの値
UNIQ2cca723c10bf8fe1-MathJax-112-QINU
のうち最大値をUNIQ2cca723c10bf8fe1-MathJax-113-QINUとする.
凸多角形の内の任意の点UNIQ2cca723c10bf8fe1-MathJax-114-QINUに対するUNIQ2cca723c10bf8fe1-MathJax-115-QINUは
UNIQ2cca723c10bf8fe1-MathJax-116-QINUがUNIQ2cca723c10bf8fe1-MathJax-117-QINU の凸結合で表されることから
UNIQ2cca723c10bf8fe1-MathJax-118-QINU
さらにUNIQ2cca723c10bf8fe1-MathJax-119-QINUの線形性から
UNIQ2cca723c10bf8fe1-MathJax-120-QINU
UNIQ2cca723c10bf8fe1-MathJax-121-QINUが最大で,(3)のように各UNIQ2cca723c10bf8fe1-MathJax-122-QINUは正の数(UNIQ2cca723c10bf8fe1-MathJax-123-QINU)であるから,
UNIQ2cca723c10bf8fe1-MathJax-124-QINU
さらに,(2)から
UNIQ2cca723c10bf8fe1-MathJax-125-QINU
で
UNIQ2cca723c10bf8fe1-MathJax-126-QINU
となる。結局,関数UNIQ2cca723c10bf8fe1-MathJax-127-QINUの制約条件を表す凸多角形の内部(境界を含む)の点全てを調べる必要がなく、
頂点での関数UNIQ2cca723c10bf8fe1-MathJax-128-QINUの値を調べれば良いことが判る.
UNIQ2cca723c10bf8fe1-MathJax-129-QINU式のように変数に関する制約条件式が1次式で与えられ, UNIQ2cca723c10bf8fe1-MathJax-130-QINU式のように評価関数も1次式で与えられる問題は線形計画法と呼ばれる.
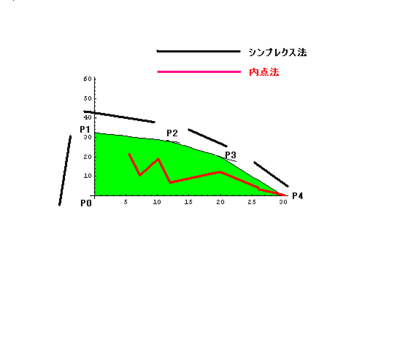
線形化計画法の代表的な解法であるシンプレクス法は,制約条件を表す凸多角形の頂点での 関数UNIQ2cca723c10bf8fe1-MathJax-131-QINUの値を効率的に調べる方法である。 適当な,頂点から始め,関数UNIQ2cca723c10bf8fe1-MathJax-132-QINUの値が増大する頂点へ次々移動して,最大解を探す.
この他に,凸多角形の内部の点から,最大解を与える頂点を探索する内点法もある。
線形計画法(2)
例題2
ある企業では製品A,B,Cを原料Ⅰ,Ⅱ,Ⅲ,Ⅳ用いて生産している. 製品A,B,C の1単位当たり利益をそれぞれ80,110,95とする. また, 製品A,B,Cを1単位生産するのに必要な原料Ⅰ,Ⅱ,Ⅲ,Ⅳのそれぞれ量と使用可能な上限が次の表で与えられる. これらの条件のもとに,利益を最大にするには製品A,B,Cをそれぞれ,どれだけ生産すれば良いか?.
| 原材\製品名 | A | B | C | 使用できる上限 |
| Ⅰ | 4 | 0 | 7 | 90 |
| Ⅱ | 1 | 3 | 9 | 60 |
| Ⅲ | 6 | 0 | 14 | 110 |
| Ⅳ | 4 | 10 | 1 | 75 |
この問題も例題1と同じように以下のように数学的に定式化される.
製品A,B,CをそれぞれUNIQ2cca723c10bf8fe1-MathJax-133-QINU 単位生産するときUNIQ2cca723c10bf8fe1-MathJax-134-QINUは以下の不等式を満たす.
UNIQ2cca723c10bf8fe1-MathJax-135-QINU
さらに各製品生産量は負ではないから
UNIQ2cca723c10bf8fe1-MathJax-136-QINU
この制約条件のもとに
UNIQ2cca723c10bf8fe1-MathJax-137-QINU
を最大にするUNIQ2cca723c10bf8fe1-MathJax-138-QINUを求めよ.
この問題の解法にはシンプレックス法や内点法がある.
シンプレクス法は[菅沼]の解説が判りやすい.
この問題を解くのにはMicrosoft Excelのソルバーや
フリーソフトのOpen Office で提供されるソルバーと同等の機能をもつソフトを用いることができる.
この問題のMicrosoft Excelのソルバーによる解法例を示す。
Microsoft Excelのソルバー を用いる.
- ソルバーの導入
- Excel の メニュー「データ」に「分析」「ソルバー」がある場合は以下の手続きは不要である.
そのままソルバーによる解法の例を実行する.
- Excelのメニュー「データ」に「分析」「ソルバー」がない場合
- ファイル > オプション > アドイン の順に選択
- アドインの表示窓 アクティブでないアプリケーションにExcelソルバー があることを確認
- 画面下の管理(A)と表示される小さい窓のドロップダウンリスト▼でExcelアドインを選択後,設定(G)をクリック
- 有効なアドインが小窓で表示される. その中のソルバーアドインを選択しチェックを入れ[OK]をクリックする.
- ソルバーによる解法の例
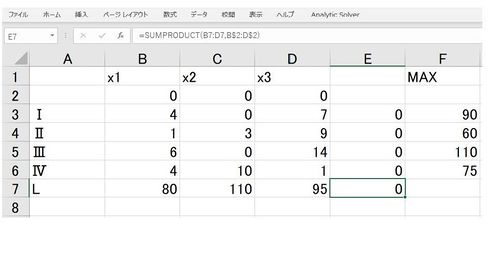
- Excelに下記の作成例のように表1のデータを作成する.
この作成例では
セル B2,C2,D2 が 製品A,B,Cのそれぞれの生産量
UNIQ2cca723c10bf8fe1-MathJax-139-QINUを表す.
- 線形の一次式
UNIQ2cca723c10bf8fe1-MathJax-140-QINU
をE3, E4, E5, E6に入力している.
ここで,sumproduct(B4:D4,BUNIQ2cca723c10bf8fe1-MathJax-141-QINU2)はベクトル(B4,C4,D4) と(B2,C2,D2)の内積 B4*B2+C4*C2+D4*D2 でありUNIQ2cca723c10bf8fe1-MathJax-142-QINU を表す.
- F3,F4, F5, F6には,原材料Ⅰ,Ⅱ,Ⅲ,Ⅳの使用できる量の上限を入力している.
- E7には
UNIQ2cca723c10bf8fe1-MathJax-143-QINU
を表す式を入力している.
- 表のデータを入力後,
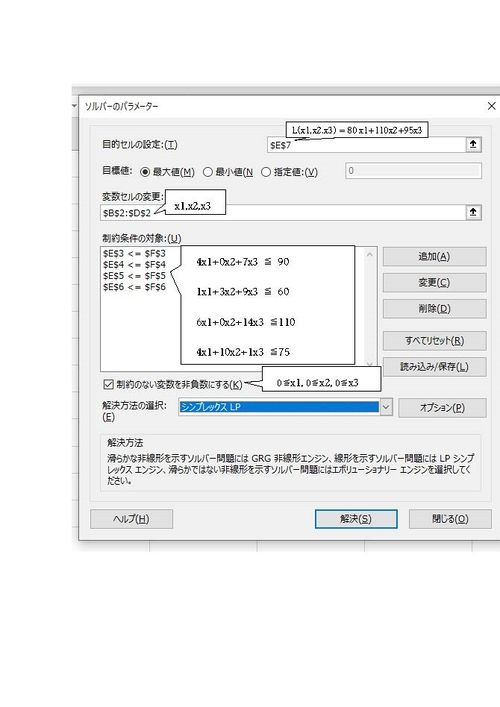
- メニュー 「データ」,「分析」,「ソルバー」の順にクリックしてソルバーのパラメータ入力用の窓を開く.
- 表のデータを入力後,
- 目的の設定という欄にセルE7を指定する
- 目標値には「最大値」を選択し,チェックを入れる.
- 変数セルの変更欄にはx_1,x_2,x_3を表すセルB2からD2をドラックして指定する.
- 制約条件の対象の欄には
この例題の制約条件式
UNIQ2cca723c10bf8fe1-MathJax-144-QINU
を表す式を入力する. このためには,入力窓の「追加」をクリックし制約条件の追加入力用の窓を表示させ, 例えば
UNIQ2cca723c10bf8fe1-MathJax-145-QINU
を表す式を入力するのであればセルの参照欄にUNIQ2cca723c10bf8fe1-MathJax-146-QINUを表すセルE3を指定 ≦,=,≧などのドロップダウンリストで≦を選択し,制約条件の欄には上限値の90を入力する.入力後さらに「追加」をクリックし他の3つの制約条件式も同様に入力する.
- さらに, 制約条件式
UNIQ2cca723c10bf8fe1-MathJax-147-QINU を入力するため
「制約のない変数を非負数にする」 にチェックを入れる.
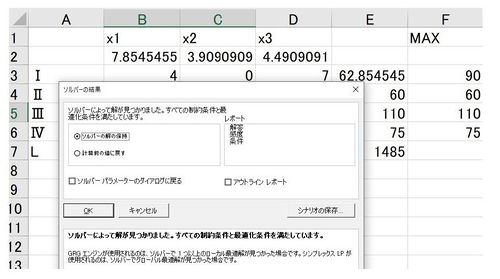
- 最後に「解決」をクリックすると以下の結果が出力される.
UNIQ2cca723c10bf8fe1-MathJax-148-QINU
のときに
UNIQ2cca723c10bf8fe1-MathJax-149-QINU
が最大値1485をもつことを表す.制約条件は満たされている.
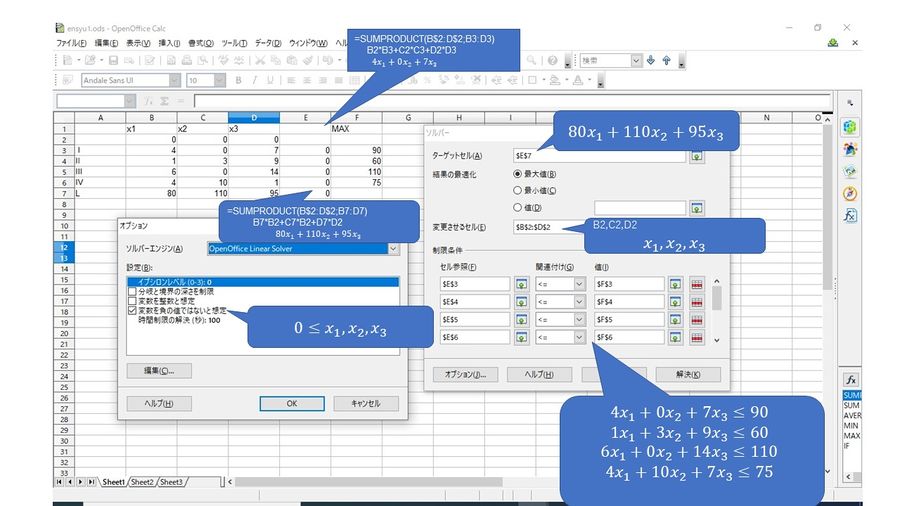
フリーソフトOpenOfficeの表計算(Calc) でも同様に解くことができる.
Calcの線形計画法解析ソフトもExcelと同じ名前の「ソルバー」である. メニューの「ツール」の「ソルバー」である. Excelのソルバーと操作法は殆ど同じある.
ベクトルの内積もExcelと同様にsumproductである. 行ベクトルと行ベクトルとの区切りが,ではなく;であることが異なる。 ベクトル(B4,C4,D4) と(B2,C2,D2)の内積 B4*B2+C4*C2+D4*D2 はsumproduct(B4:D4;B2:D2)で表される. また,
制約条件式
UNIQ2cca723c10bf8fe1-MathJax-150-QINU を入力するためには,ソルバーのメニューのオプションを使う. 変数を負でない という 選択にチェックを入れる.
以下にデータの入力とソルバーの設定例を示す.