物理/運動の法則の応用2
提供: Internet Web School
目次
|
解説
この節では複数の質点が集まって作る質点系と、硬くて形を変えない質点系である剛体の運動を、運動法則を用いて解析しよう。
質点系の運動
2個以上の質点が集まって出来ている系を質点系という。
質点系というときは、各質点は密集していても、離れ離れでも良い。互いに固着しようが、自由に動けようが構わない。
すべての物質は、分子の集合と考えたり、細分化して極小部分に分け、それらの集合と考えれば、十分な精度で、質点系とみなすことができる。
そのため質点系の運動の法則を、ニュートンの運動法則から導出すれば、その応用範囲は非常に広い。
質点系の運動と重心
系の任意の２つの質点間には作用・反作用の法則を満たす力が働いていてもよい。
この力を質点系の”内力”という。
質点系の各質点に外部から力（外力という）が加わる時、この質点系はどんな運動をするだろうか。
質点系の各質点の位置をUNIQ473e03fe1938e82e-MathJax-762-QINU、質量をUNIQ473e03fe1938e82e-MathJax-763-QINUとし、
質点UNIQ473e03fe1938e82e-MathJax-764-QINU に作用する外力をUNIQ473e03fe1938e82e-MathJax-765-QINU、
UNIQ473e03fe1938e82e-MathJax-766-QINU に、他の質点UNIQ473e03fe1938e82e-MathJax-767-QINUから作用する内力をUNIQ473e03fe1938e82e-MathJax-768-QINUとする(UNIQ473e03fe1938e82e-MathJax-769-QINU)。
すると、各質点に対して、運動の第２法則により、
UNIQ473e03fe1938e82e-MathJax-770-QINU UNIQ473e03fe1938e82e-MathJax-771-QINU ここでUNIQ473e03fe1938e82e-MathJax-772-QINU、
各ベクトルを自由ベクトルとみなしてUNIQ473e03fe1938e82e-MathJax-773-QINUについて加え合わせると、UNIQ473e03fe1938e82e-MathJax-774-QINUなので、
UNIQ473e03fe1938e82e-MathJax-775-QINU
が得られる。
質点系の全質量UNIQ473e03fe1938e82e-MathJax-776-QINUと質点系に働く全外力UNIQ473e03fe1938e82e-MathJax-777-QINUを用いて書きなおすと、
UNIQ473e03fe1938e82e-MathJax-778-QINU
質点系の重心UNIQ473e03fe1938e82e-MathJax-779-QINUを UNIQ473e03fe1938e82e-MathJax-780-QINU で定義すると、
UNIQ473e03fe1938e82e-MathJax-781-QINU
この式は、力UNIQ473e03fe1938e82e-MathJax-782-QINUをうける質量UNIQ473e03fe1938e82e-MathJax-783-QINUの質点の運動方程式と同じである。
以下の解説も参考にしてください。
複雑にみえる運動も重心の運動をみれば簡単である
体操選手の運動は、跳躍などで空中をまいながら、回転や体の屈伸、ひねりなどを行う。大変複雑で美しい。
しかし、導出した質点系の重心の運動法則から、体の重心の運動は、投射体の運動であり、放物線をえがいて移動することが分かる。
空中に飛び出た瞬間の重心の位置と速度(速さと方向・向き）で、その軌跡は完全に決まってしまうのである。
剛体の運動とつり合い
剛体
剛体(Rigid body)とは、
質点系であって、それらの、どの2質点の間の距離も変わらない,特殊な質点系のことを言う。
どの2質点の間の距離も変わらなければ変形は起こらない。
固くて変形しにくい物体を理想化した概念である。
剛体の運動
剛体は変形しない質点系なので、その運動は、重心の運動と、重心の周りの回転運動を合成したものになる。
重心の運動は前の節で説明したように、質点の運動と同じように簡単に扱える。
重心の周りの回転運動について解析するには、少し難しい数学が必要になる。
- ウィキペディア（剛体の力学）を参照のこと。
このテキストでは、固定軸の周りの回転運動を中心に、 剛体運動の初歩と釣合の条件について学ぶ。
固定軸のまわりの回転運動
剛体が、剛体の中を通る固定軸の周りを回転する運動（車輪の回転など）を考える。
応用も考え、回転軸は重心を通らなくてもよいように一般化しておく。
（注）なお、軸が動かないようにするためには軸受が必要である。
工夫しても回転時に軸は軸受から多少の摩擦力を受け、回転にブレーキがかかる。
しかし、これは無視出来るほど小さいと仮定する。
すると軸が受ける力は、軸の変動を防ぎ、固定軸の周りの運動に限定させる作用を持ち、
回転を遅める作用は持たないことになる。
回転運動の表示法
固定軸まわりの剛体の運動はどのように表示したらよいだろうか。
・剛体の位置を表す変数；回転角
剛体が幾ら回転したか分かるように、剛体の、回転軸上にない一点UNIQ473e03fe1938e82e-MathJax-784-QINUに印を付ける。
次に、角度を測る基準線をきめるため、座標系を決めよう。
UNIQ473e03fe1938e82e-MathJax-785-QINUから固定軸へ垂線をひき、その足を原点UNIQ473e03fe1938e82e-MathJax-786-QINUとし,固定軸をｚ座標とする(静止した)３次元直交座標UNIQ473e03fe1938e82e-MathJax-787-QINUを考える。
剛体が固定軸の周りを回転すると、印UNIQ473e03fe1938e82e-MathJax-788-QINUはxy平面上を、原点UNIQ473e03fe1938e82e-MathJax-789-QINUを中心に円を描いて動くことになる。
その位置ベクトルUNIQ473e03fe1938e82e-MathJax-790-QINUがx軸の正方向となす角度UNIQ473e03fe1938e82e-MathJax-791-QINUを、回転角と呼ぶ。図参照。
但し、x軸から反時計回りの角を正にする。
また一回転した後ならば、一回転の角UNIQ473e03fe1938e82e-MathJax-792-QINUを加え、逆周りに一回転した後ならUNIQ473e03fe1938e82e-MathJax-793-QINUを引き、
角度だけでなく回転数も分かるようにする。
回転角が指定されると、点UNIQ473e03fe1938e82e-MathJax-794-QINUの位置が決まる。
それだけでなく剛体は変形しないので、剛体のすべての点の位置がきまる。
そこで回転角UNIQ473e03fe1938e82e-MathJax-795-QINUの時間変化UNIQ473e03fe1938e82e-MathJax-796-QINUを明らかにすれば、剛体の回転運動は定まる。
固定軸のまわりの回転運動において回転角の果たし役割は、質点の運動において質点の位置が果たし役割に対応していることが分かる。
・回転の角速度と角加速度
UNIQ473e03fe1938e82e-MathJax-797-QINUを時間で微分したUNIQ473e03fe1938e82e-MathJax-798-QINUを回転の角速度と呼ぶ。
直観的には、時刻UNIQ473e03fe1938e82e-MathJax-799-QINUの瞬間の、回転の速さ（回転角の時間に対する変化率）を表す。
さらにもう一回時間微分したUNIQ473e03fe1938e82e-MathJax-800-QINUを回転の角加速度と呼ぶ。
回転力(トルク）
質点の運動に倣って、剛体に作用する力によって、その位置(＝回転角）がどう変化するかの法則を導出したい。
しかし、剛体の回転の場合、ある方向の力は、剛体の回転に全く関係しない。
例えば、回転軸から放射状にでる半直線方向の力は全く回転の変化に寄与しない。
そこで剛体の回転を変化させる力とはなにかという問題から考察する必要が起こる。
質点運動における力の定義(力と運動量の変化の関係）や力と仕事の関係など力の係っている式のなかから、
剛体の回転運動に容易に拡張出来るものを選び、その式から、回転に関する力を求めることを試みる。
力の定義からは、回転運動への拡張を、推測することは難しい。
力と仕事の関係の考察をしてみよう。
力と仕事の関係からの考察
適当な直交座標系をさだめ、ベクトルは、座標成分で表示する。
質点に、一定の力UNIQ473e03fe1938e82e-MathJax-801-QINUを作用させて、x軸方向に変位させる。
質点はこの軸の上でしか動けないように拘束され、摩擦はないと仮定する。
質点の変位ベクトルは一次元の変数UNIQ473e03fe1938e82e-MathJax-802-QINUを使ってUNIQ473e03fe1938e82e-MathJax-803-QINUと表せる。
すると力のなす仕事は、UNIQ473e03fe1938e82e-MathJax-804-QINUである。
逆に物体に一定の力を加え、x軸上でUNIQ473e03fe1938e82e-MathJax-805-QINUだけ変位させた時の仕事UNIQ473e03fe1938e82e-MathJax-806-QINUが分かれば、質点を動かした力は
UNIQ473e03fe1938e82e-MathJax-807-QINU
で求められる。
UNIQ473e03fe1938e82e-MathJax-808-QINUは、質点をx軸上で動かすことには全く寄与せず、
x軸に拘束された質点を動かす力は、UNIQ473e03fe1938e82e-MathJax-809-QINUなのである。
固定軸まわりの回転もその変位は一次元の変数である回転角度で表わせるので、
これに倣って、
UNIQ473e03fe1938e82e-MathJax-810-QINU回転した角度
を、回転にかんする力であると考える。これを回転力と呼ぶ。トルクともいう。
この方針を実行して回転力を具体的に求めよう。
剛体に力を加え微小角動かす時の、力のなす仕事の算出
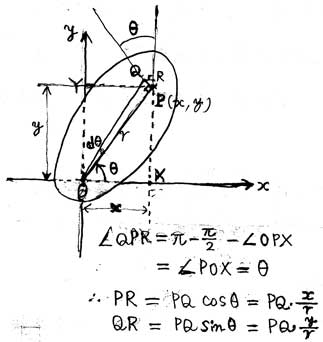
図4.1のように剛体の任意の一点UNIQ473e03fe1938e82e-MathJax-811-QINUを考える。
z座標の上方からxy平面を見下ろしているので、ｚ座標は点になりUNIQ473e03fe1938e82e-MathJax-812-QINUと書いてある。
まず一点UNIQ473e03fe1938e82e-MathJax-813-QINUに力UNIQ473e03fe1938e82e-MathJax-814-QINUが作用して、微小角UNIQ473e03fe1938e82e-MathJax-815-QINUだけ回転したときの
仕事UNIQ473e03fe1938e82e-MathJax-816-QINUを計算し回転力を求めよう。
UNIQ473e03fe1938e82e-MathJax-817-QINU点から回転軸（ｚ軸）に垂線を下ろし、その足をUNIQ473e03fe1938e82e-MathJax-818-QINUとする。
UNIQ473e03fe1938e82e-MathJax-819-QINUの長さをUNIQ473e03fe1938e82e-MathJax-820-QINU、x軸となす角をUNIQ473e03fe1938e82e-MathJax-821-QINU(ラジアン)と置く。
この角度は、
剛体につけた印の位置ベクトルUNIQ473e03fe1938e82e-MathJax-822-QINUがｘ軸となす回転角UNIQ473e03fe1938e82e-MathJax-823-QINUと
このベクトルとUNIQ473e03fe1938e82e-MathJax-824-QINU（をｘｙ平面に平行移動したベクトル）の間の角の和である。
後者は、剛体なので、運動しても変わらない定数である。そこで、UNIQ473e03fe1938e82e-MathJax-825-QINU定数,と書ける。
剛体がｚ軸の周りを微小角UNIQ473e03fe1938e82e-MathJax-826-QINU回転して、点UNIQ473e03fe1938e82e-MathJax-827-QINUが図の点UNIQ473e03fe1938e82e-MathJax-828-QINUに移動したとする。
すると角UNIQ473e03fe1938e82e-MathJax-829-QINUはほぼ直角（=UNIQ473e03fe1938e82e-MathJax-830-QINU）でUNIQ473e03fe1938e82e-MathJax-831-QINUの長さUNIQ473e03fe1938e82e-MathJax-832-QINUは、UNIQ473e03fe1938e82e-MathJax-833-QINU。
UNIQ473e03fe1938e82e-MathJax-834-QINUのｘ成分とｙ成分は、図4－１中に示したように、それぞれ、UNIQ473e03fe1938e82e-MathJax-835-QINU、UNIQ473e03fe1938e82e-MathJax-836-QINU。
UNIQ473e03fe1938e82e-MathJax-837-QINUを代入すると、
UNIQ473e03fe1938e82e-MathJax-838-QINU、UNIQ473e03fe1938e82e-MathJax-839-QINU、UNIQ473e03fe1938e82e-MathJax-840-QINU
点UNIQ473e03fe1938e82e-MathJax-841-QINUに作用する力UNIQ473e03fe1938e82e-MathJax-842-QINUが、物体をUNIQ473e03fe1938e82e-MathJax-843-QINUだけ動かしたので、
その仕事は、UNIQ473e03fe1938e82e-MathJax-844-QINU（内積）。
この右辺を内積の性質を用いて座標成分で表すと、
UNIQ473e03fe1938e82e-MathJax-845-QINU
UNIQ473e03fe1938e82e-MathJax-846-QINU
ｚ軸まわりの回転力の導出
ゆえに、力UNIQ473e03fe1938e82e-MathJax-847-QINUのｚ軸まわりの回転力（トルク）UNIQ473e03fe1938e82e-MathJax-848-QINUはUNIQ473e03fe1938e82e-MathJax-849-QINU
に等しい。
これより、UNIQ473e03fe1938e82e-MathJax-850-QINUが得られる。
この式と、直線上に拘束された質点の運動における、力と仕事の関係式( 節 項）と対比させると、
UNIQ473e03fe1938e82e-MathJax-851-QINU は、拘束された直線の上を動かすときに、働いた力の成分が対応し、
UNIQ473e03fe1938e82e-MathJax-852-QINU は、変位量 に対応していることが分かる。
ｚ軸まわりの回転力（トルク）の性質
(1)力UNIQ473e03fe1938e82e-MathJax-853-QINUのｚ軸まわりの回転力は,UNIQ473e03fe1938e82e-MathJax-854-QINUには関係しない。
言いかえるとz軸を固定軸とする剛体にｚ軸の方向の力を加えても、ｚ軸の周りの回転は起こらない。
(2)剛体の１点UNIQ473e03fe1938e82e-MathJax-855-QINUに作用する力UNIQ473e03fe1938e82e-MathJax-856-QINUを考える。
点UNIQ473e03fe1938e82e-MathJax-857-QINUからｚ軸に下ろした垂線の足をUNIQ473e03fe1938e82e-MathJax-858-QINUと書く。
力UNIQ473e03fe1938e82e-MathJax-859-QINUを、,
UNIQ473e03fe1938e82e-MathJax-860-QINU方向の成分UNIQ473e03fe1938e82e-MathJax-861-QINUと、
ｚ軸まわりの回転によりUNIQ473e03fe1938e82e-MathJax-862-QINUの描く、UNIQ473e03fe1938e82e-MathJax-863-QINUを中心とする回転円の（左回りの）接線方向の成分UNIQ473e03fe1938e82e-MathJax-864-QINU
および、これら２成分に直交する成分(ｚ軸と平行)
に分解する(図参照）。この時、
・力UNIQ473e03fe1938e82e-MathJax-865-QINUのｚ軸まわりの回転力は、零である。
すなわち、動径方向の力は回転に寄与しない。
・力UNIQ473e03fe1938e82e-MathJax-866-QINUのｚ軸まわりの回転力は、UNIQ473e03fe1938e82e-MathJax-867-QINUのｚ軸まわりの回転力に等しい。
数式で表すと、UNIQ473e03fe1938e82e-MathJax-868-QINU
(3)剛体に作用する力の作用点を、力の作用線上で動かす限り、回転力は変化しない。
ここで、力の作用線とは、力の作用点を通り、力の方向と重なる直線のこと。
これらはいずれも直観と合致する。
証明は、試みてほしい。
他の軸の周りの回転力
力UNIQ473e03fe1938e82e-MathJax-869-QINUのｘ軸、y軸まわりの回転力も同様に計算できる。結果は、
x軸まわりの回転力；UNIQ473e03fe1938e82e-MathJax-870-QINU
y軸まわりの回転力；UNIQ473e03fe1938e82e-MathJax-871-QINU
原点まわりの力のモーメント
位置ベクトルUNIQ473e03fe1938e82e-MathJax-872-QINUの剛体の点UNIQ473e03fe1938e82e-MathJax-873-QINUに作用する力UNIQ473e03fe1938e82e-MathJax-874-QINUの原点まわりの力のモーメントを、
UNIQ473e03fe1938e82e-MathJax-875-QINUx軸まわりのトルク、y軸まわりのトルク、z軸まわりのトルクUNIQ473e03fe1938e82e-MathJax-876-QINUで定義する。
数式で書くと、
UNIQ473e03fe1938e82e-MathJax-877-QINU,
ベクトル積と力のモーメントのベクトル積表示
以上の結果は、ベクトル積（クロス積ともいう）を用いると簡潔、正確に表現でき、
回転運動の性質を調べるのが容易になる。
3次元ベクトルUNIQ473e03fe1938e82e-MathJax-878-QINU のベクトル積UNIQ473e03fe1938e82e-MathJax-879-QINUとは、3次元ベクトルであり,
大きさはUNIQ473e03fe1938e82e-MathJax-880-QINU を2辺とする平行四辺形の面積に等しく、
方向はこの四辺形に垂直で、向きは、UNIQ473e03fe1938e82e-MathJax-881-QINUが右手系をなすように定めたものである。
すると、ベクトル積に関して以下の8つの命題が成り立つ。
ベクトル積にかんする命題
以下に述べる全ての命題で、
UNIQ473e03fe1938e82e-MathJax-882-QINUは3次元ベクトル
UNIQ473e03fe1938e82e-MathJax-883-QINUは実数とする。
命題１．
UNIQ473e03fe1938e82e-MathJax-884-QINU を, UNIQ473e03fe1938e82e-MathJax-885-QINUと垂直な成分UNIQ473e03fe1938e82e-MathJax-886-QINU と,平行な成分UNIQ473e03fe1938e82e-MathJax-887-QINU の和に分解するとき、
UNIQ473e03fe1938e82e-MathJax-888-QINU
UNIQ473e03fe1938e82e-MathJax-889-QINU
命題２．
UNIQ473e03fe1938e82e-MathJax-890-QINU
命題３
UNIQ473e03fe1938e82e-MathJax-891-QINU
命題４．
UNIQ473e03fe1938e82e-MathJax-892-QINU
命題４の系
UNIQ473e03fe1938e82e-MathJax-893-QINU
UNIQ473e03fe1938e82e-MathJax-894-QINU
命題５．
UNIQ473e03fe1938e82e-MathJax-895-QINU を
それぞれ大きさ(長さ)１で互いに直交し、右手系をなす、ベクトル(右手系をなす正規直交基底)とする。
この時、
UNIQ473e03fe1938e82e-MathJax-896-QINU
命題６．
ベクトルUNIQ473e03fe1938e82e-MathJax-897-QINUを,命題５で用いた基底UNIQ473e03fe1938e82e-MathJax-898-QINU で決まる座標の座標成分で表示しておく。
するとUNIQ473e03fe1938e82e-MathJax-899-QINU
命題７．
UNIQ473e03fe1938e82e-MathJax-900-QINU
命題８．
UNIQ473e03fe1938e82e-MathJax-901-QINU と UNIQ473e03fe1938e82e-MathJax-902-QINUを,UNIQ473e03fe1938e82e-MathJax-903-QINUにかんして微分可能な、ベクトルに値をとる関数とする。すると、
UNIQ473e03fe1938e82e-MathJax-904-QINU は、UNIQ473e03fe1938e82e-MathJax-905-QINUにかんして微分可能で、
UNIQ473e03fe1938e82e-MathJax-906-QINU
これらの証明は、後節で扱う。 ベクトル積に関しては以下を参照のこと。
力のモーメントのベクトル積表示
ベクトル積の命題６を用いると、
位置ベクトルUNIQ473e03fe1938e82e-MathJax-907-QINUの点に作用するUNIQ473e03fe1938e82e-MathJax-908-QINU の
原点まわりの力のモーメントは、UNIQ473e03fe1938e82e-MathJax-909-QINU
x軸まわりの回転力(トルク）は、UNIQ473e03fe1938e82e-MathJax-910-QINU と表せることが分かる。
ｙ軸とｚ軸周りの回転力も、それぞれ
UNIQ473e03fe1938e82e-MathJax-911-QINU ,UNIQ473e03fe1938e82e-MathJax-912-QINUで
表せる。
力のモーメントの性質
もっと一般に、どんな軸の周りの回転力も、UNIQ473e03fe1938e82e-MathJax-913-QINU から得られる。
定理；
UNIQ473e03fe1938e82e-MathJax-914-QINUを、原点を始点とする大きさ１の任意のベクトルとする。
すると、
UNIQ473e03fe1938e82e-MathJax-915-QINU UNIQ473e03fe1938e82e-MathJax-916-QINUは、力UNIQ473e03fe1938e82e-MathJax-917-QINUのUNIQ473e03fe1938e82e-MathJax-918-QINU軸の周りの回転力になる。式で書くと、UNIQ473e03fe1938e82e-MathJax-919-QINU
この式を、回転力の定義に基づいて言い換えると、
力UNIQ473e03fe1938e82e-MathJax-920-QINUのもとで、剛体をUNIQ473e03fe1938e82e-MathJax-921-QINU軸の右まわりに角度UNIQ473e03fe1938e82e-MathJax-922-QINUだけ回転させたとき、
UNIQ473e03fe1938e82e-MathJax-923-QINUのなす仕事UNIQ473e03fe1938e82e-MathJax-924-QINUは、UNIQ473e03fe1938e82e-MathJax-925-QINU
証明；
９つに分けて示す。
ⅰ）準備
図のように、剛体の点 UNIQ473e03fe1938e82e-MathJax-926-QINU から、UNIQ473e03fe1938e82e-MathJax-927-QINU 軸に垂線を下ろし、その足を UNIQ473e03fe1938e82e-MathJax-928-QINU とする。
力 UNIQ473e03fe1938e82e-MathJax-929-QINU のもとで、剛体が UNIQ473e03fe1938e82e-MathJax-930-QINU を固定軸にして、
微小時間に、微小角UNIQ473e03fe1938e82e-MathJax-931-QINU だけ回転したとする。
このとき、UNIQ473e03fe1938e82e-MathJax-932-QINU が移った先を、UNIQ473e03fe1938e82e-MathJax-933-QINU とする。
ⅱ）回転角 UNIQ473e03fe1938e82e-MathJax-934-QINU が微小なので、
この回転中の UNIQ473e03fe1938e82e-MathJax-935-QINU の軌跡(円弧の微小部分）は、有向線分UNIQ473e03fe1938e82e-MathJax-936-QINU で精度高く、近似できる。
ⅲ）この間に力 UNIQ473e03fe1938e82e-MathJax-937-QINU がなした仕事 UNIQ473e03fe1938e82e-MathJax-938-QINU は、UNIQ473e03fe1938e82e-MathJax-939-QINU
この仕事を、回転角UNIQ473e03fe1938e82e-MathJax-940-QINUで割ると、力の UNIQ473e03fe1938e82e-MathJax-941-QINU 軸周りの回転力が得られる。そこで、UNIQ473e03fe1938e82e-MathJax-942-QINU を、この定理で与えられている諸量を使って表現し、これを用いて、仕事を計算しよう。
ⅳ）有向線分UNIQ473e03fe1938e82e-MathJax-943-QINUの方向を求める。
UNIQ473e03fe1938e82e-MathJax-944-QINU は、UNIQ473e03fe1938e82e-MathJax-945-QINU 軸と垂直でUNIQ473e03fe1938e82e-MathJax-946-QINU を通る平面UNIQ473e03fe1938e82e-MathJax-947-QINU上にあり、
UNIQ473e03fe1938e82e-MathJax-948-QINUを中心とする円の弧の微小部分をなすので、線分UNIQ473e03fe1938e82e-MathJax-949-QINU と直交する。UNIQ473e03fe1938e82e-MathJax-950-QINU
また、UNIQ473e03fe1938e82e-MathJax-951-QINU 軸と垂直でUNIQ473e03fe1938e82e-MathJax-952-QINU を通る平面UNIQ473e03fe1938e82e-MathJax-953-QINU上にあるので、
UNIQ473e03fe1938e82e-MathJax-954-QINUはUNIQ473e03fe1938e82e-MathJax-955-QINU 軸とも直交し、従って線分UNIQ473e03fe1938e82e-MathJax-956-QINUと直交する。UNIQ473e03fe1938e82e-MathJax-957-QINU
ゆえに、UNIQ473e03fe1938e82e-MathJax-958-QINU は、３点O,Q,Pを通る平面 UNIQ473e03fe1938e82e-MathJax-959-QINU と直交する。
すると、UNIQ473e03fe1938e82e-MathJax-960-QINU は、平面 UNIQ473e03fe1938e82e-MathJax-961-QINU 上のすべての線分と直交する。
ゆえに、UNIQ473e03fe1938e82e-MathJax-962-QINU,UNIQ473e03fe1938e82e-MathJax-963-QINU
これで、UNIQ473e03fe1938e82e-MathJax-964-QINU の方向は、求まった。
ⅴ）有向線分UNIQ473e03fe1938e82e-MathJax-965-QINU の向き
点 UNIQ473e03fe1938e82e-MathJax-966-QINU は、UNIQ473e03fe1938e82e-MathJax-967-QINU 軸の周りを右周りに回転するので、その向きは、
UNIQ473e03fe1938e82e-MathJax-968-QINU と同じ向きである。
ⅵ）UNIQ473e03fe1938e82e-MathJax-969-QINU の大きさ。
UNIQ473e03fe1938e82e-MathJax-970-QINUは、 UNIQ473e03fe1938e82e-MathJax-971-QINU を中心とする、半径 UNIQ473e03fe1938e82e-MathJax-972-QINU の円弧の一部なので、
その中心角UNIQ473e03fe1938e82e-MathJax-973-QINU を用いて、UNIQ473e03fe1938e82e-MathJax-974-QINU
ⅶ）ⅳ）、ⅴ）、ⅵ）から
UNIQ473e03fe1938e82e-MathJax-975-QINU
ⅷ）UNIQ473e03fe1938e82e-MathJax-976-QINUが成り立つ。
なぜなら、
UNIQ473e03fe1938e82e-MathJax-977-QINU ,ここで UNIQ473e03fe1938e82e-MathJax-978-QINU はUNIQ473e03fe1938e82e-MathJax-979-QINU とUNIQ473e03fe1938e82e-MathJax-980-QINU の間の角。
この式をⅶ)で得られた式に代入すれば、所望の結果が得られる。
ⅸ）UNIQ473e03fe1938e82e-MathJax-981-QINU
ⅹ）UNIQ473e03fe1938e82e-MathJax-982-QINU
定理の証明終わり。
（注）剛体が固定軸の周りでなく、自由に回転するときでも、
ある瞬間には、ある軸の周りの回転になっている。
力のモーメントは、どんな軸周りの回転力の情報も含んでいることが証明されたので、
回転運動一般に有効な概念であることが分かる。
剛体の複数個所に作用する力の回転力
次に剛体の多くの点に力を加えたときの回転力を求めよう。
力の作用点をUNIQ473e03fe1938e82e-MathJax-983-QINU、力をUNIQ473e03fe1938e82e-MathJax-984-QINUとする。
これらの力のもとで剛体がz軸まわりをUNIQ473e03fe1938e82e-MathJax-985-QINUだけ微小回転するときの、各力のなす仕事の合計は、
UNIQ473e03fe1938e82e-MathJax-986-QINU
従って、作用点UNIQ473e03fe1938e82e-MathJax-987-QINUの力UNIQ473e03fe1938e82e-MathJax-988-QINUの全体がもつz軸まわりの回転力は、
UNIQ473e03fe1938e82e-MathJax-989-QINU ここでUNIQ473e03fe1938e82e-MathJax-990-QINUは力UNIQ473e03fe1938e82e-MathJax-991-QINUのｚ軸まわりの回転力。
同様に、x軸まわりとy軸まわりの回転力も、それぞれ
UNIQ473e03fe1938e82e-MathJax-992-QINU
UNIQ473e03fe1938e82e-MathJax-993-QINU
力UNIQ473e03fe1938e82e-MathJax-994-QINUの原点周りに力のモーメントUNIQ473e03fe1938e82e-MathJax-995-QINUはUNIQ473e03fe1938e82e-MathJax-996-QINUで定義した。
全ての力の原点周りの力のモーメントも、同様に
UNIQ473e03fe1938e82e-MathJax-997-QINUで定義する。すると、
UNIQ473e03fe1938e82e-MathJax-998-QINU
全ての力の原点周りの力のモーメントUNIQ473e03fe1938e82e-MathJax-999-QINUも、上述の定理と同様の定理(定理の系と呼ぶ）が成り立つ。
定理の系
UNIQ473e03fe1938e82e-MathJax-1000-QINUを剛体に作用する全ての力のモーメントとし、
UNIQ473e03fe1938e82e-MathJax-1001-QINUを、原点を始点とする大きさ１の任意のベクトルとする。
すると、
UNIQ473e03fe1938e82e-MathJax-1002-QINU UNIQ473e03fe1938e82e-MathJax-1003-QINUは、力UNIQ473e03fe1938e82e-MathJax-1004-QINUのUNIQ473e03fe1938e82e-MathJax-1005-QINU軸の周りの回転力になる。
式で書くと、UNIQ473e03fe1938e82e-MathJax-1006-QINU
この式を、回転力の定義に基づいて言い換えると、
力UNIQ473e03fe1938e82e-MathJax-1007-QINUのもとで、剛体をUNIQ473e03fe1938e82e-MathJax-1008-QINU軸の右まわりに角度UNIQ473e03fe1938e82e-MathJax-1009-QINUだけ回転させたとき、
これらの力のなす仕事UNIQ473e03fe1938e82e-MathJax-1010-QINUは、UNIQ473e03fe1938e82e-MathJax-1011-QINU
この系は、内積の性質を使えば、定理から、容易に導かれる。
質点系に作用する重力のモーメント
ｎ個の質点系を考える。
第ｉ質点の質量をUNIQ473e03fe1938e82e-MathJax-1012-QINU、位置ベクトルをUNIQ473e03fe1938e82e-MathJax-1013-QINUとする。
鉛直上方をｚ軸の正方向とする直交座標系UNIQ473e03fe1938e82e-MathJax-1014-QINUをいれる。
この質点系に作用する重力の原点周りのモーメントUNIQ473e03fe1938e82e-MathJax-1015-QINUを求めよう。
第ｉ質点に働く重力は、
UNIQ473e03fe1938e82e-MathJax-1016-QINU
なので、
UNIQ473e03fe1938e82e-MathJax-1017-QINU
UNIQ473e03fe1938e82e-MathJax-1018-QINU
すでに学んだことから、この質点系の重心は、
UNIQ473e03fe1938e82e-MathJax-1019-QINU
であった。ここで、 UNIQ473e03fe1938e82e-MathJax-1020-QINU 。
これを用いて、モーメントを書きなおすと、
UNIQ473e03fe1938e82e-MathJax-1021-QINU
となる。
これは、質点系の重心の位置に質点系の全質量が集中している時の、
原点周りの重力のモーメントに等しい。
回転運動の方程式
UNIQ473e03fe1938e82e-MathJax-1022-QINU が、あらゆる回転軸にかんする回転力を表現していることがわかった。
力UNIQ473e03fe1938e82e-MathJax-1023-QINUと運動量の変化の関係をあたえるニュートンの運動方程式（第2法則）を変形して、
回転力UNIQ473e03fe1938e82e-MathJax-1024-QINUにかんする方程式を導こう。
直交右手座標系UNIQ473e03fe1938e82e-MathJax-1025-QINU を定める。原点 UNIQ473e03fe1938e82e-MathJax-1026-QINU は、考察対象に都合のよい点を選ぶ。
剛体をUNIQ473e03fe1938e82e-MathJax-1027-QINU個の（質点と考えてよい）微小部分UNIQ473e03fe1938e82e-MathJax-1028-QINUに分け、
その質量をUNIQ473e03fe1938e82e-MathJax-1029-QINU、位置ベクトルをUNIQ473e03fe1938e82e-MathJax-1030-QINUとする。
UNIQ473e03fe1938e82e-MathJax-1031-QINUが外部から受ける力をUNIQ473e03fe1938e82e-MathJax-1032-QINU、
UNIQ473e03fe1938e82e-MathJax-1033-QINU が剛体の他の部分UNIQ473e03fe1938e82e-MathJax-1034-QINU から受ける力(内力)をUNIQ473e03fe1938e82e-MathJax-1035-QINUとおく。
後者は、剛体が変形しないよう、剛体の原子間に働かせる力に起因する。
この原子間の力は、原子の電荷による電気力と、
原子同士が接近しすぎたときに作用する量子力学的力により生じる。
作用・反作用の法則（運動の第3法則）から、UNIQ473e03fe1938e82e-MathJax-1036-QINU 。
さらに、剛体の２点間に働く内力の方向は、
その２点を結ぶ直線の方向と同じだと、仮定する。
各質点のニュートンの運動方程式
各質点ごとに、ニュートンの運動方程式を立てると、
UNIQ473e03fe1938e82e-MathJax-1037-QINU
これを変形して
UNIQ473e03fe1938e82e-MathJax-1038-QINU UNIQ473e03fe1938e82e-MathJax-1039-QINU
この式から、
力UNIQ473e03fe1938e82e-MathJax-1040-QINUの回転力UNIQ473e03fe1938e82e-MathJax-1041-QINUにかんする式を導こう。
UNIQ473e03fe1938e82e-MathJax-1042-QINUにかんする式の誘導
式（１）の両辺に左側から、UNIQ473e03fe1938e82e-MathJax-1043-QINU のベクトル積を施すと、
UNIQ473e03fe1938e82e-MathJax-1044-QINU UNIQ473e03fe1938e82e-MathJax-1045-QINU
ベクトル積の性質３と性質４により、
UNIQ473e03fe1938e82e-MathJax-1046-QINU UNIQ473e03fe1938e82e-MathJax-1047-QINU
ここで、ベクトル積の性質８より
UNIQ473e03fe1938e82e-MathJax-1048-QINU
なので、
UNIQ473e03fe1938e82e-MathJax-1049-QINU
質点UNIQ473e03fe1938e82e-MathJax-1050-QINUの運動量をUNIQ473e03fe1938e82e-MathJax-1051-QINUと書くと、
UNIQ473e03fe1938e82e-MathJax-1052-QINUなので、
UNIQ473e03fe1938e82e-MathJax-1053-QINU
定義；角運動量(運動量のモーメントともいう）
質点の位置ベクトルをUNIQ473e03fe1938e82e-MathJax-1054-QINU、運動量をUNIQ473e03fe1938e82e-MathJax-1055-QINUと書くとき、
UNIQ473e03fe1938e82e-MathJax-1056-QINUを,この質点の角運動量と呼ぶ。
これを用いると、
UNIQ473e03fe1938e82e-MathJax-1057-QINU
回転の運動方程式の導出
故に、
UNIQ473e03fe1938e82e-MathJax-1058-QINU
ここで、
UNIQ473e03fe1938e82e-MathJax-1059-QINU
式（４）の右辺の第２項の上付き添え字i,jを、それぞれ、j'と i'でおきかえられるので、
UNIQ473e03fe1938e82e-MathJax-1060-QINU
内力は作用反作用の法則が適用できると仮定しているので、
UNIQ473e03fe1938e82e-MathJax-1061-QINU 。この式を上の式の右辺に代入すると、
UNIQ473e03fe1938e82e-MathJax-1062-QINU
この式の右辺の和をとる変数i',j' を i,j におきかえると、
UNIQ473e03fe1938e82e-MathJax-1063-QINU
この式を、式（5）の右辺の第２項に代入して整頓すると、
UNIQ473e03fe1938e82e-MathJax-1064-QINU
さらに、内力に関する第２の仮定により、UNIQ473e03fe1938e82e-MathJax-1065-QINU とUNIQ473e03fe1938e82e-MathJax-1066-QINUは同じ方向なので、ベクトル積の定義より、この項は、零となることが分かる。
故に、式（４）の右辺の第２項は零となり、
UNIQ473e03fe1938e82e-MathJax-1067-QINU
が得られる。全角運動量をUNIQ473e03fe1938e82e-MathJax-1068-QINUとおけば、
式（６）は、次のように書ける。
命題；回転運動の関するオイラーの運動方程式
剛体の内力に上述の2つの仮定を付ける。このとき、
剛体に作用する全ての外部力の原点周りの力のモーメントUNIQ473e03fe1938e82e-MathJax-1069-QINUと、
全角運動量UNIQ473e03fe1938e82e-MathJax-1070-QINUの間には、
UNIQ473e03fe1938e82e-MathJax-1071-QINU （７）
この命題の導出までは詳しく述べたが、本テキストではこれ以上は深入りしない。
この先にも興味がある方は、次の記事をご覧ください。
固定軸の周りの剛体の回転運動の方程式
回転運動の運動方程式から、任意の軸の周りの回転運動の方程式が簡単に導出できる。
ｚ軸周りの場合を例にとり、説明する。
ｚ軸周りの回転力はUNIQ473e03fe1938e82e-MathJax-1072-QINUなので、
回転運動の方程式から
UNIQ473e03fe1938e82e-MathJax-1073-QINU
この式の右辺に,UNIQ473e03fe1938e82e-MathJax-1074-QINU を代入すると
右辺
UNIQ473e03fe1938e82e-MathJax-1075-QINU 微分の加法性から
UNIQ473e03fe1938e82e-MathJax-1076-QINU 内積の加法性から
UNIQ473e03fe1938e82e-MathJax-1077-QINU ベクトル積の性質８から
UNIQ473e03fe1938e82e-MathJax-1078-QINU UNIQ473e03fe1938e82e-MathJax-1079-QINUを代入し、ベクトル積の性質を用いると、
UNIQ473e03fe1938e82e-MathJax-1080-QINU
故に、
UNIQ473e03fe1938e82e-MathJax-1081-QINU
剛体はｚ軸の周りを回転するので、
その各点UNIQ473e03fe1938e82e-MathJax-1082-QINU(位置ベクトルUNIQ473e03fe1938e82e-MathJax-1083-QINU）は、
ｚ軸と直交する平面上を、ｚ軸を中心とする円を描いて運動する。
この拘束条件を考慮して、
時刻UNIQ473e03fe1938e82e-MathJax-1084-QINUの位置ベクトルUNIQ473e03fe1938e82e-MathJax-1085-QINUの座標成分を書きなおすと、
UNIQ473e03fe1938e82e-MathJax-1086-QINU
ここでUNIQ473e03fe1938e82e-MathJax-1087-QINUは、点UNIQ473e03fe1938e82e-MathJax-1088-QINUとｚ軸との距離、
UNIQ473e03fe1938e82e-MathJax-1089-QINUは、UNIQ473e03fe1938e82e-MathJax-1090-QINUをｘｙ平面に正射影した像がｘ軸となす角度である。図参照。
剛体につけておいた印UNIQ473e03fe1938e82e-MathJax-1091-QINUの位置ベクトルUNIQ473e03fe1938e82e-MathJax-1092-QINUを
ｘｙ平面に正射影した像がｘ軸となす角（回転角）UNIQ473e03fe1938e82e-MathJax-1093-QINUを用いると、
UNIQ473e03fe1938e82e-MathJax-1094-QINU
（UNIQ473e03fe1938e82e-MathJax-1095-QINUは、UNIQ473e03fe1938e82e-MathJax-1096-QINUごとに決まる、定数）と書ける。
式（１）の右辺を、式（２）を利用して、変形すると、
UNIQ473e03fe1938e82e-MathJax-1097-QINU
UNIQ473e03fe1938e82e-MathJax-1098-QINU
ベクトル積の性質６より、
UNIQ473e03fe1938e82e-MathJax-1099-QINU
UNIQ473e03fe1938e82e-MathJax-1100-QINU
UNIQ473e03fe1938e82e-MathJax-1101-QINU
ここで、UNIQ473e03fe1938e82e-MathJax-1102-QINUを代入すると
UNIQ473e03fe1938e82e-MathJax-1103-QINU
以上により、
UNIQ473e03fe1938e82e-MathJax-1104-QINU
UNIQ473e03fe1938e82e-MathJax-1105-QINU
が得られた。
UNIQ473e03fe1938e82e-MathJax-1106-QINUとおくと、この式は
UNIQ473e03fe1938e82e-MathJax-1107-QINU
と書ける。ここでUNIQ473e03fe1938e82e-MathJax-1108-QINUを、剛体の軸まわりの慣性モーメントと呼ぶ。
これがｚ軸を固定軸とする剛体の回転運動の運動方程式である。
原点を始点とする任意の回転軸UNIQ473e03fe1938e82e-MathJax-1109-QINUまわりの回転の方程式も同様に得られる。
この方程式の変数UNIQ473e03fe1938e82e-MathJax-1110-QINU は、一次元のスカラーなので、
質点がなめらかに拘束され、直線上を運動するときの運動方程式
UNIQ473e03fe1938e82e-MathJax-1111-QINU
と、対比させる。すると、
質点に作用する力 UNIQ473e03fe1938e82e-MathJax-1112-QINU ＜＝＝＝＞ 剛体に作用する回転力UNIQ473e03fe1938e82e-MathJax-1113-QINU
質点の質量 UNIQ473e03fe1938e82e-MathJax-1114-QINU ＜＝＝＝＞ 剛体のUNIQ473e03fe1938e82e-MathJax-1115-QINU軸まわりの慣性モーメント
UNIQ473e03fe1938e82e-MathJax-1116-QINU、UNIQ473e03fe1938e82e-MathJax-1117-QINUは質量UNIQ473e03fe1938e82e-MathJax-1118-QINUとUNIQ473e03fe1938e82e-MathJax-1119-QINU軸を延長した直線との距離
質点の位置変数 UNIQ473e03fe1938e82e-MathJax-1120-QINU ＜＝＝＝＞ 剛体のUNIQ473e03fe1938e82e-MathJax-1121-QINU軸周りの回転角変数UNIQ473e03fe1938e82e-MathJax-1122-QINU
質点の速度 UNIQ473e03fe1938e82e-MathJax-1123-QINU ＜＝＝＝＞剛体のUNIQ473e03fe1938e82e-MathJax-1124-QINU軸周りの角速度UNIQ473e03fe1938e82e-MathJax-1125-QINU;
質点の運動量 UNIQ473e03fe1938e82e-MathJax-1126-QINU ＜＝＝＝＞ 剛体の角運動量UNIQ473e03fe1938e82e-MathJax-1127-QINU;
運動方程式UNIQ473e03fe1938e82e-MathJax-1128-QINU ＜＝＝＝＞ UNIQ473e03fe1938e82e-MathJax-1129-QINU
という、対応関係があることが分かる。
この節で得た固定軸まわりの回転運動の方程式から、
もしUNIQ473e03fe1938e82e-MathJax-1130-QINU ならば、任意の軸まわりの回転力が零なので、
剛体の任意の軸まわりの角加速度が零、角速度が一定となることが分かる。
剛体の回転の運動エネルギー
剛体の各微小部分(質量UNIQ473e03fe1938e82e-MathJax-1131-QINU）の速度を UNIQ473e03fe1938e82e-MathJax-1132-QINUと書くと、
その運動エネルギーは UNIQ473e03fe1938e82e-MathJax-1133-QINUなので、
剛体全体の運動エネルギーは、UNIQ473e03fe1938e82e-MathJax-1134-QINU
回転運動している各微小部分の速度は、UNIQ473e03fe1938e82e-MathJax-1135-QINUと書けるので、
UNIQ473e03fe1938e82e-MathJax-1136-QINU
物理振り子
剛体は、重心を通らない水平軸の周りで、重力の作用を受け振動する。
これを物理振り子、あるいは実体振り子という。
水平回転軸をｘ軸とし、鉛直上方をｚ軸の正方向とし、yz平面が剛体の重心を通る座標系を考え、
回転軸とこの平面の交点を原点UNIQ473e03fe1938e82e-MathJax-1137-QINU、重心をUNIQ473e03fe1938e82e-MathJax-1138-QINUと記す。図参照。
回転はなめらかで摩擦力は無視できるとする。
すると、回転軸から、この剛体が受ける力は、剛体をこの軸に支える作用を持つだけで、剛体の振動に何の影響も与えない。
そこで、剛体にかかる力は、重力だけと考えて良い。
重力の原点周りの力のモーメントUNIQ473e03fe1938e82e-MathJax-1139-QINUは、
剛体の重心UNIQ473e03fe1938e82e-MathJax-1140-QINUに、剛体の全質量UNIQ473e03fe1938e82e-MathJax-1141-QINUがあるとしたときの
重力の原点周りのモーメントに等しいことが分かっている。
故に、
UNIQ473e03fe1938e82e-MathJax-1142-QINU
ｘ軸まわりの力のモーメントは、
UNIQ473e03fe1938e82e-MathJax-1143-QINU
従って、回転の運動方程式は
UNIQ473e03fe1938e82e-MathJax-1144-QINU
ここでUNIQ473e03fe1938e82e-MathJax-1145-QINUは、軸まわりの、振り子の慣性質量。
剛体の慣性モーメントの計算(一次元の剛体)
剛体UNIQ473e03fe1938e82e-MathJax-1146-QINUは、ごく細く、まっすぐな棒で,
長さUNIQ473e03fe1938e82e-MathJax-1147-QINU、質量密度(単位長さあたりの質量)は一定でUNIQ473e03fe1938e82e-MathJax-1148-QINUとする。
棒の左端からUNIQ473e03fe1938e82e-MathJax-1149-QINUの場所UNIQ473e03fe1938e82e-MathJax-1150-QINUを通り、棒に直交する軸まわりの慣性モーメントを具体的に計算しよう。
UNIQ473e03fe1938e82e-MathJax-1151-QINUを原点とし、棒と同じ方向の数直線を考え、これを座標系として採用。
UNIQ473e03fe1938e82e-MathJax-1152-QINUと表現する。
剛体UNIQ473e03fe1938e82e-MathJax-1153-QINUの慣性モーメントは、
剛体を質点とみなせるほど細かい部分UNIQ473e03fe1938e82e-MathJax-1154-QINUに分割して、
各UNIQ473e03fe1938e82e-MathJax-1155-QINUの質量UNIQ473e03fe1938e82e-MathJax-1156-QINUと、UNIQ473e03fe1938e82e-MathJax-1157-QINUとUNIQ473e03fe1938e82e-MathJax-1158-QINUとの距離UNIQ473e03fe1938e82e-MathJax-1159-QINUを用いて、
UNIQ473e03fe1938e82e-MathJax-1160-QINUで定義した。但しUNIQ473e03fe1938e82e-MathJax-1161-QINU
剛体の分割と慣性モーメントの近似式・リーマン和
UNIQ473e03fe1938e82e-MathJax-1162-QINUの質量UNIQ473e03fe1938e82e-MathJax-1163-QINUは、UNIQ473e03fe1938e82e-MathJax-1164-QINUの長さUNIQ473e03fe1938e82e-MathJax-1165-QINUに質量密度UNIQ473e03fe1938e82e-MathJax-1166-QINUを掛ければ得られるので
UNIQ473e03fe1938e82e-MathJax-1167-QINUであり、
UNIQ473e03fe1938e82e-MathJax-1168-QINU
と書ける。
しかし、剛体UNIQ473e03fe1938e82e-MathJax-1169-QINUをいくら細かく分割しても、
各小区間UNIQ473e03fe1938e82e-MathJax-1170-QINUは大きさ(長さ)をもつので、
原点との距離UNIQ473e03fe1938e82e-MathJax-1171-QINUは、一つに定まらない。
そこで、各小区間UNIQ473e03fe1938e82e-MathJax-1172-QINUから、代表点UNIQ473e03fe1938e82e-MathJax-1173-QINUを選びだし、その点の原点からの距離UNIQ473e03fe1938e82e-MathJax-1174-QINU、(UNIQ473e03fe1938e82e-MathJax-1175-QINU絶対値)を、UNIQ473e03fe1938e82e-MathJax-1176-QINUとみなす。
すると、慣性モーメントUNIQ473e03fe1938e82e-MathJax-1177-QINUの式は
UNIQ473e03fe1938e82e-MathJax-1178-QINU
で近似される。
そこで、この分割を
UNIQ473e03fe1938e82e-MathJax-1179-QINU
と表し、
UNIQ473e03fe1938e82e-MathJax-1180-QINU
で,慣性モーメントの近似式を表すことにする。
すると、
慣性モーメントの近似式は、
UNIQ473e03fe1938e82e-MathJax-1181-QINU
と書ける。
この値は分割の仕方と分割小区間の代表点UNIQ473e03fe1938e82e-MathJax-1182-QINUの選び方によって変化する。
UNIQ473e03fe1938e82e-MathJax-1183-QINUの中で、原点に最も近い点UNIQ473e03fe1938e82e-MathJax-1184-QINUにとると
最小値
UNIQ473e03fe1938e82e-MathJax-1185-QINU
をとり、
UNIQ473e03fe1938e82e-MathJax-1186-QINUの中で、原点に最も遠い点UNIQ473e03fe1938e82e-MathJax-1187-QINUにとると
最大値 UNIQ473e03fe1938e82e-MathJax-1188-QINU
を取る。
関数UNIQ473e03fe1938e82e-MathJax-1189-QINUを使って表現すれば、
UNIQ473e03fe1938e82e-MathJax-1190-QINU
であり、UNIQ473e03fe1938e82e-MathJax-1191-QINUを満たす。
質量密度が場所で変わるときは、、関数はUNIQ473e03fe1938e82e-MathJax-1192-QINUになり、
剛体の重心を求めるときは、後述するように、別の関数が現れる。
そこで、数学の分野では、一般の関数UNIQ473e03fe1938e82e-MathJax-1193-QINUにたいして
UNIQ473e03fe1938e82e-MathJax-1194-QINU
を求め、分割UNIQ473e03fe1938e82e-MathJax-1195-QINUとUNIQ473e03fe1938e82e-MathJax-1196-QINUの代表点UNIQ473e03fe1938e82e-MathJax-1197-QINUに関する関数UNIQ473e03fe1938e82e-MathJax-1198-QINUのリーマン和と呼ぶ。
その最小値UNIQ473e03fe1938e82e-MathJax-1199-QINUと最大値UNIQ473e03fe1938e82e-MathJax-1200-QINUも,同様に定義される。
UNIQ473e03fe1938e82e-MathJax-1201-QINU
慣性モーメントの近似式(1)は、関数UNIQ473e03fe1938e82e-MathJax-1202-QINUにたいするリーマン和である。
慣性モーメントの近似式の意味
今後、関数UNIQ473e03fe1938e82e-MathJax-1203-QINUは、UNIQ473e03fe1938e82e-MathJax-1204-QINUで定義された有界関数として、
議論を進める。
有界関数とは、十分大きな正数UNIQ473e03fe1938e82e-MathJax-1205-QINUを選べば、
UNIQ473e03fe1938e82e-MathJax-1206-QINUの全ての点UNIQ473e03fe1938e82e-MathJax-1207-QINUに対して、UNIQ473e03fe1938e82e-MathJax-1208-QINUとなること。
UNIQ473e03fe1938e82e-MathJax-1209-QINUを代入すれば、考察対象の剛体の慣性モーメントの話になる。
リーマン和
UNIQ473e03fe1938e82e-MathJax-1210-QINU
は、UNIQ473e03fe1938e82e-MathJax-1211-QINUのグラフを、棒グラフで近似したときの棒グラフの作る面積(各角柱の面積和)であることが分かる。図参照。
また、UNIQ473e03fe1938e82e-MathJax-1212-QINUは一点鎖線でしめす、小さいほうの長方形の和であり、
UNIQ473e03fe1938e82e-MathJax-1213-QINUは点線でしめす、大きいほうの長方形の和である。
UNIQ473e03fe1938e82e-MathJax-1214-QINUは、UNIQ473e03fe1938e82e-MathJax-1215-QINUのグラフとｘ軸およびｙ軸と平行な直線UNIQ473e03fe1938e82e-MathJax-1216-QINU、UNIQ473e03fe1938e82e-MathJax-1217-QINUで囲まれる部分の面積UNIQ473e03fe1938e82e-MathJax-1218-QINUを近似している。
また、UNIQ473e03fe1938e82e-MathJax-1219-QINU
であり、
UNIQ473e03fe1938e82e-MathJax-1220-QINUは面積を下から評価し、
UNIQ473e03fe1938e82e-MathJax-1221-QINUは面積を上から評価していることがわかる。
分割を限りなく細かくしていくとき、
リーマン和が分割や代表点の選び方に関係ない数に収束するならば、
その極限値は、
UNIQ473e03fe1938e82e-MathJax-1222-QINUのグラフとｘ軸およびｙ軸と平行な直線UNIQ473e03fe1938e82e-MathJax-1223-QINU、UNIQ473e03fe1938e82e-MathJax-1224-QINUで囲まれる部分の面積
と考えられる。
もし、分割UNIQ473e03fe1938e82e-MathJax-1225-QINUを細かくしていくとき
UNIQ473e03fe1938e82e-MathJax-1226-QINUとUNIQ473e03fe1938e82e-MathJax-1227-QINUが同じ値に収束することが示せれば、
(3)式と(4)式から、リーマン和は、関数のグラフの作る面積UNIQ473e03fe1938e82e-MathJax-1228-QINUに収束することが分かった。
可積分の定義と積分
「分割を細かくしていくとき、リーマン和が収束する」ということは、
面積を決める上で決定的に重要がことなので、
可積分という名を付けて、数学的に厳密に定義する。
このためにはまず、分割の大きさを定める必要がある。
定義：分割の大きさ
分割 UNIQ473e03fe1938e82e-MathJax-1229-QINUの大きさとは、
UNIQ473e03fe1938e82e-MathJax-1230-QINU
定義：可積分と積分
UNIQ473e03fe1938e82e-MathJax-1231-QINUを、有界閉区間UNIQ473e03fe1938e82e-MathJax-1232-QINU上で定義され、実数の値をとる関数とする。
もし、ある実数UNIQ473e03fe1938e82e-MathJax-1233-QINUが存在して、
どんな分割UNIQ473e03fe1938e82e-MathJax-1234-QINUと代表点UNIQ473e03fe1938e82e-MathJax-1235-QINUであっても、
UNIQ473e03fe1938e82e-MathJax-1236-QINU
が成り立つ時、
UNIQ473e03fe1938e82e-MathJax-1237-QINUはUNIQ473e03fe1938e82e-MathJax-1238-QINU上で(リーマン)可積分であるという。
このとき、UNIQ473e03fe1938e82e-MathJax-1239-QINU をUNIQ473e03fe1938e82e-MathJax-1240-QINUのUNIQ473e03fe1938e82e-MathJax-1241-QINU上での(リーマン)積分といい、
UNIQ473e03fe1938e82e-MathJax-1242-QINU
などと書く。
積分の性質
定理（積分の線形性）
UNIQ473e03fe1938e82e-MathJax-1243-QINUを、区間UNIQ473e03fe1938e82e-MathJax-1244-QINU上で定義された、任意の実数値関数であり、
UNIQ473e03fe1938e82e-MathJax-1245-QINUを任意の実数とする。
このとき、
（１）UNIQ473e03fe1938e82e-MathJax-1246-QINUがUNIQ473e03fe1938e82e-MathJax-1247-QINU上で可積分ならば、UNIQ473e03fe1938e82e-MathJax-1248-QINUもUNIQ473e03fe1938e82e-MathJax-1249-QINU上で可積分
（２）このとき、UNIQ473e03fe1938e82e-MathJax-1250-QINU
証明；リーマン和の定義から、区間UNIQ473e03fe1938e82e-MathJax-1251-QINUの任意の分割UNIQ473e03fe1938e82e-MathJax-1252-QINUと
分割区間の任意の代表点UNIQ473e03fe1938e82e-MathJax-1253-QINU(UNIQ473e03fe1938e82e-MathJax-1254-QINUはUNIQ473e03fe1938e82e-MathJax-1255-QINUに含まれる意)に対して、
UNIQ473e03fe1938e82e-MathJax-1256-QINU
UNIQ473e03fe1938e82e-MathJax-1257-QINUは可積分なので、その定義から、
UNIQ473e03fe1938e82e-MathJax-1258-QINU
UNIQ473e03fe1938e82e-MathJax-1259-QINU
(1)式の両辺の極限UNIQ473e03fe1938e82e-MathJax-1260-QINU をとろう。
右辺の極限
UNIQ473e03fe1938e82e-MathJax-1261-QINU
極限の性質から、
UNIQ473e03fe1938e82e-MathJax-1262-QINU
UNIQ473e03fe1938e82e-MathJax-1263-QINU
従って（１）式の左辺の極限UNIQ473e03fe1938e82e-MathJax-1264-QINU も存在して、右辺の極限と一致する。
証明終わり。
慣性モーメントの計算（１）リーマン和の極限を求める方法
UNIQ473e03fe1938e82e-MathJax-1265-QINUは、先述の、ごく細い一様な質量密度UNIQ473e03fe1938e82e-MathJax-1266-QINUのまっすぐな棒で、
座標系を入れて、UNIQ473e03fe1938e82e-MathJax-1267-QINUと表現しておく。
原点を通りこの棒と直交する軸のまわりの(この棒の)慣性モーメントを、
リーマン和の極限を取って求めよう。
区間UNIQ473e03fe1938e82e-MathJax-1268-QINUをｎ(UNIQ473e03fe1938e82e-MathJax-1269-QINU)等分して得られる点列,
UNIQ473e03fe1938e82e-MathJax-1270-QINU
を分点とする分割をUNIQ473e03fe1938e82e-MathJax-1271-QINUと記す。すると、
UNIQ473e03fe1938e82e-MathJax-1272-QINU, UNIQ473e03fe1938e82e-MathJax-1273-QINUであり、
UNIQ473e03fe1938e82e-MathJax-1274-QINU
UNIQ473e03fe1938e82e-MathJax-1275-QINUという分割の列は、
UNIQ473e03fe1938e82e-MathJax-1276-QINUを満たす。
UNIQ473e03fe1938e82e-MathJax-1277-QINUがリーマン可積分であることを認めれば、
可積分の定義から、どんな代表点UNIQ473e03fe1938e82e-MathJax-1278-QINUを選んでも、
UNIQ473e03fe1938e82e-MathJax-1279-QINUとなる。
そこで、代表点をUNIQ473e03fe1938e82e-MathJax-1280-QINUと選ぶ。
関数UNIQ473e03fe1938e82e-MathJax-1281-QINUを用いると、
分割UNIQ473e03fe1938e82e-MathJax-1282-QINUを用いた慣性モーメントの近似値は次のようになる。
UNIQ473e03fe1938e82e-MathJax-1283-QINU
ここで、
UNIQ473e03fe1938e82e-MathJax-1284-QINU(注参照）を利用して、この式を計算すると、
UNIQ473e03fe1938e82e-MathJax-1285-QINU
UNIQ473e03fe1938e82e-MathJax-1286-QINUなので、
UNIQ473e03fe1938e82e-MathJax-1287-QINU
故に、
UNIQ473e03fe1938e82e-MathJax-1288-QINU
（注）UNIQ473e03fe1938e82e-MathJax-1289-QINUの証明
UNIQ473e03fe1938e82e-MathJax-1290-QINU なので、両辺のj=1,2,,,n に関する和を取る。
左辺の和はUNIQ473e03fe1938e82e-MathJax-1291-QINU
右辺の和はUNIQ473e03fe1938e82e-MathJax-1292-QINU
故に、UNIQ473e03fe1938e82e-MathJax-1293-QINU
UNIQ473e03fe1938e82e-MathJax-1294-QINU UNIQ473e03fe1938e82e-MathJax-1295-QINU
UNIQ473e03fe1938e82e-MathJax-1296-QINUの略証
UNIQ473e03fe1938e82e-MathJax-1297-QINUなので、この両辺のj=1,2,,,nに関する和を取る。
左辺の和はUNIQ473e03fe1938e82e-MathJax-1298-QINU、右辺の和はUNIQ473e03fe1938e82e-MathJax-1299-QINU,故にUNIQ473e03fe1938e82e-MathJax-1300-QINU
慣性モーメントの計算（2）原始関数を利用する方法
積分可能な関数の積分をリーマン和の極限から求める計算は煩雑であり、複雑な形状の剛体の慣性モーメントを求めるにはふさわしくない。
次の定理が強力な計算法を提供する。
定理
UNIQ473e03fe1938e82e-MathJax-1301-QINUを数直線上の区間、
UNIQ473e03fe1938e82e-MathJax-1302-QINUをUNIQ473e03fe1938e82e-MathJax-1303-QINU上可積分な実数値関数
とする。
もしUNIQ473e03fe1938e82e-MathJax-1304-QINUが、
UNIQ473e03fe1938e82e-MathJax-1305-QINU上で微分可能で
全てのUNIQ473e03fe1938e82e-MathJax-1306-QINUの点UNIQ473e03fe1938e82e-MathJax-1307-QINUで、UNIQ473e03fe1938e82e-MathJax-1308-QINU
を満たす関数ならば(注参照)、
UNIQ473e03fe1938e82e-MathJax-1309-QINU
上記の条件を満たす関数UNIQ473e03fe1938e82e-MathJax-1310-QINUを、UNIQ473e03fe1938e82e-MathJax-1311-QINUの原始関数という。
(注)関数UNIQ473e03fe1938e82e-MathJax-1312-QINUは、UNIQ473e03fe1938e82e-MathJax-1313-QINU上でしか定義されていないので、
端点UNIQ473e03fe1938e82e-MathJax-1314-QINUでは、通常の微分は定義できない。そこで、
UNIQ473e03fe1938e82e-MathJax-1315-QINU
UNIQ473e03fe1938e82e-MathJax-1316-QINU
と定義する。
証明；
区間UNIQ473e03fe1938e82e-MathJax-1317-QINUの任意の分割
UNIQ473e03fe1938e82e-MathJax-1318-QINU
に対して、
代表点をUNIQ473e03fe1938e82e-MathJax-1319-QINU(UNIQ473e03fe1938e82e-MathJax-1320-QINUはUNIQ473e03fe1938e82e-MathJax-1321-QINUの点の意)とすると、
UNIQ473e03fe1938e82e-MathJax-1322-QINUのリーマン和は
UNIQ473e03fe1938e82e-MathJax-1323-QINU
UNIQ473e03fe1938e82e-MathJax-1324-QINU
小区間UNIQ473e03fe1938e82e-MathJax-1325-QINUでの関数UNIQ473e03fe1938e82e-MathJax-1326-QINUの平均勾配
UNIQ473e03fe1938e82e-MathJax-1327-QINU
は、平均値の定理により、
UNIQ473e03fe1938e82e-MathJax-1328-QINUの中のある一点UNIQ473e03fe1938e82e-MathJax-1329-QINUにおけるUNIQ473e03fe1938e82e-MathJax-1330-QINUの接線の勾配
UNIQ473e03fe1938e82e-MathJax-1331-QINUに等しので、
UNIQ473e03fe1938e82e-MathJax-1332-QINU
故に、UNIQ473e03fe1938e82e-MathJax-1333-QINU
そこで、各小区間UNIQ473e03fe1938e82e-MathJax-1334-QINUの代表点をUNIQ473e03fe1938e82e-MathJax-1335-QINUと選べば、
UNIQ473e03fe1938e82e-MathJax-1336-QINU
UNIQ473e03fe1938e82e-MathJax-1337-QINU
UNIQ473e03fe1938e82e-MathJax-1338-QINU
UNIQ473e03fe1938e82e-MathJax-1339-QINU
UNIQ473e03fe1938e82e-MathJax-1340-QINUは可積分なので、
UNIQ473e03fe1938e82e-MathJax-1341-QINU
UNIQ473e03fe1938e82e-MathJax-1342-QINU
証明終わり。
さて、慣性モーメントを求めたい剛体では、
UNIQ473e03fe1938e82e-MathJax-1343-QINUなので、その原始関数は、
UNIQ473e03fe1938e82e-MathJax-1344-QINU
従って、慣性モーメントは、定理を適用して、
UNIQ473e03fe1938e82e-MathJax-1345-QINU
UNIQ473e03fe1938e82e-MathJax-1346-QINU,UNIQ473e03fe1938e82e-MathJax-1347-QINUを代入して、整頓すると、
UNIQ473e03fe1938e82e-MathJax-1348-QINU
重心の計算への応用
質量密度が場所により変わる、長さUNIQ473e03fe1938e82e-MathJax-1349-QINUのごく細い棒UNIQ473e03fe1938e82e-MathJax-1350-QINUの重心を求めてみよう。
考えやすくするため、
棒の一端を原点にし、他端がｘ軸の正の位置にくるように座標系UNIQ473e03fe1938e82e-MathJax-1351-QINUをいれる。
この座標系で剛体はUNIQ473e03fe1938e82e-MathJax-1352-QINUと書ける。
UNIQ473e03fe1938e82e-MathJax-1353-QINUを小区間UNIQ473e03fe1938e82e-MathJax-1354-QINUに分割（分割UNIQ473e03fe1938e82e-MathJax-1355-QINUと記す)し、これらの小区間を質点とみなせば、その重心は、
UNIQ473e03fe1938e82e-MathJax-1356-QINU
で定義された(1.1.1節参照)。ここでUNIQ473e03fe1938e82e-MathJax-1357-QINU は第ｉ質点の質量、UNIQ473e03fe1938e82e-MathJax-1358-QINU、
UNIQ473e03fe1938e82e-MathJax-1359-QINUは第ｉ質点の位置ベクトル。
ベクトルを座標成分表示すると、この問題では一次元なので、
UNIQ473e03fe1938e82e-MathJax-1360-QINU、UNIQ473e03fe1938e82e-MathJax-1361-QINU
しかし、実際には UNIQ473e03fe1938e82e-MathJax-1362-QINUは、質点ではないので、
位置ベクトルは、定まらない。
またその質量も密度が一定ならば、UNIQ473e03fe1938e82e-MathJax-1363-QINUできまるが、
密度が変化するならば、定まらない。
そこで、各小区間 UNIQ473e03fe1938e82e-MathJax-1364-QINUの代表点UNIQ473e03fe1938e82e-MathJax-1365-QINUを選び
UNIQ473e03fe1938e82e-MathJax-1366-QINU,UNIQ473e03fe1938e82e-MathJax-1367-QINU
で近似する。
すると分割UNIQ473e03fe1938e82e-MathJax-1368-QINUと代表点UNIQ473e03fe1938e82e-MathJax-1369-QINUに対応する、
質量UNIQ473e03fe1938e82e-MathJax-1370-QINUと重心UNIQ473e03fe1938e82e-MathJax-1371-QINUの近似値は、それぞれ
UNIQ473e03fe1938e82e-MathJax-1372-QINU
UNIQ473e03fe1938e82e-MathJax-1373-QINU
UNIQ473e03fe1938e82e-MathJax-1374-QINU
UNIQ473e03fe1938e82e-MathJax-1375-QINU
ここで、UNIQ473e03fe1938e82e-MathJax-1376-QINU
もし、関数UNIQ473e03fe1938e82e-MathJax-1377-QINUが積分可能ならば、分割UNIQ473e03fe1938e82e-MathJax-1378-QINUを細かくしていけば
UNIQ473e03fe1938e82e-MathJax-1379-QINU
UNIQ473e03fe1938e82e-MathJax-1380-QINU
もし関数UNIQ473e03fe1938e82e-MathJax-1381-QINUの原始関数UNIQ473e03fe1938e82e-MathJax-1382-QINUが存在する(UNIQ473e03fe1938e82e-MathJax-1383-QINU)ならば
UNIQ473e03fe1938e82e-MathJax-1384-QINU
もし関数UNIQ473e03fe1938e82e-MathJax-1385-QINUも積分可能ならば、分割UNIQ473e03fe1938e82e-MathJax-1386-QINUを細かくしていけば
UNIQ473e03fe1938e82e-MathJax-1387-QINU
UNIQ473e03fe1938e82e-MathJax-1388-QINU
もし関数UNIQ473e03fe1938e82e-MathJax-1389-QINUの原始関数UNIQ473e03fe1938e82e-MathJax-1390-QINUが存在する(UNIQ473e03fe1938e82e-MathJax-1391-QINU)ならば
UNIQ473e03fe1938e82e-MathJax-1392-QINU
例；UNIQ473e03fe1938e82e-MathJax-1393-QINUならば、UNIQ473e03fe1938e82e-MathJax-1394-QINUなので UNIQ473e03fe1938e82e-MathJax-1395-QINU
また、UNIQ473e03fe1938e82e-MathJax-1396-QINUとなるのでUNIQ473e03fe1938e82e-MathJax-1397-QINU
となり、UNIQ473e03fe1938e82e-MathJax-1398-QINU
例；UNIQ473e03fe1938e82e-MathJax-1399-QINUならば、UNIQ473e03fe1938e82e-MathJax-1400-QINUなので UNIQ473e03fe1938e82e-MathJax-1401-QINU
このときUNIQ473e03fe1938e82e-MathJax-1402-QINUなので
UNIQ473e03fe1938e82e-MathJax-1403-QINUである。UNIQ473e03fe1938e82e-MathJax-1404-QINU
２次元以上の物体の慣性モーメントについて
てこの原理と力のモーメント
図のように剛体の棒の中間に支点UNIQ473e03fe1938e82e-MathJax-1405-QINUがあり、
この点をとおり、図面に垂直な軸の周りを自由に回転する装置を梃子(てこ）と呼ぶ。
てこの原理
梃子の端UNIQ473e03fe1938e82e-MathJax-1406-QINUに力UNIQ473e03fe1938e82e-MathJax-1407-QINUが作用し、他端UNIQ473e03fe1938e82e-MathJax-1408-QINUに力UNIQ473e03fe1938e82e-MathJax-1409-QINUが作用して、
つりあう(静止し続ける)とき、２つの力の間にはどのような関係があるだろうか。
棒は軽くて無視できるとして考察する。
軸周りに静止し続けるということは、
固定軸まわりの運動方程式(1.4.3.5節)から、
梃子に働く外力UNIQ473e03fe1938e82e-MathJax-1410-QINUの、回転軸まわり回転力が零であることを意味する。
UNIQ473e03fe1938e82e-MathJax-1411-QINUを原点、回転軸をｚ軸,梃子の棒をｘ軸とする、直交座標系UNIQ473e03fe1938e82e-MathJax-1412-QINUを導入すると、
UNIQ473e03fe1938e82e-MathJax-1413-QINU
UNIQ473e03fe1938e82e-MathJax-1414-QINU
と表現できる。
そこで、1.4.3.2.3節(ｚ軸まわりの回転力の導出)から
ｚ軸まわりのトルク(回転力)は
UNIQ473e03fe1938e82e-MathJax-1415-QINU
となる。
従って
つりあい条件は、
UNIQ473e03fe1938e82e-MathJax-1416-QINU
これをてこの原理という。
UNIQ473e03fe1938e82e-MathJax-1417-QINU をUNIQ473e03fe1938e82e-MathJax-1418-QINUに比べて、非常に大きくとれば、
少しの力UNIQ473e03fe1938e82e-MathJax-1419-QINUで非常に大きな力UNIQ473e03fe1938e82e-MathJax-1420-QINUと釣り合わせることが出来ることが分かる。
てこの原理については、
も参照のこと。
剛体に働く力の作用線
力が作用する点を着力点といい、
着力点を通り力のベクトルと方向が等しい直線を、力の作用線という。
剛体に働く力は、その着力点をかえると、一般には、剛体の運動への効果が異なってしまう。
しかし、力のベクトル和と、力のモーメント和が不変となるように力の着力点を移動したり力の合成をすることは、
剛体の運動には全く影響がでないので、許される。
例えば、力の着力点をその作用線にそってうごかしたり、
同じ着力点をもつ複数の力を、それらのベクトル和に置き換えることは許される。。
剛体のつり合い
いくつかの力が作用し、剛体が静止したままであるか、
重心UNIQ473e03fe1938e82e-MathJax-1421-QINUが等速直線運動(静止も含む)を続け、
重心の周りの回転が変化しない(回転しないままか、同じ回転を続ける）場合に、
剛体（に作用している力）は釣り合っているという。
重心が等速直線運動を行うのは、
剛体に作用する外力のベクトル和が０になることであり、その場合に限る。
これについては、「1.1.1 質点系の運動と重心」で説明した。
重心周りの回転が変化しないのは、重心まわりの外力のモーメントの総和が０になることであり、この場合に限る。これについては、「1.2.3.5 固定軸の周りの剛体の回転運動の方程式」で説明した。
定理；剛体のつり合い
剛体に、外力UNIQ473e03fe1938e82e-MathJax-1422-QINUがはたらいている。
このとき、次の条件は同等である。
ⅰ）剛体は釣り合っている。
ⅱ）外力のベクトル和が零で、重心UNIQ473e03fe1938e82e-MathJax-1423-QINUまわりの外力のモーメントの和が零。
ⅲ）外力のベクトル和が零で、任意の固定点UNIQ473e03fe1938e82e-MathJax-1424-QINUまわりの外力のモーメントの和が零。
証明；条件ⅰ）とⅱ）が同等であることは、すでに、説明した。
条件ⅱ）とⅲ）の同等性を示そう。
外力の和が零であるという条件の下で、
「任意の固定点UNIQ473e03fe1938e82e-MathJax-1425-QINUまわりの外力のモーメントの和UNIQ473e03fe1938e82e-MathJax-1426-QINUは常に等しい」
ことを示せば良い。
外力UNIQ473e03fe1938e82e-MathJax-1427-QINUの作用点をUNIQ473e03fe1938e82e-MathJax-1428-QINUとする。
すると、
UNIQ473e03fe1938e82e-MathJax-1429-QINUまわりの外力のモーメントの和UNIQ473e03fe1938e82e-MathJax-1430-QINUは
UNIQ473e03fe1938e82e-MathJax-1431-QINU
任意の点UNIQ473e03fe1938e82e-MathJax-1432-QINUまわりの外力のモーメントの和UNIQ473e03fe1938e82e-MathJax-1433-QINUは
UNIQ473e03fe1938e82e-MathJax-1434-QINU
UNIQ473e03fe1938e82e-MathJax-1435-QINUを（１）式に代入すると
UNIQ473e03fe1938e82e-MathJax-1436-QINU
ベクトル積の性質から、
UNIQ473e03fe1938e82e-MathJax-1437-QINU
仮定と(2)式から、
UNIQ473e03fe1938e82e-MathJax-1438-QINU
故に、UNIQ473e03fe1938e82e-MathJax-1439-QINU
証明終わり。
気体と液体の圧力
この節では気体や液体を、
分子や原子という粒子から構成されるという微視的立場でなく、
巨視的に捉え空間的に滑らかな連続体であるとみなす。
連続体の内部の微小部分に働く力を考え、其の釣合いについて考え、
圧力の性質を導く。
気体や液体とは何か。
気体と液体の特徴
気体と液体は体積の変化には抵抗するが、
形の変化には、抵抗しない。(ただし非常に速い変化には抵抗する）。
但し、気体の体積変化への抵抗は小さく、液体は非常に大きい。
静止気体と液体の圧力
気体や液体は、その表面または内部に任意の面を考えると、その面で２分される部分は、
互いに他を押している。それらは大きさ・方向は等しく、逆向きである(作用反作用の法則)
単位面積当たりのこの力を応力とよぶ。
その発生は、重力の存在と前述の気体や液体の特徴(形の変化に抵抗しない)に起因する。
この力の性質を、気体・液体の特徴から導こう。
応力は面に垂直に働く
説明は便宜上、液体の語で述べる。
命題１：
静止した液体(気体)の表面あるいは内部に任意のなめらかな面(注参照)を考える。
この面上の応力は、常にこの面に直角に働く。
面と常に直角に働く応力を、圧力と呼ぶ。
(注)面のどの一点においても、その点にごく近い面の部分だけをみれば、平面とみなせる曲面のこと。
理由；
もし、ある面上のある一点UNIQ473e03fe1938e82e-MathJax-1440-QINUの周辺の微小面部分(Ｓと書く)で、押し合う力がこの面と平行な成分を持つとする。
Ｓは仮定より、平面（の一部）と考えてよい。
図のように、面部分Ｓとそれと平行な平面の一部Ｓ’から作られる、
非常に薄い液体の板状部分Ｖを考える。
するとＶがＳを通して液体から受ける力の総和UNIQ473e03fe1938e82e-MathJax-1441-QINUは、面Ｓと平行な成分をもつ。
面ＳとＳ’は、非常に近いので、
Ｓを挟んで押し合う力と、Ｓ’を挟んで押し合う力は、単位面積当たり、ほぼ等しいと考えてよい。
すると、ＶがＳ’を通して液体から受ける力UNIQ473e03fe1938e82e-MathJax-1442-QINUは、
Ｓを通して受ける力と大きさと方向はほぼ同じで、逆向きになる。
UNIQ473e03fe1938e82e-MathJax-1443-QINUの面Ｓと平行な成分も、UNIQ473e03fe1938e82e-MathJax-1444-QINUのＳと平行な成分と大きさはおなじで、逆向きになる。
液体は自由に形を変えられるので、ＶのＳ面とＳ’面は逆方向に動いてしまい、
静水という条件に反してしまう。
従って、
「ある面上のある一点UNIQ473e03fe1938e82e-MathJax-1445-QINUの周辺の微小面部分Ｓで、押し合う力がこの面と平行な成分を持つ」
という仮定はあり得ないことが示された。
命題２
どの面にも直角に働く応力(圧力)は、どの点でも面の方向によらず一定の強さ(大きさ)をもつ。
証明；
液体中の任意の点をUNIQ473e03fe1938e82e-MathJax-1446-QINUとする。
UNIQ473e03fe1938e82e-MathJax-1447-QINUを原点とする、直交右手系UNIQ473e03fe1938e82e-MathJax-1448-QINUを定める。
UNIQ473e03fe1938e82e-MathJax-1449-QINUを通る任意の面UNIQ473e03fe1938e82e-MathJax-1450-QINUをとる。
UNIQ473e03fe1938e82e-MathJax-1451-QINU点における、
この面における圧力UNIQ473e03fe1938e82e-MathJax-1452-QINUとｘｙ平面における圧力UNIQ473e03fe1938e82e-MathJax-1453-QINU、ｙｚ平面、ｚｘ平面における圧力UNIQ473e03fe1938e82e-MathJax-1454-QINU
が等しいことを示そう。
平面UNIQ473e03fe1938e82e-MathJax-1455-QINUと平行でUNIQ473e03fe1938e82e-MathJax-1456-QINU点の近くを通る平面UNIQ473e03fe1938e82e-MathJax-1457-QINUが
ｘ軸、ｙ軸、ｚ軸と交わる点をそれぞれ、
UNIQ473e03fe1938e82e-MathJax-1458-QINUとおく。図参照。
四面体UNIQ473e03fe1938e82e-MathJax-1459-QINUの外部の液体が、
UNIQ473e03fe1938e82e-MathJax-1460-QINUを押す力をUNIQ473e03fe1938e82e-MathJax-1461-QINU,UNIQ473e03fe1938e82e-MathJax-1462-QINUを押す力をUNIQ473e03fe1938e82e-MathJax-1463-QINU,UNIQ473e03fe1938e82e-MathJax-1464-QINUを押す力をUNIQ473e03fe1938e82e-MathJax-1465-QINU,UNIQ473e03fe1938e82e-MathJax-1466-QINUを押す力をUNIQ473e03fe1938e82e-MathJax-1467-QINU
とおく。
四面体内の液体が静止しているので、
UNIQ473e03fe1938e82e-MathJax-1468-QINU
が成り立つ。
この式を圧力で表示しよう。
UNIQ473e03fe1938e82e-MathJax-1469-QINUなので、
UNIQ473e03fe1938e82e-MathJax-1470-QINUが十分小さければ
UNIQ473e03fe1938e82e-MathJax-1471-QINU
故に、UNIQ473e03fe1938e82e-MathJax-1472-QINU
同様にUNIQ473e03fe1938e82e-MathJax-1473-QINU、
UNIQ473e03fe1938e82e-MathJax-1474-QINU
UNIQ473e03fe1938e82e-MathJax-1475-QINU
これらを(1)式に代入して
UNIQ473e03fe1938e82e-MathJax-1476-QINU
これを計算すると、
UNIQ473e03fe1938e82e-MathJax-1477-QINU
これより、UNIQ473e03fe1938e82e-MathJax-1478-QINU 証明終わり。
命題３
ⅰ）一様な重力のもとで静止している気体・液体内では、同一水平面上での圧力の大きさは一定である。
ⅱ）もし液体の密度UNIQ473e03fe1938e82e-MathJax-1479-QINUが圧力によって変化しないならば、
深さUNIQ473e03fe1938e82e-MathJax-1480-QINUの水平面UNIQ473e03fe1938e82e-MathJax-1481-QINU上の圧力UNIQ473e03fe1938e82e-MathJax-1482-QINUと
深さUNIQ473e03fe1938e82e-MathJax-1483-QINUの水平面UNIQ473e03fe1938e82e-MathJax-1484-QINU上の圧力UNIQ473e03fe1938e82e-MathJax-1485-QINUには
次の関係が成り立つ。
UNIQ473e03fe1938e82e-MathJax-1486-QINU
図示した液体部分UNIQ473e03fe1938e82e-MathJax-1487-QINUが静止しているので、UNIQ473e03fe1938e82e-MathJax-1488-QINUに作用する力の総和が零になっている。
このことから、この命題は容易に証明できる。
命題４ アルキメデスの原理
気体の圧力と大気圧
気体は圧力が増すと縮むので、命題３のⅱ）の結論は成立しない。
大気は静止していると仮定し、地表の大気圧から高度ｚでの大気圧を求めてみよう。
地表の一点を原点とし、鉛直上方をｚ軸の正方向になる座標UNIQ473e03fe1938e82e-MathJax-1489-QINUをいれる。
図のように、下底面が高さUNIQ473e03fe1938e82e-MathJax-1490-QINU、上底面が高さUNIQ473e03fe1938e82e-MathJax-1491-QINUの、単位断面積の角柱UNIQ473e03fe1938e82e-MathJax-1492-QINUを考える。
その部分の気体が受ける力の和は零となるので、
次式が成り立つ。
UNIQ473e03fe1938e82e-MathJax-1493-QINU
ここで
・UNIQ473e03fe1938e82e-MathJax-1494-QINUは高さUNIQ473e03fe1938e82e-MathJax-1495-QINUの地点の大気圧(命題３のⅰ）から、高度が同じ水平面上で圧力は一定）、
・UNIQ473e03fe1938e82e-MathJax-1496-QINUはUNIQ473e03fe1938e82e-MathJax-1497-QINUの質量。UNIQ473e03fe1938e82e-MathJax-1498-QINUの体積UNIQ473e03fe1938e82e-MathJax-1499-QINUと平均質量密度UNIQ473e03fe1938e82e-MathJax-1500-QINUの積。
圧力が大きいと空気は縮み質量密度は高くなるので、両者の関係を求めねばならない。
空気体積の変動にともなう温度変化がないとすると、
ボイルの法則(３章１節 熱とエネルギー参照)から、
UNIQ473e03fe1938e82e-MathJax-1501-QINU（UNIQ473e03fe1938e82e-MathJax-1502-QINUは温度だけに依存する数）
質量密度UNIQ473e03fe1938e82e-MathJax-1503-QINUを代入すると、
UNIQ473e03fe1938e82e-MathJax-1504-QINU,ゆえに、UNIQ473e03fe1938e82e-MathJax-1505-QINU
UNIQ473e03fe1938e82e-MathJax-1506-QINUを、UNIQ473e03fe1938e82e-MathJax-1507-QINUとおくと、
UNIQ473e03fe1938e82e-MathJax-1508-QINU
この質量密度と圧力の関係を用いると、
UNIQ473e03fe1938e82e-MathJax-1509-QINU（ｈが小さいほど差は少なくなる）
この式を(１)式に代入して、
UNIQ473e03fe1938e82e-MathJax-1510-QINU、変形すると
UNIQ473e03fe1938e82e-MathJax-1511-QINU。これより
UNIQ473e03fe1938e82e-MathJax-1512-QINU
を得る。これを積分して
UNIQ473e03fe1938e82e-MathJax-1513-QINU
を得る。
ここでUNIQ473e03fe1938e82e-MathJax-1514-QINUは、地表での圧力、UNIQ473e03fe1938e82e-MathJax-1515-QINUはネイピア数である。
地表での質量密度がUNIQ473e03fe1938e82e-MathJax-1516-QINUならば,(2)式から、
UNIQ473e03fe1938e82e-MathJax-1517-QINU
圧力の単位
圧力は、単位面積当たりの力なので、その単位は面積の単位UNIQ473e03fe1938e82e-MathJax-1518-QINUと力の単位UNIQ473e03fe1938e82e-MathJax-1519-QINUから得られる。
UNIQ473e03fe1938e82e-MathJax-1520-QINU
が圧力の単位で、パスカルと呼ばれる。
