物理/波の性質
提供: Internet Web School
目次 |
波の性質
波には色々あるが、この節では波に共通する性質を学ぶ。
参考文献;
波の次元
張った弦の振動のように、一次元空間を伝わる波を一次元の波、
水面のような2次元の空間を伝わる波を2次元の波、
空中や水中を伝わる音のように、3次元空間を伝わる波を3次元の波という。
波面と波面の形
波線・波面; 波の山をつないだ連続する図形や波の谷をつないだ連続図形のこと。
2次元の波では曲線になり波線という。
3次元の波では曲面になり波面という。
波面が平面になる3次元の波を平面波という。
また波面が球面になる3次元の波を球面波という。
2次元の波で、波線が直線になるものを2次元の平面波、波線が円になるものを2次元の球面波と便宜的に呼ぼう。
一様で、方向性のない3次元の媒体中の一点に方向性に無い変位を与え波を発生させると、
この点波源から全く同じ性質の波が、あらゆる方向に伝わっていくので、
波面は球面になる。
この球面波を波源から十分離れた場所で観測すると、
観測点の近くの限定された空間内では、平面波とみなせる。
波の進行方向 と速度
ある時刻tにおける波面$W(t)$を、その微小時間 $\delta t(>0)$後に観測すると、
その位置を少し変えている。その波面を$W(t+\delta t)$ とかく。
時刻 t の波面の一点 P から、
この波面に直行する直線をひき、波面$W(t+\delta t)$ との交点を P' とすると、
P' は波面$W(t)$上の一点Pが進行した場所と考えられる。
波の PP'間における平均速度は、 $\frac{\vec{PP'}}{\delta t}$ である。
$\lim_{\delta t \to 0}$ をとると、波面の一点Pにおける、時刻tの波の瞬時速度が得られる。
波の発生の仕組みと連続波とパルス波、縦と横波
変位に対して、もとに戻ろうとする力が生じる物質(注)では、
ある場所にわずかな、変位が与えられると
元の位置に戻ろうとして振動を生じ(波源)
これが隣接する媒質に力を与えて隣接部に振動をおこし、
物質(媒質)全体に振動が伝わっていく。
これが波である。
連続波とパルス波
波源の振動の持続回数により、2種類の波がおこる。
波源が連続的に振動し続ける場合には、
波源から連続的に波が生み出され、媒質全体に伝わって行くので、
連続する波がが生じる。連続波という。
また波源が一回の振動で変位がなくなる場合には、
一つの山(ないし谷)の波が波源から放出され、媒質の中を伝わっていく。
パルス波という。
縦波と横波
媒質がどのような変形に対して復元力を持つかに応じて、異なった形の波動が生じる。
縦波
圧縮・膨張に対する復元力を持つ媒質では、波源が急激に変位すると、
その変位方向の2つの隣接部分の一方$A_1$は、圧縮され(密度が大きくなり)、圧力は上がる。
すると、$A_1$と隣接する波源の変位方向の部分$A_2$は
$A_1$部分の媒質からの圧力を受けて圧縮され、圧力をあげる。
このとき、$A_1$部分は膨張し、密度を下げる。
このメカニズムにより、密度の振動が伝搬していく。
他方、波源の変位により、膨張し密度を下げた側でも同じメカニズムで、媒質の粗密の振動が、波源の変位方向(向きは逆)に伝搬していく。
この波は、媒質の粗密(圧力)の振動が波の進行方向と平行なので、
縦波(longitudinal waves)という。
粗密波とも呼ばれる。
横波
媒質が、横ずれに対して復元力を持つ場合では、別のタイプの波が生じる。
この場合、波源となる媒質部分が移動したとき、
波源は、変位方向と直角(上下と表現する)の隣接部分を引きずる。
このため、波源の左右への振動により、
上下にある隣接部分もやや遅れて引きずられて
その位置を左右に振動させ、これが媒質の上下方向の全体に伝わっていく。
この波の進行方向(上下)と、媒質の振動方向(左右)は直交するので、
横波(transverse waves)という。
張った弦の振動が横波の例である。
気体や液体の内部では、横ずれに対して復元力がないため横波は発生しない。
横波でも縦波でもない波
横波でも縦波でもない波もある。後述する水面の波が、その例である。
弾性波
媒質の変位により生じる波を弾性波と呼ぶ。
弾性波を生じない物質
2章で述べたように、かたい固体を理想化して、全く変形しない固体を考えて、剛体と名付けた。
現実の固い物質を理想化した剛体は、
どんなに外力を加えても圧縮、変形が起こらないので、剛体の中には波は発生しない。
現実の物質は弾性波を生じる
現実の物質は圧力をかければ、
程度の差はあるが、圧縮し、元のもどろうとする力が発生するので、縦波はおこる。
弾性波でない波
光や電波は電磁波という波の一種だが、真空中でもこの波は発生する。
したがって、波の媒質はなく、弾性波ではない。
あえて言えば、電磁波では、真空という空間が媒質で、
空間の電気的なゆがみ(電場、磁場と呼ぶ。次章を参照のこと)の
振動が伝搬して起こると考えられる。
この歪みは電磁波の進行方向と直交する方向におこるため、電磁波は横波である。
次の記事も参考に。
波の例
身の回りには色々な波が良く見られる。
媒質が空気である波は音(あるいは音波)であり、縦波である。
媒質が水の場合は水面波や水中の音波となる。
水面波は、
水面を伝わる、さざ波や小さな波のことである。
この波は、水面の上昇や下降時に、水の表面張力や重力が復元力として働くため生じる。
ところが、ある場所の水面が上下振動しても、
その鉛直下方にある水は殆ど膨張・圧縮されないので、
水面上昇時には隣接する水面下の水が流れ込み、下降時には、鉛直下方の水が隣接する水面の下方に押し出され、
波の進行方向する方向と平行の振動が起こる。
こうして水の表面部分は波が通過するとき、上下の振動に、
波の進行方向と平行な振動を合成した、円形の振動をする。
従って、縦波でも横波でもない。
固体は曲げやずれに対する復元力を持つので横波を起こすが、
わずかとはいえ、圧縮・膨張して、強い復元力を生じるため、縦波も起こす。
例えば、地震波は地殻の波だが
最初に到達するP波は縦波で、
遅れて到達するS波は横波である。
地表へは、地震波は下方から到達するので、縦波のP波は上下動、横波のS波は横揺れになる。
波形の数式による表示
まず、
波がなく平衡状態にある媒質が静止してみえる慣性系を選び、
時刻原点は考察に都合のよいものを選択する。
この座標系で表示した場所xと時間tにおける媒質の変位量を数式で表示すればよい。
波を数式表示すると、数学を利用して、波の色々な性質を知ることができる。
変位量について
波の変位量 $y(x,t)$ としては、幾つかのものが考えられ、どれを選択するかは、なかなか難しい問題である。
縦波では、
・時刻tにおける場所xでの、媒質の密度や圧力の平衡状態からの変化量を変位量とする。
・平衡状態でxにあった媒質の時刻tにおける位置の変化量を、変位量に取る。
また、媒質の位置そのものでなく、
場所xの時刻tでの媒質の速度を変位量としてとる。
等々。
横波では、
・波がないとき位置座標xにあった媒質が時刻tでいくら変位したかを変位量とする。
・光を含む電磁波は、真空を媒質とする横波で、場所xと時刻tでの、波の進行方向とは垂直な空間の電気的な歪み(3次元ベクトル)が、変位量になる。次章で述べる。
等々。
波の性質を調べるとき、何を変位量として選ぶかに依存する概念(例えば反射における自由端や固定端)があるので、変位量に注意する必要がある(後述)。
(注)気体や液体(流体と総称する)の縦波における媒質の位置変化量について;
平衡状態で、座標xの場所にある流体が、
波の到来でその位置をどのように変えるか決定することは、ミクロ(微視的)には出来ない。
なぜならば、
座標 $\vec x$ の場所にある流体や固体とは、その点にある分子ではなく
、
(マクロな観測では一点とみなせる)座標xを中心とする微小体積の中にある膨大な数の流体や固体分子全体をさす。
固体の場合には、これらの分子たちは、
それぞれが決まった位置の周りを熱運動等で振動するだけで塊を形成している。
波がきてもこの塊が塊を保ったまま動くだけなので、
マクロな観測では、波が到来しても、点 $\vec x$ にあた媒質が点として移動するように見える。
この場合には、波の変位量として、位置変化量を採用できる。
しかし、流体の場合、ある時点で、xの周辺にいる分子たちは
波が来ない平衡状態でも、熱運動のためやがて拡散して
ばらばらに四散してしまう。
水中にインクを静かに垂らしてもやがて拡散してしまうように。
しかし、マクロ(巨視的)には、波が来た瞬間のごく短時間には、まだ塊の状態で動くとみなして、位置変化を変位量とすることができる。
一次元波動の波形の数式表示
3次元の波では、
その波形は、独立変数が4つ(3次元空間の場所と時間)で、数式の扱いは難しくなり、
図示は不可能である。
一次元の波では、その波形の数式表示は簡潔である。
しかし、その応用範囲は広い。
たとえば、
張った弦や糸の振動などは一次元の横波である。
また、3次元空間の平面波も進行方向をx軸にえらべば、
この軸の上を伝わる一次元波動とみなせる。
同様に球面波は、波源からあらゆる方向に
速度も振動の仕方も全く同じ一次元波が放射されるので、
ひとつの一次元波を解析すればよい。
初期時刻の波形の表示
時刻の原点(初期時刻)を考察しやすいように選ぶ。
波の進行方向をx軸の正方向にとる。
波の変位量(縦波では媒質の圧力や巨視的な位置の変位量、横波では、媒質の巨視的な位置の変化量)をy軸にとる。
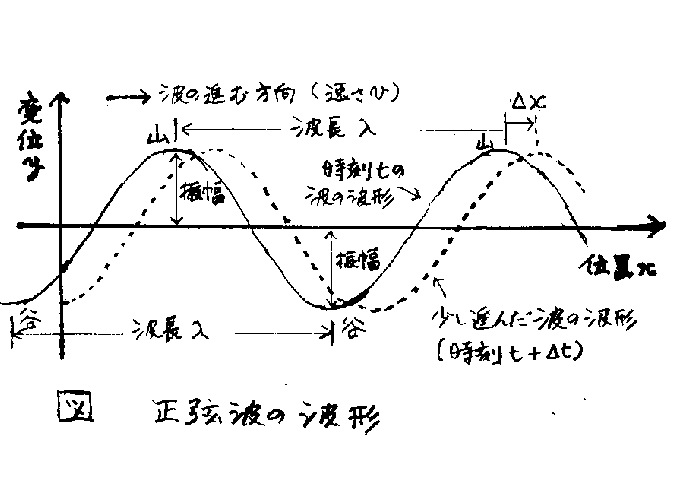
一例として、後述する正弦波の波形を図示する。
実線は時刻tでの波形、
点線は、その微小時間後の時刻$t+\Delta t$の波形である。
波は、x軸の正方向に進行している。
一般の波の初期時刻における波形が
$y=f(x)\qquad \qquad (1)$
と数式表示されるとする。
時刻tの波形の表示
式(1)で与えられる波がx軸上を速度 $v$ で進行しているとき(注参照)、
任意の時刻tの波形はどのように表示されるだろうか。
命題4.1
時刻0の波形を、
$y=f(x)\qquad \qquad (2)$
とする。
この波が、x軸上を速度 $v$ で進行するとき、
その波は、
$y=f(x-vt)$
で表せる。
証明;
任意の時刻tの波形を $y=g(x,t)$ とかく。
この波形は、式(2)の波形をx軸に沿って $vt$ 平行移動したものであるから、
式(2)の波形のxでの変位量$f(x)$は、
時刻tの波形では、 $x+vt$ の位置になっている。
数式で書くと
$f(x)=g(x+vt,t)$
$x$ に $x-vt$ を代入すると
$y=g(x,t)=f(x-vt)\qquad \qquad (3)$
これが、速度vでx軸の正方向に進む1次元の波の一般形である。
(注)vが負の時は、x軸の負の方向に進む。
単振動と正弦波
媒質の振動のうちもっとも基本的なものは、
正弦関数にしたがって振動する単振動である。
媒質の任意の一点を固定し、その点の時刻tの変位yが正弦関数
$y=A\sin(\omega t+\theta)\qquad (\omega \neq 0)\qquad \qquad (4)$
で表せるとき、この点は、単振動を行うという。
2章の力学で、フックの法則(注参照)を満たす「ばね」につながれた
おもりの運動は単振動することを学んだ。
ウィキペディア(自由振動) の 1 単振動 参照。
媒質の復元力がフックの法則を満たすならば、
外力を受けて変位した場所は単振動を起こし、この単振動が媒質全体に伝搬していく。
(注)フックの法則;復元力は変位量に正比例するという経験則。
単振動の振動数、周期と角速度
式(4)中の
$\quad$ $A$ は、変位の絶対値の最大値を表すので、振幅(amplitude)、
$\quad$ $\omega t+\theta$ は、振動の位置を表す角で、位相(phase)あるいは位相角,
$\quad $ $\omega$ は単位時間あたりの位相角の変化量をあらわすので、角速度(angular velocity)
$\quad$ $|\omega|$ は、角振動数
と呼ばれる。
定義
$T:=\frac{2\pi}{|\omega|} \qquad \qquad (5)$
を、式(4)で表される単振動の周期という。
$\nu=\frac{|\omega|}{2\pi} \qquad \qquad (6)$
を、単振動の振動数という。
この定義から、次の命題は明らかである。
命題4.2
$T=\frac{1}{\nu} \quad \nu=\frac{1}{T} \qquad \qquad (7)$
周期と振動数の意味
任意の時刻tから時間がT経過して、時刻t+Tになるとき、
位相角が $\omega T=\omega \frac{2\pi}{|\omega|} =\pm 2\pi$ だけ進むので、
ちょうど一回振動して元の変位に戻っている。
周期Tは波が一回振動して元に戻るまでの時間(>0)である。
また、振動数は、振動運動が単位時間当たりに繰り返される回数(>0)であることが分かる。
正弦波
波形が正弦関数であらわせる連続波を正弦波という。
媒質の復元力がフックの法則に従うならば、波源の振動も、それが伝搬した波に振動も、三角関数に従うため、正弦波が生じる。
また、復元力がフックの法則を満たさない場合でも、
変位量が小さい、振幅の小さい波では、復元力はほぼフックの法則に従うので、正弦波にちかい波が生じる。
そのため、正弦波は最も基本的な波といえる。
振幅が $A(\gt 0)$ の正弦波の初期時刻 t=0 の波形は,一般に
$y=f(x)=A\sin (kx+\theta) \qquad \qquad (8)$
と書ける。
ここで、$\theta$ は、初期時刻t=0の原点x=0での変位の位相であり、
初期位相という。
k は正、負両方になりえるので波数ベクトル(wave number vector),省略して波数という。(注参照)
隣り合う山の距離(隣り合う、等位相の点の距離)を、波長と呼ぶ。
式(8)で波形が表される波はx が $\pm \frac{2\pi}{|k|}$ だけ変わると同じ値(等位相)になるので、
波長は $\lambda=\frac{2\pi}{|k|}$
この波がx軸上を速度vで進むとき、その波は、命題4.1により
$y=f(x-vt)=A\sin \left(k(x-vt)+\theta\right)
=A\sin \left(kx-kvt+\theta\right)\qquad \qquad (9)$
ここで、
$\omega:=kv\qquad \qquad (10)$
と置くと、
$y=f(x-vt)=A\sin \left(kx-\omega t+\theta\right)\qquad \qquad (11)$
命題4.3
1次元の正弦波の波形が、
x軸上を $v=\frac{\omega}{k}$ の速度で進むならば
$y=A\sin \left(kx-\omega t+\theta\right)\qquad \qquad (12)$
と表せる。
ここで、
$\quad $ $A(\gt 0)$ は波の振幅、
$\quad $ $k$ は波の波数(ベクトル)、
$\quad $ $\omega$ は,波の角速度
$\quad $ $\theta$ は,波の初期位相
である。
(証明)
波の速度$v$ とおくと、波数kの波は、式(9)より、
$y=A\sin \left(k(x-vt)+\theta\right)
=A\sin \left(kx-kvt+\theta\right)\qquad \qquad $
と書ける。
$v=\frac{\omega}{k}$ を代入すれば、式(12)が得られる。
証明終わり。
周期的な波の波長、振動数、周期、速度の関係
命題4.4
正弦波の
波長を$\lambda$、波数をk、周期を $T$ 、振動数を $\nu$、角速度を $\omega$ とかくと、次の関係が成立つ。
(1) $T=\frac{1}{\nu},\quad \nu=\frac{1}{T},\quad T=\frac{2\pi}{|\omega|},\quad \nu=\frac{|\omega|}{2\pi},\quad |\omega|=2\pi \nu $
(2) $\lambda=\frac{2\pi}{|k|}\quad $
(3) $v=\frac{\omega}{k}$、$|v|=\lambda \nu$
証明;
(1) 一秒間に $\nu$ 回振動すれば、一回の振動にかかる時間(T)は $\frac{1}{\nu}$。
これより、最初の2つの等式が成立つ。
一回の振動に要する時間T(>0)は、位相角が $\pm 2\pi$ 変わる時間でもあるので、
$T=\frac{2\pi}{|\omega|}$。
一秒間に $\nu$ 回振動する波は、その間に位相角が $2\pi \nu $ 進むので、
$\omega=2\pi \nu $
(2) 波数がkである正弦波は、一般に次の式(13)で記述できる。
$y=A\sin (kx-\omega t+\theta)\qquad \qquad (13)$
波を波長 $\lambda$だけ、x軸に沿って移動させても、波形は一致するので、
$A\sin (kx-\omega t+\theta)=A\sin \left( k(x+\lambda)-\omega t+\theta \right) $
これより、$|k|\lambda $ は、$2\pi$ の整数(n)倍。
波長より短い距離を移動させても、波形は一致しないので、 $n=1$ 。
ゆえに、$|k|\lambda =2\pi$
(3) $y=A\sin (kx-\omega t+\theta)=A\sin \left(k(x-\frac{\omega}{k}t)+\theta\right)$
この波の位相角が $\theta$ である位置xは、
時間とともに $x=\frac{\omega}{k}t$に従って動く。
これより、波の速度は $v=\frac{\omega}{k}$ 。
$|v|=\frac{|\omega|}{|k|}=\frac{|omega|}{2\pi}\frac{2\pi}{|k|}$
$\quad$ (1)と(2)で示した等式から、
$\quad$ $=\nu \lambda$
(注)この命題で得られた関係から、
波数kと角速度 $\omega$ の符号を同時に変えても、他の定数は全く変化はない。
従って、波数kは正負どちらを選んでもよいことが分かる。
それに合わせて$\omega$の符号を選び、初期位相角を変えればよい。
通常は、波数kは正に選ぶ。
このことは、
正弦関数が$ \sin(x)=\sin(-x \pm \pi)$ を満たすことから、直接導ける
実際、
$\sin\left(k(x-\frac{\omega}{k}t)+\theta \right)
=\sin\left(-k(x-\frac{-\omega}{-k}t)-\theta \pm \pi \right) $
系;
正弦波は、命題4.4の関係を利用すると、次のように色々な表現ができる。
(1)$y=A\sin \left(k(x-vt)+\theta\right)\qquad \qquad (9)$
(2)$y=A\sin \left(\omega (\frac{x}{v}-t)+\theta\right)$
(3)$y=A\sin \left(2\pi \nu (t-\frac{x}{v})+{\theta}'\right)$
$\qquad$ ここで、${\theta}'$ は適切に選んだ初期位相角。
命題4.5
任意の場所xで、正弦波を観測すると、
単振動を行う。
証明;
命題4から、正弦波は
$y=A\sin \left(\frac{2\pi}{\lambda}(x-vt)+\theta\right) $
で表される。
この式で、xを固定し、tの関数 $h(t)$ としてみると
$y=h(t)=A\sin \left(-v\frac{2\pi}{\lambda}t+(\frac{2\pi}{\lambda}x+\theta)\right) $
この式で、$-v\frac{2\pi}{\lambda}$ を $k$で、
$\frac{2\pi}{\lambda}x+\theta$ を $\phi$ で表すと、
$y=h(t)=A\sin ((kt+\phi) $
であり、単振動であることが分かる。証明終わり。
波の波長と周波数の関係
波の速度の大きさが、媒質の性質だけで決まり、波長や振動数で変わらないので、
命題4.4 より、$|v|=\frac{|\omega|}{|k|}=2\pi \frac{\nu}{|k|}=constant$(定数)
これより、次の命題が成立つ。
命題4.6
2つの波の波数の絶対値|k|が等しい(あるいは波長$\lambda$の等しい)ことと
振動数$\nu$(あるいは周期$T$)が等しいこと
は同等である。
波の重ね合わせの原理とその応用
後述(4.4弾性波の力学的考察)するように、
波の運動方程式である波動方程式は線形性 をもつので、
次のような波の重ね合わせが出来る。
媒質のある場所に、1つの波が来たときの変位$ y_1$ と他の波が来たときの変位を$ y_2$ とすると、
この2つの波がこの場所に同時に来た時の媒質の変位は$ y=y_1+y_2$となる。
これを波の重ね合わせの原理という(注参照)。
重ね合わせて出来る波を合成波という。
この原理は、多くの波の現象の分析・解析に応用できる。
(注)数式を用いて正確に述べると次のようになる。
一つの波を $y_1=y_1(x,t)$、他の波を $y_2=y_2(x,t)$ とすると、
この二つの波が同時に起きて出来る波 $y=y(x,t)$ は
$y=y(x,t)=y_1(x,t)+y_2(x,t)$
複雑な形の波
一般の複雑な形の波は、
周期や振幅の異なるいくつかの正弦波を重ね合わせたものと考えることができる。
これについては大学の専門課程で学ぶ(フーリエ解析と呼ばれる)。
干渉
一般に出会った2つの波の変位がともに正(負)ならば、
重ね合わせの原理より、合成波の変位の絶対値は、一層大きくなり、強めあう。
また一方の変位が正で他方が負の時は、合成波の変位の絶対値は小さくなり、弱めあう。
2つ(以上)の波が重なり合って強めあったり弱めあったりする現象を波の干渉という。
様々な干渉現象は、波の重ね合わせの原理によって分析できる。
2つの波源からでる同一の振動数をもつ球面波の干渉
2つの波源からでる同一の振動数をもつ球面波の干渉を考察しよう。(注1参照のこと)
命題4.6 により、両者の波長は等しい。
2つの波源を含むひとつの平面上で考える(あるいは、2次元の球面波を考える)。
ある瞬間に、2つの波の山と山(緑と赤の円の交点)、谷と谷が重なり合った場所では
合成波は時間とともに大きく変動する。
このような点(無数にある)を、合成波の腹という。
一方の波の山と他方の波の谷が重なる場所では、合成波の変位は少ない(注2を参照のこと)。
このような点(無数にある)を、合成波の節という。
(注1)球面波は、波面が球(2次元波の時は円)となる波である。
この波は、波源からあらゆる方向に初期位相と波長と振動数が等しい(従って速さも等しい)波が放射される。
波源から離れるに従い、波は広がっていくので、振幅は減少していく。
しかし、減衰の仕方は方向によらず、同じである。(4.4節を参照のこと)。
2次元の球面波(波面が同心円状の波)は、水面に小石を落とした時に発生する。
波源で方向性のある波を発生しても、
波源から十分離れた場所では球面波とみなしてもよいことが多い。
(注2)2つの波は振動数が同じなので、
2つの波の山と山が重なる点では、時間が進むにつれ、
同時に変位は0になり、次に、同時に谷になる。
こうして、合成波は腹の地点で大きな振幅で振動する。
2つの波の谷と谷が重なる点でも、同様に、合成波の振動は大きくなる。
他方、一方の山と他方の谷が重なる点では、
時間が経過しても絶えず正負が打ち消しあう関係にあるので、
振動の振幅は小さくなる。
2つの波源からの距離を用いた腹と節の条件式
命題4.7
2つの波源が同一周期で同一波長$\lambda$の波を生むとする。
2つの波源の初期時刻における位相角が等しいと仮定する。
(1)両波源からの距離が $l_1$ と $l_2$ の点が合成波の腹になる条件は
$|l_1-l_2|=m \lambda \quad (m=0,1,2,,,,),\qquad \qquad (14)$
(2)両波源からの距離が $l_1$ と $l_2$ の点が合成波の節になる条件は
$|l_1-l_2|=(m+\frac{1}{2} )\lambda \quad (m=0,1,2,,,,),\qquad \qquad (15)$
証明;
(1);両者の行程の差は、$|l_1-l_2|$ であり、これが0か波長の自然数倍のとき、
片方の波が山(谷)ならば、他方も山(谷)になり、波は強めあう。
(2);両者の行程の差が $\frac{1}{2}$ 波長か、それに波長の整数倍を加えたとき、
半波長分位相が異なるので、片方が山の時、他方は谷となり弱めあう。
証明終わり。
定常波と進行波
定常波(standing waveまたはstationary wave)とは、
波形が進行せずその場に止まって振動しているようにみえる波動のことである。
定在波(ていざいは)ともいう。(下記のウィキペディアの記事の冒頭より)。
命題4.8
2つの波を考える。
もし両者の
振幅$A_i(i=1,2)$が等しく、波数ベクトル$k_i(i=1,2)$が等しく、
速度$v_i(i=1,2)$が逆向き($v_1=-v_2$)
ならば、
この2つの波が重なると定常波となる。
証明;
2つの波の共通の振幅をA,波数ベクトルをkとかくと、
命題4.4 より、
$y_1=A\sin {\left(k(x-vt)+\alpha \right) }$ (x軸の正方向に進行)
$y_2=A\sin {\left(k(x+vt)+\beta \right) }$ (x軸の負方向に進行)
で表せる。
両者が重なるときの波形は、重ね合わせの原理から、
$y=y_1 +y_2$
$=A\sin {\left(k(x-vt)+\alpha \right)}+A\sin {\left(k(x+vt)+\beta \right)}$
$\quad$ 三角関数の加法定理(注参照)を用いて、式を簡略化するために、
$\quad$ $\gamma:=\frac{\alpha + \beta}{2}$、$\delta:=\frac{\alpha - \beta}{2}$ という変数を導入すると、
$\quad$ $\alpha=\gamma + \delta $、$\beta=\gamma - \delta $ と表現される。
$\quad$ これらを、上式に代入して、計算を進めると、
$y=A\sin {\left(k(x-vt)+ \gamma + \delta \right)}+A\sin {\left(k(x+vt)+ \gamma - \delta \right)}$
$=A\sin {\left((kx+ \gamma)-(kvt - \delta) \right)}+A\sin {\left(kx+\gamma)+(kvt- \delta) \right)}$
$\quad$ $a:=kx+ \gamma$、$b:=kvt - \delta$ とおくと、
$y=A\sin{(a-b)} + A\sin{(a+b)}$
$\quad$ 三角関数の加法定理を適用すると
$=A\left( (\sin{a} \cos{b}-\sin{b}\cos{a})+ (\sin{a} \cos{b}+\sin{b}\cos{a}) \right)$
$=2A\sin{a} \cos{b}=2A\cos{(kvt - \delta)}\sin{(kx+ \gamma)} $
を得る。
これは波数ベクトルkで、速度が0で、その振幅が $2A\cos{(kvt - \delta)}$(時間とともに振動する)で与えられる定常波である。
証明終わり。
定常波とその腹と節については
定常でない波は進行波という。
(注)
三角関数の加法定理については、
ウィキペディア(三角関数の公式の一覧)を参照のこと。
媒質の端における波の反射、固定端と自由端
波が媒質の終端に達するとそこで反射し、逆方向にすすむ。
反射した波の形は、自由端と固定端では異なる。
実際に観測される波の形は後続の進行波と反射波の合成波である。
固定端と自由端
波の変位量が0に固定されてしまう終端を、固定端という。
反対に、波の変位量の拘束が与えられず自由な値を取れる終端を、自由端という。
例えば、
両端を固定して張った弦のある場所に力を与えて振動を起こさせると、横波が起こる。
横波の変位量は、弦の位置の(巨視的な)変化量である。
弦の両端は固定されているので、位置は変化できず、固定端になる。
媒質の終端が固定されておらず、その部分の媒質が自由に動ける場合が自由端になる。
縦波では、どのような場合に固定端になるのだろうか。
この場合には、波の変位量として、何を選んでいるかで、
同じ端でも固定端にもなり、自由端にもなる。
円管の中の空気の振動(音)を例にして考える。
円管の中の空気のことを、気柱(「4.2 音と音波」で詳述)という。
もし、波長が気柱の直径に比べて大きい時には、
気柱の波は円管に沿って進む平面波と考えられる。
そこで、気柱を進行する平面波を考えて、
閉鎖端と開放端が固定端なのか自由端なのか、考えてみよう。
菅の一方の端Aは壁でふさがれており、他方の端Bは、大気に開放されているとする。
ファイル:GENPHY00010401-03.pdf
閉鎖端A;
波の変位量として、気体の位置変化をとるときには、
閉鎖端では、空気は動けず変位量は常に零なので固定端となる。
ここで波が反射すると、合成波はA端を節とする定常波になる。
ところが、気体の密度・圧力を変位量に選ぶと、
A端では、密度の高い(圧力が大きい)波が進行してきても、
端が塞がれているため、空気が外部にもれず、
波の密度(圧力)に合わせて密度(圧力)は変動する。
波の変位量が自由に変動できるので、自由端になる。
ここで波が反射すると、その合成波はA端を腹とする定常波になる。
開放端B
B端では気圧が大気圧に等しくなるように管内の空気は自由に出入りする。
気柱の中の波がB端に達すると、この気圧を大気圧に維持するため、大気との間に空気が出入りし、
B端が波源となり気柱に反射波が生じる。
この合成波はB端で大気圧に維持される定常波である。
そこで、波の変位量として密度・圧力をとるときには、B端は固定端となり、節となる。
他方、気体の位置変化を変位量としてとると、
B端では気体が自由に動けるため、自由端となり、定常波の腹となる。
図参照のこと。
従って、管の端の開閉より、波の変位量を考慮した、固定端、自由端の区別が、波の性質を考えるときは、重要な概念になる。
固定端での波の反射と合成波
進行波がx軸上を $v=\frac{\omega}{k}$ の速度で進む正弦波
$y_1=A\sin \left(kx-kv t+\theta\right)\qquad \qquad (12)$
を例に、反射波を求める。
固定端では、
波の変位量(横波では位置変化、縦波では密度・圧力変化)を零にするため媒質に、
波の周期と等しく振動する力を与え続ける。
このため固定端を波源となる波が発生し、媒質中を伝わる。
この波は、振動数が進行波と等しく、逆向きに進行するので、
$y_2=B\sin \left(kx+kv t+\theta\right)$、(注参照)
固定端で,$y_1+y_2 \equiv 0$ となるには、$A=B$
すると命題4.5 より
合成波$y_1+y_2$ は定常波となり、その固定端は節になる。
(注)命題4.6 より、振動数が等しければ波数kも等しいことが分かる。
自由端 での波の反射と合成波
この場合には、波は何の障害もなく、自由端の変位量を変化させる。
このため、自由端は波の振動に合わせて、同位相、同振幅で振動する波源となり、
進行波と同振幅、同位相、同周期(振動数)の波を、逆方向に放出する。
すると命題4.5 より、
その合成波は定常波となり。自由端は、その腹になることが分かる。
なお、反射については
を参照のこと。
2つの媒質の境界における波の反射と透過
波面の進行にかんするホイヘンスの原理
ホイヘンスの原理
1678年 C.ホイヘンスが唱えた原理で、波の波面がどのように進行するかを説明するもの。
伝播する波動の波面Wの各点pから初期位相の同じ球面状の二次波(素元波)が出ていると考える。この二次波の位相が同量だけ微小進んだ時の波面$S_p$の包絡面(注1参照)を,次の波面$\tilde{W}$とする。
これを繰返して、波面の進行を求めることができる(注2参照)。
波は波面に垂直方向に進行するので、波の進行方向も求まる。
ホイヘンスは、この原理を用いて、波の反射や屈折現象を説明した。
- ウィキブックス(高等学校理科 物理I 波)の5.2 ホイヘンスの原理
で学んでください。
ホイヘンスの原理の修正やその正しさの証明などの解説は以下をご覧ください。
(注1)面$\tilde{W}$が2次波の包絡面とは、$\tilde{W}$のどの点qも、ある2次波の波面$S_p$ と接していること。
(注2)波面の各点が波源となる球面波の微小時間後の包絡面は
波の進行方向だけでなく、逆向きにもできてしまう。
これを避けるため、波面の各点が波源となって発生するのは球面波でなく、
その一部(進行方向の半球だけ)などの修正が考えられた。
平面波の反射の法則
平面状の鏡や壁にあたった波は、反射する。
入射角と反射角
鏡に当たる波を入射波、反射して出ていく波を反射波という。
入射波の進行方向と鏡の垂線(注参照)が作る角度を入射角という。
反射角も同様に定義する。
(注)鏡の垂線とは、鏡と直交する直線のこと。すなわち、鏡のうえの、どんな直線とも直交する直線のこと。
反射の法則
反射の法則
波の入射角と反射角は一致する。
水面などのように、2つの媒質の平面状の境界では
波の一部が反射して、同一媒質中を進行し、
他は、進行方向を変えて他の媒質に進入する(屈折という)。
この場合にも反射については、同じ法則が成立つ。
反射法則は、波の速さが同一媒質中では変わらないことから、
ホイヘンスの原理を用いて証明できる。
屈折にかんするスネルの法則
この法則を、ホイヘンスの原理から導いてください。
回折
波がその進行方向にある障害物の背後に回り込んで伝わっていく現象のことを、回折という。
多数の波源の干渉(重ね合わせ)の結果おこる現象である。
従って干渉と回折は本質は同じ現象で、単に波源の数の大小の違いである。
その境界もはっきり定められない。
この現象もホイヘンスの原理と重ね合わせの原理で説明できる。
例えば、壁に小さな穴が開いていると、
平面波が壁に進入したとき、この穴の部分の媒質が振動し、新たな一つの波源となり、壁の向こう側に球面波を作る。
こうして壁の影にも波は回り込む。
他方、壁に垂直方向に進む平面波が大きな壁の穴に達すると、穴の各点が同一初期位相の波源となる。
この波源の波は重ね合わせると
進入波と垂直方向の壁側の地点では、(伝達時間の差から)位相が少しづつ違う波の和となり、殆ど変位を生じない。
一方、進入波の進行方向の壁の向こう側では、ある程度壁から離れると、各波源から来る波の位相が
ほぼ等しくなるため、波は強めあう。
このため、平行波は、穴を通り抜け、まっすぐ進行する。
ウィキブックス(高等学校理科 物理I 波/波の性質)の「5.4 回折」を参照のこと。