輸送問題
提供: Internet Web School
| 40 行: | 40 行: | ||
作成したデータは以下の通りである. | 作成したデータは以下の通りである. | ||
| + | |||
| + | [[ファイル:LP-Fig20 ページ 04.jpg|500px]] | ||
ソルバーのパラメータ 入力は以下の通りである. | ソルバーのパラメータ 入力は以下の通りである. | ||
| + | |||
| + | [[ファイル:LP-Fig20 ページ 06.jpg|500px]] | ||
ソルバーによる結果は以下の通りである. | ソルバーによる結果は以下の通りである. | ||
| + | |||
| + | [[ファイル:LP-Fig20 ページ 08.jpg|500px]] | ||
$x_{1,1}=65,x_{1,2}=5,x_{1,3}=0,x_{2,1}=0,x_{2,2}=40,x_{2,3}=50$ | $x_{1,1}=65,x_{1,2}=5,x_{1,3}=0,x_{2,1}=0,x_{2,2}=40,x_{2,3}=50$ | ||
2020年11月27日 (金) 12:23時点における版
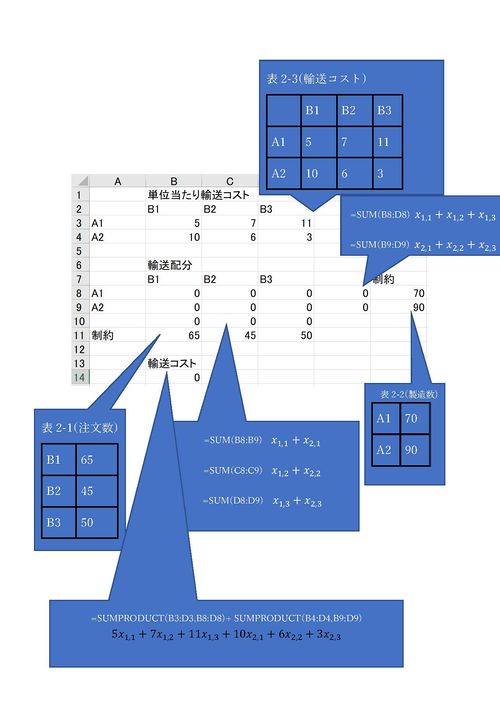
製品を2つの工場A1,A2で製造し3社B1,B2,B3に納入している企業がある.これら3社からの注文は表2-1の通りである.この注文に応じるため表2-2のように工場A1,A2で製品を製造する. 製造した製品を工場A1,A2からそれぞれB1,B2,B3に輸送する際の1単位当たりのコストは表2-3の通りである. 3社B1,B2,B3からの注文を充足し,かつ,輸送コストを最小にするには, 工場A1,A2から3社B1,B2,B3への輸送数をどのように配分すれば良いか. 工場\(A_i\)から注文先\(B_j\)への製品の輸送量を
\(x_{i,j}\left(\ i=1,2\ j=1,2,3\right)\) で表すと,
表2-1から工場\(A_1,A_2\)から注文先\(B_1,B_2,B_3\)への輸送について制約条件式
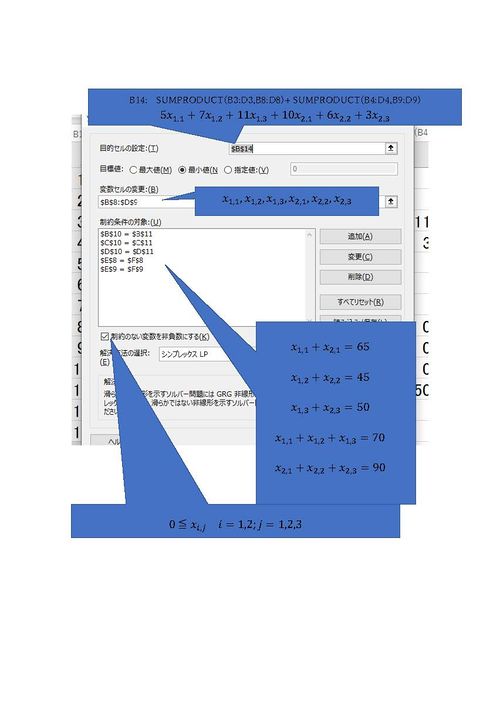
\( x_{1,1}+x_{2,1}=65 \\ x_{1,2}+x_{2,2}=45 \\ x_{1,3}+x_{2,3}=50 \)
を満たす. また,表2-2から工場\(A_1,A_2\)の製造量について制約条件式
\( x_{1,1}+x_{1,2}+x_{1,3}=70 \\ x_{2,1}+x_{2,2}+x_{2,3}=90 \)
を満たす.さらに製造量は非負であるから
\( {0\leqq x}_{i,j} i=1,2;j=1,2,3 \)
これらの制約条件の下で輸送コストの総和
\( {5x}_{1,1}+{7x}_{1,2}+11x_{1,3}+{10x}_{2,1}+{6x}_{2,2}+{3x}_{2,3} \)
の最小値を求める.この問題も生産計画と同様 線形計画法 に属する.
ファイル:輸送問題.pdfにMicrosoft Excel のソルバーを用いたこの問題の解法例を示す.
作成したデータは以下の通りである.
ソルバーのパラメータ 入力は以下の通りである.
ソルバーによる結果は以下の通りである.
$x_{1,1}=65,x_{1,2}=5,x_{1,3}=0,x_{2,1}=0,x_{2,2}=40,x_{2,3}=50$
のとき輸送コストの総和
$x_{1,1}+7x_{1,2}+11x_{1,3}+10x_{2,1}+6x_{2,2}+3x_{2,3}$
が最小値750になることを示している. 表2-1,表2-2の制約条件を満たしている.