数学・解析/指数関数
提供: Internet Web School
(版間での差分)
(ページの作成: 数学・解析 = 目次 = * Wikiポータル 数学 * 単位円 * 三角関数 = …) |
|||
| 5 行: | 5 行: | ||
* [[wikipedia_ja:Portal:数学|Wikiポータル 数学]] | * [[wikipedia_ja:Portal:数学|Wikiポータル 数学]] | ||
| - | * [[wikipedia_ja: | + | * [[wikipedia_ja:指数関数|指数関数]] |
| - | * [[wikipedia_ja: | + | * [[wikipedia_ja:冪根|冪根]] |
= 解説 = | = 解説 = | ||
| - | * [[wikipedia_ja: | + | * [[wikipedia_ja:冪乗#.E6.8C.87.E6.95.B0.E3.81.AE.E6.8B.A1.E5.BC.B5.E3.81.A8.E6.8C.87.E6.95.B0.E6.B3.95.E5.89.87|指数の拡張と指数法則]] ※引用元:Wikipedia |
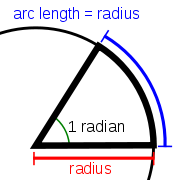
[[File:180px-Radian_cropped_color.svg.png|thumb|半径と弧の長さが等しくなる角度(約57.3度)]] | [[File:180px-Radian_cropped_color.svg.png|thumb|半径と弧の長さが等しくなる角度(約57.3度)]] | ||
| 21 行: | 21 行: | ||
== CAIテスト == | == CAIテスト == | ||
| - | * [[cai_ja: | + | * [[cai_ja:GENANA00010006|CAIテストのページへ]] |
2010年9月14日 (火) 01:12時点における版
目次
解説
- 指数の拡張と指数法則 ※引用元:Wikipedia
1つの円において 半径に等しい長さの弧に対する中心角 をとり、この中心角を α とします。このαは円の半径に関係しない一定の角です。この角を 1ラジアン または 1弧度 といい、これを単位とする角の表し方を 弧度法 といいます。
- 1ラジアン = 180°/π 1°= π/180 ラジアン