物理/8章の付録
提供: Internet Web School
(→ 対数関数) |
(→ 「7.6 7章の付録」) |
||
| (間の64版分が非表示) | |||
| 1 行: | 1 行: | ||
| - | = | + | = 「7.6 この章の付録」= |
== 問の解答== | == 問の解答== | ||
=== 問 === | === 問 === | ||
$\lim_{n\to \infty}(1+\frac{1}{n})^n$ が存在し、2より大きく3以下であることを証明する。<br/> | $\lim_{n\to \infty}(1+\frac{1}{n})^n$ が存在し、2より大きく3以下であることを証明する。<br/> | ||
| - | + | (1)準備; 2項定理を用いた展開<br/> | |
$a_n\triangleq (1+\frac{1}{n})^{n} \qquad (n は自然数)$ とおく。<br/> | $a_n\triangleq (1+\frac{1}{n})^{n} \qquad (n は自然数)$ とおく。<br/> | ||
すると、 | すると、 | ||
| 13 行: | 13 行: | ||
ここで ${}_n\mathrm{C}_{m}$ は、n個のものからm個取り出す取り出し方の総数で、<br/> | ここで ${}_n\mathrm{C}_{m}$ は、n個のものからm個取り出す取り出し方の総数で、<br/> | ||
mが1以上でn 以下の自然数の時は<br/> | mが1以上でn 以下の自然数の時は<br/> | ||
| - | ${}_n\mathrm{C}_{m}=\frac{n!}{m!(n-m)!} \qquad \qquad (2)$<br/> | + | ${}_n\mathrm{C}_{m}=\frac{n!}{m!\ (n-m)!} \qquad \qquad (2)$<br/> |
ここで、m が1以上の自然数の時は $ m!\triangleq 1\cdot 2\cdot 3 \cdots (m-1)\cdot m$<br/> | ここで、m が1以上の自然数の時は $ m!\triangleq 1\cdot 2\cdot 3 \cdots (m-1)\cdot m$<br/> | ||
mが零の時は $\quad 0!\triangleq 1 $ と定義。<br/><br/> | mが零の時は $\quad 0!\triangleq 1 $ と定義。<br/><br/> | ||
すると、<br/> | すると、<br/> | ||
| - | ${}_n\mathrm{C}_{0}=\frac{n!}{0!n!}=1\qquad \qquad (3)$ <br/> | + | ${}_n\mathrm{C}_{0}=\frac{n!}{0!\ n!}=1\qquad \qquad (3)$ <br/> |
| - | $m \geq 1$のとき、${}_n\mathrm{C}_{m} =\frac{n!}{m!(n-m)!}=\frac{n\cdot (n-1)\cdot (n-2) \cdots \Bigl(n-(m-1)\Bigr) }{m!} \qquad (4)$<br/> | + | $m \geq 1$のとき、${}_n\mathrm{C}_{m} =\frac{n!}{m!\ (n-m)!}=\frac{n\cdot (n-1)\cdot (n-2) \cdots \Bigl(n-(m-1)\Bigr) }{m!} \qquad (4)$<br/> |
式(1)に式(2)を代入し,式(3)、(4)を利用して計算すると<br/> | 式(1)に式(2)を代入し,式(3)、(4)を利用して計算すると<br/> | ||
$a_n = 1+\sum_{m=1}^{n}\frac{n(n-1)(n-2)\cdots \Bigl(n-(m-1)\Bigr)}{m!}1^{n-m}(\frac{1}{n})^m $<br/> | $a_n = 1+\sum_{m=1}^{n}\frac{n(n-1)(n-2)\cdots \Bigl(n-(m-1)\Bigr)}{m!}1^{n-m}(\frac{1}{n})^m $<br/> | ||
| 103 行: | 103 行: | ||
== 指数関数と対数関数 == | == 指数関数と対数関数 == | ||
| - | === | + | === 正の実数の累乗の指数の拡張 === |
| - | a | + | ==== 実数の累乗(自然数乗) ==== |
| - | $a^1=a,\quad a^2=a\cdot a,\quad a^3=a^2\cdot a=a\ | + | $a$ を任意の実数、$n$ を2以上の自然数とする。<br/> |
| + | $a^1=a,\quad a^2=a\cdot a,\quad a^3=a^2\cdot a=a\cdot a\cdot a ,\quad \cdots \quad a^n=a^{n-1}\cdot a, \cdots$<br/> | ||
を総称して、a の'''累乗'''と呼ぶ。<br/> | を総称して、a の'''累乗'''と呼ぶ。<br/> | ||
| - | $a^n$ | + | $a^n$ を$a $ の n 乗 、$n$ をその指数と呼ぶ。<br/> |
| - | ''' | + | |
| - | a, | + | ===== 実数の自然数乗の3つの計算規則===== |
| + | 累乗が次のような計算規則を満たすことは、容易に証明できる。<br/> | ||
| + | '''命題3'''<br/> | ||
| + | $ a,b $ を任意の実数、$ m, n $ を任意の自然数とすると、<br/> | ||
(1) $a^{m}a^{n} = a^{m+n} $<br/> | (1) $a^{m}a^{n} = a^{m+n} $<br/> | ||
(2) $(a^{m})^n =a^{m n} $<br/> | (2) $(a^{m})^n =a^{m n} $<br/> | ||
(3) $(ab)^n = a^n b^n $<br/><br/> | (3) $(ab)^n = a^n b^n $<br/><br/> | ||
| - | + | 証明は、累乗の定義と積の交換法則から容易にできるので省略する。<br/> | |
| + | ===== 指数関数とn次関数 ===== | ||
| + | $a$ を正の実数とするとき、累乗$a^{\alpha}$ の <br/> | ||
| + | $\alpha$ を独立変数とするか、$a$ を独立変数にするかで、<br/> | ||
| + | 次の2種の関数が定まる。<br/><br/> | ||
| + | '''定義'''<br/> | ||
| + | $a$ を正の実数, $\alpha$を自然数とするとき、次の2つの関数を考える。<br/> | ||
| + | 1)$f_{a}; ({\bf N} \ni) \alpha \to a^{\alpha} \bigl(\in {\bf R}^{+}\triangleq (0,\infty)\bigr)$<br/> | ||
| + | これは、指数を変数とする関数なので、'''指数関数'''という。<br/> | ||
| + | 2)$g_{\alpha}; ({\bf R}^{+}\ni) a \to a^{\alpha} (\in {\bf R}^{+})$<br/> | ||
| + | これは、$\alpha$次の単項関数である。<br/><br/> | ||
| + | '''命題 指数関数の性質'''<br/> | ||
| + | 指数関数$f_{a}(\alpha )=a^{\alpha} \quad (\alpha \in {\bf N})$ は次の性質を持つ。<br/> | ||
| + | 1)$0 \lt a \lt 1$のとき、${\bf N}$から${\bf R}^{+}$への狭義単調減少の連続関数で、$\lim_{\alpha \to \infty ,\alpha \in {\bf N} } a^{\alpha} = 0$<br/> | ||
| + | 2)$1 \lt a$のとき、${\bf N}$から${\bf R}^{+}$への狭義単調増加の連続関数 | ||
| + | で、<br/> | ||
| + | $\lim_{\alpha \to \infty ,\alpha \in {\bf N} } a^{\alpha} = \infty$<br/> | ||
| + | 連続性以外は、明らかなので証明は省略する。<br/> | ||
| + | 自然数全体の集合${\bf N}$は離散集合なので、<br/> | ||
| + | そのうえで定義された任意の関数は連続となる。<br/> | ||
| + | 「8.2 解析入門(1)実数の性質、連続関数、微分 $\quad$ 「1.3 関数とその連続性」の[[物理/解析入門(1)実数の性質、連続関数,微分と導関数#関数とその連続性|「1.3.2 関数の極限と連続性」]]を参照のこと。<br/><br/> | ||
| + | '''命題''' $n$次の単項関数の性質<br/> | ||
| + | $\alpha= n \in {\bf N}$ とする。<br/> | ||
| + | $n$次の単項関数$g_{n}(a)=a^{n} \quad (a \in {\bf R}^{+})$ は<br/> | ||
| + | ${\bf R}^{+}$から${\bf R}^{+}$への狭義単調増加の連続関数で、<br/> | ||
| + | $\lim_{a\to 0,a \in {\bf R}^{+} } a^{n} = 0$<br/> | ||
| + | $\lim_{a\to \infty,a\in {\bf R}^{+} } a^{n} = \infty$<br/> | ||
| + | である。<br/> | ||
| + | 証明<br/> | ||
| + | ${\bf R}^{+}$上では狭義単調増加であることは容易に示せる。<br/> | ||
| + | 連続性については、$\lim_{\delta \to 0}(a+\delta)^n = a^n $ であることを示せばよい。<br/> | ||
| + | 例えば、2項定理で$(a+\delta)^n $ を展開して極限をとればよい。 | ||
| + | |||
| + | ===== この節の目的 ===== | ||
| + | この節の目的は、累乗にかんする計算規則を満たすようにしながら、<br/> | ||
| + | 累乗の指数を実数まで拡張することである。<br/> | ||
| + | しかし $a$ が負数だと、指数を有理数に拡張するとき不都合が起きてしまう。<br/> | ||
| + | 例えば <br/> | ||
| + | $\frac{1}{2}$ の時, $a^{\frac{1}{2}}= \sqrt{a}$ は実数でなく虚数となり、<br/>実数値関数の枠組みに収まらなくなる。<br/> | ||
| + | そこで、このような不都合が起こらないように 今後は$a$ を正の実数に限定し、<br/>次の計算規則を満たすようにしながら、指数を自然数から整数、整数から有理数、有理数から実数へと順に拡張していく。<br/><br/> | ||
'''累乗に関する計算規則'''<br/> | '''累乗に関する計算規則'''<br/> | ||
| - | a, | + | $ a, b $ を任意の正の実数、$\alpha,\quad \beta$を指数とすると、<br/> |
(1) $a^{\alpha}a^{\beta} = a^{\alpha+\beta} \qquad \qquad \qquad (累乗規則1)$<br/> | (1) $a^{\alpha}a^{\beta} = a^{\alpha+\beta} \qquad \qquad \qquad (累乗規則1)$<br/> | ||
(2) $(a^{\alpha})^\beta =a^{\alpha \beta} \qquad \qquad \qquad (累乗規則2)$<br/> | (2) $(a^{\alpha})^\beta =a^{\alpha \beta} \qquad \qquad \qquad (累乗規則2)$<br/> | ||
(3) $(ab)^\beta = a^\beta b^\beta \qquad \qquad \qquad (累乗規則3)$<br/><br/> | (3) $(ab)^\beta = a^\beta b^\beta \qquad \qquad \qquad (累乗規則3)$<br/><br/> | ||
| - | + | 計算規則(3)を守ろうとすると、$1^\beta \equiv 1$ と定めなければならないことが分かる。<br/> | |
| - | + | 何故ならば $b=1$の時、$a^\beta = (a・1)^\beta = a^\beta 1^\beta $ となり、 $a^\beta \neq 0$ であるから。<br/> | |
| - | + | そこで 今後は常に $1^\beta \equiv 1$ と定め、 $a \neq 1$ の場合だけを考察する。<br/><br/> | |
| - | + | 本節のもう一つの目的は、指数の拡張に伴い累乗に伴う2つの関数<br/> | |
| + | $f_{a}(\alpha)=a^\alpha$ と$g_{\alpha}(a)=a^\alpha$ の性質が、どのようになるか考察する事である。 | ||
| + | |||
==== 指数の整数への拡張 ==== | ==== 指数の整数への拡張 ==== | ||
| - | + | 任意の正の実数$a(\neq 0,1)$ を考える。<br/> | |
| - | + | $a$の累乗の指数を、累乗に関する3つの規則が成り立つようにしながら、整数に拡張しよう。<br/> | |
| - | $a \ | + | まず、規則(1)を守ろうとすれば <br/> |
| - | $a^ | + | $a^0 = 1 \qquad \qquad \qquad (4) $ <br/> |
| - | $\ | + | と定義しなければならないことが分かる。<br/> |
| - | $\ | + | 何故ならば、$n\in {\bf N}$ の時、<br/> |
| - | + | $a^{n} = a^{n+0}= a^n a^0 $ <br/> | |
| - | + | となり、 $a^n \neq 0$ だから両辺を $a^n$ で割ればよい。<br/> | |
| - | + | 次に任意の自然数 n に対して、<br/> | |
| - | + | $a^{-n}$ を累乗に関する規則(1)を満たすように定義しよう。<br/> | |
| - | + | $a^{-n}a^n = a^{-n+n} = a^0 = 1$<br/> | |
| - | + | 両辺を $a^n$ で割れば<br/> | |
| - | $a^ | + | $a^{-n} = \frac{1}{a^n} \qquad \qquad \qquad(5)$<br/><br/> |
| - | + | 命題<br/> | |
| - | + | 式(4),(5)に従って指数を整数に拡大すると、<br/> | |
| + | 3つの累乗の規則はすべて成立する。<br/> | ||
| + | 証明<br/> | ||
| + | 指数が負のときは式(5)を用いて、指数が自然数の式に書き直し、<br/> | ||
| + | 指数が自然数のときに成り立つことが分かっている3つの計算規則を使って式の変形をすれば良い。<br/> | ||
| + | 計算規則の(1)の証明だけを示そう。<br/> | ||
| + | (1)$\alpha ,\beta $ を任意の整数とすると、<br/> | ||
| + | $ a^{\alpha}a^{\beta} = a^{(\alpha +\beta) }$ であることを示す。<br/> | ||
| + | (ケース1)指数の一方が正の整数(自然数)で、他方が負の整数の時<br/> | ||
| + | $m,n$ を自然数として、<br/> | ||
| + | $ a^{m}a^{-n} = a^{m-n}$ を示せばよい。<br/> | ||
| + | 式(5)から<br/> | ||
| + | $ a^{m}a^{-n} = \frac{a^m}{a^n} \qquad \qquad \qquad (6)$<br/> | ||
| + | $m \gt n$ 、$m=n$ 、$m \lt n$ という3つの場合に分けて証明する。<br/> | ||
| + | 1)$m \gt n$ の時<br/> | ||
| + | 割り算を実行すると$\frac{a^m}{a^n}=a^{m-n} $<br/> | ||
| + | この式と、式(6)から、$ a^{m}a^{-n} = a^{m-n} $<br/> | ||
| + | 2) $m=n$ の時<br/> | ||
| + | $\frac{a^m}{a^n}= 1 = a^{m-n} $<br/> | ||
| + | この式と、式(6)から、$ a^{m}a^{-n} = a^{m-n} $<br/> | ||
| + | 3) $m \lt n$ の時<br/> | ||
| + | 割り算を実行すると、<br/> | ||
| + | $\frac{a^m}{a^n}= \frac{1}{a^{(n-m)}}$<br/> | ||
| + | $=a^{m-n} $<br/> | ||
| + | (ケース2)両方の指数が負の整数の時<br/> | ||
| + | $a^{-m}a^{-n} = a^{-m-n}$ を示せばよい。<br/> | ||
| + | $a^{-m}a^{-n} = \frac{1}{a^m}\frac{1}{a^n}=\frac{1}{a^m a^n}=\frac{1}{a^{(m+n)}} | ||
| + | =a^{-m-n}$<br/> | ||
| + | |||
==== 指数の有理数への拡張 ==== | ==== 指数の有理数への拡張 ==== | ||
| - | + | これ以降、有理数全体のなす集合を${\bf Rat}$とかく。<br/> | |
| - | + | $ a (\neq 1)$ を任意の正の実数、 $\frac{m}{n}$ を任意の有理数のとき、<br/> | |
| - | $a^{\frac{m}{n}} = a^{\frac{-m}{-n}}$ | + | $ a $ の有理数乗 $a^{\frac{m}{n}}$ を、計算規則を満たすように定義しよう。<br/><br/> |
| + | 指数n を任意の自然数(正の整数)、 m を任意の整数と仮定してよい。<br/> | ||
| + | $\qquad $(注)nが負の時は$a^{\frac{m}{n}} = a^{\frac{-m}{-n}}$ なので、<br/> | ||
| + | $\qquad \quad -n,-m $を改めて$n,m$ と置けば良い。$\Box$<br/> | ||
累乗規則(2)を満たすように定義するには、<br/> | 累乗規則(2)を満たすように定義するには、<br/> | ||
$(a^{\frac{m}{n}})^{n} = (a^{\frac{m}{n}})^{\frac{n}{1}} = a^{m}$ <br/>でなければならない。<br/> | $(a^{\frac{m}{n}})^{n} = (a^{\frac{m}{n}})^{\frac{n}{1}} = a^{m}$ <br/>でなければならない。<br/> | ||
| - | + | これは、$a^{\frac{m}{n}}$ が $a^{m}$ のn乗根であることを示す。<br/> | |
| - | + | しかしnが偶数のときは、$-a^{\frac{m}{n}}$ も$a^{m}$ のn乗根となるので、 | |
| + | 正のn乗根 のほうを、$a^{\frac{m}{n}}$ とかく。<br/><br/> | ||
| + | '''定義''' 正の実数の有理数乗<br/> | ||
| + | $a$を正の実数とする。<br/> | ||
| + | $a^{\frac{m}{n}}$ とは、<br/> | ||
| + | $a^{m}$ の正のn乗根である。<br/> | ||
| + | すなわち、 <br/> | ||
| + | $(a^{\frac{m}{n}})^{n} =a^{m} $を満たす正の実数である。<br/><br/> | ||
最初に、この定義できちんと正の実数が一つだけ決まることを証明しよう。<br/> | 最初に、この定義できちんと正の実数が一つだけ決まることを証明しよう。<br/> | ||
| - | + | $a=1$のときは、n乗すると1になる正数は1だけなので<br/> | |
| + | $1^{\frac{m}{n}}=1 $<br/> | ||
| + | であることが分かるので、$a \neq 1$ の場合を考える。<br/> | ||
'''命題3'''<br/> | '''命題3'''<br/> | ||
| - | + | $a \neq 0,1$ を任意の正の実数、$ m$ を任意の整数,$n$を任意の自然数とする。<br/> | |
| - | + | すると、n 乗すると $a^{m}$ になる正の実数 $ b $ (i.e. $\quad b^n = a^{m}$)が存在し、ただ一つに限る。<br/> | |
| - | + | 証明<br/> | |
| + | (1) 存在性<br/> | ||
$ f(x) \triangleq x^n $ という、零と正の実数の上で定義された、関数を考える。 | $ f(x) \triangleq x^n $ という、零と正の実数の上で定義された、関数を考える。 | ||
<br/> | <br/> | ||
この関数はxが増加するにつれて、連続的に、零から正の無限大に狭義に単調に増加(注参照)していく。<br/> | この関数はxが増加するにつれて、連続的に、零から正の無限大に狭義に単調に増加(注参照)していく。<br/> | ||
| - | + | そこで、$B\triangleq \{x \in [0,\infty)\ |\ x^n \leq a^{m} \}$ という集合を考える。<br/> | |
| - | + | この集合は、上に有界な区間になり、実数の連続性から上限(sup)$b$を持つ。<br/> | |
| - | + | この時、$ b \in B, \quad b^n = a^{m}$ であることを示そう。<br/> | |
| - | + | $b$ が集合$B (\in {\bf R})$の上限なので、任意の自然数nに対して、<br/> | |
| - | + | $0 \leq b - b_{n} \lt \frac{1}{n} $ <br/> | |
| - | + | を満たす $ b_{n} \in B $ が存在する。<br/> | |
| - | + | 明らかに<br/> | |
| - | + | $ \lim_{n \to \infty}b_{n} = b $<br/> | |
| - | <br/> | + | すると、関数 $ f(x) \triangleq x^n $ は連続なので、 |
| + | $ \lim_{n \to \infty}b_{n}^n = b^n \qquad \qquad \qquad (a)$<br/> | ||
| + | ところが$ b_{n} \in B \triangleq \{x \in [0,\infty)|x^n \leq a^{m} \}$なので、<br/> | ||
| + | $ b_{n}^n \leq a^{m} \qquad \qquad \qquad (b)$<br/> | ||
| + | 式(a)、(b) から、$ b^n \leq a^{m}$ がえられるので、<br/> | ||
| + | $ b \in B$<br/> | ||
| + | が示せた。(従って、Bは閉区間 [o,b] である。)<br/> | ||
| + | $b^n = a^{m}$ であることを背理法を使って示そう。<br/> | ||
| + | もし、$b^n \lt a^{m}$ だとすると、関数 $ f(x) = x^n $ は連続なので<br/> | ||
| + | 充分小さな正の実数$\delta$ をとると、$(b + \delta) ^n \lt a^{m}$ を満たす。<br/> | ||
| + | すると $(b + \delta) \in B$ となり、<br/> | ||
| + | $b$が B の上限であることに矛盾してしまう。<br/> | ||
| + | 故に、背理法により、$b^n = a^{m} $ が証明できた。<br/> | ||
| + | (2)一意性<br/> | ||
| + | 関数 $ f(x) = x^n $ は狭義の単調増加関数なのでb以外の数b'($\neq b$)では、<br/> | ||
| + | ${b'}^n \neq b^n =a^m$<br/> | ||
| + | (証明終り) $ \qquad \qquad \Box$<br/> | ||
(注) 関数fが狭義単調増加とは、$ x \lt y \Rightarrow f(x) \lt f(y) $ を満たすこと。<br/><br/> | (注) 関数fが狭義単調増加とは、$ x \lt y \Rightarrow f(x) \lt f(y) $ を満たすこと。<br/><br/> | ||
'''命題4'''<br/> | '''命題4'''<br/> | ||
| - | 任意の正の実数 $a$ にたいして、その有理数乗を上記のように定義すると<br/> | + | 任意の正の実数 $a \neq 1$ にたいして、その有理数乗を上記のように定義すると<br/>3つの累乗規則 (1)~(3) が成り立つ。<br/> |
| - | 3つの累乗規則 (1)~(3) が成り立つ。<br/> | + | |
証明; | 証明; | ||
| - | + | 1) 累乗規則(1)が成り立つことを示す。<br/> | |
2個の有理数の指数を 自然数$n,\quad \tilde{n}$と整数$m,\quad \tilde{m}$ を用いて、<br/> | 2個の有理数の指数を 自然数$n,\quad \tilde{n}$と整数$m,\quad \tilde{m}$ を用いて、<br/> | ||
$\alpha = \frac{m}{n},\quad \beta = \frac{\tilde{m}}{\tilde{n}}$と表現する。<br/> | $\alpha = \frac{m}{n},\quad \beta = \frac{\tilde{m}}{\tilde{n}}$と表現する。<br/> | ||
| 177 行: | 278 行: | ||
この左辺を $b \triangleq a^{\frac{m}{n}}a^{\frac{\tilde{m}}{\tilde{n}}}$,<br/> | この左辺を $b \triangleq a^{\frac{m}{n}}a^{\frac{\tilde{m}}{\tilde{n}}}$,<br/> | ||
右辺を $c \triangleq a^{\frac{m}{n}+\frac{\tilde{m}}{\tilde{n}}}$ とおく。<br/> | 右辺を $c \triangleq a^{\frac{m}{n}+\frac{\tilde{m}}{\tilde{n}}}$ とおく。<br/> | ||
| - | $b^{n \tilde{n}} = c^{n \tilde{n}} \qquad \qquad \qquad ( | + | $b^{n \tilde{n}} = c^{n \tilde{n}} \qquad \qquad \qquad (a)$ <br/> |
であることを示せば、$b = c$ が得られ,<br/> | であることを示せば、$b = c$ が得られ,<br/> | ||
累乗規則(1)が成立することが分かる。<br/> | 累乗規則(1)が成立することが分かる。<br/> | ||
| 199 行: | 300 行: | ||
実数の有理数乗の定義から、<br/> | 実数の有理数乗の定義から、<br/> | ||
$ = a^{m\tilde{n} + n\tilde{m}} = b^{n \tilde{n}}$<br/> | $ = a^{m\tilde{n} + n\tilde{m}} = b^{n \tilde{n}}$<br/> | ||
| - | + | これで、式(a)が示され、累乗規則(1)が成り立つことが証明できた。<br/> | |
| - | + | 2)累乗規則(2)と累乗規則(3)が成り立つことは読者がしてください。<br/> | |
| - | + | ||
| - | + | ||
証明終わり。<br/><br/> | 証明終わり。<br/><br/> | ||
| - | 指数が有理数の場合, | + | 指数が有理数の場合,命題2は次のように拡張出来る。<br/><br/> |
'''命題5'''<br/> | '''命題5'''<br/> | ||
| - | + | ${\bf Rat}$の上で定義される関数<br/> | |
| - | $f_a(\alpha) \triangleq a^{\alpha} \qquad (\alpha | + | $f_a(\alpha) \triangleq a^{\alpha} \qquad (\alpha \in {\bf Rat})$を考える。<br/> |
| - | + | 1)$a$ を1より大きい正の実数とすると、<br/> | |
| - | + | ||
| - | + | ||
| - | + | ||
$f_a$は単調増大で<br/> | $f_a$は単調増大で<br/> | ||
| - | $\lim_{\alpha \to \infty}f_a(\alpha) = \ | + | $\lim_{\alpha \to \infty,\alpha \in {\bf Rat}}a^{\alpha} = \infty \quad \lim_{\alpha \to -\infty}f_a(\alpha) = 0 $ <br/> |
| - | + | 2)$a$ が1より小さい正の実数のとき、<br/> | |
| + | $f_a$は単調減少し、<br/> | ||
| + | $\lim_{\alpha \to \infty,\alpha \in {\bf Rat}}f_a(\alpha) = 0\quad \lim_{\alpha \to -\infty,\alpha \in {\bf Rat}}f_a(\alpha) = \infty $ <br/> | ||
| + | 3)$a = 1$ のとき、$f_a \equiv 1$<br/> | ||
証明<br/> | 証明<br/> | ||
| - | 証明終わり<br/> | + | 1)のみ証明する。2)の場合も同様に証明できる。<br/> |
| + | ① $\frac{m}{n} \lt \frac{m'}{n'} ,\quad n,m \in {\bf N} $ とすると、<br/> | ||
| + | $a^{\frac{m}{n}} \lt a^{\frac{m'}{n'}}$ を示そう。<br/> | ||
| + | $\alpha \triangleq a^{\frac{m'}{n'}} \div a^{\frac{m}{n}} \gt 1$<br/> | ||
| + | を示せばよい。<br/> | ||
| + | 正数の有理数乗の計算規則から、<br/> | ||
| + | $\alpha \triangleq a^{\frac{m'}{n'}} \div a^{\frac{m}{n}}=a^{\frac{m'}{n'}-\frac{m}{n}}$<br/> | ||
| + | $=a^{ \frac{m'n-n'm}{n'n} }$<br/> | ||
| + | 故に、<br/> | ||
| + | ${\alpha}^{n'n} = a^{m'n-n'm}$<br/> | ||
| + | $\qquad \frac{m}{n} \lt \frac{m'}{n'}$ から、<br/> | ||
| + | $\qquad m'n-n'm \gt 0 $なので、$a^{m'n-n'm} \gt 1$であり<br/> | ||
| + | $ \gt 1$<br/> | ||
| + | 故に、 ${\alpha}^{n'n} \gt 1$<br/> | ||
| + | 自然数乗すると1より大きくなる正の実数は1より大きい実数しかないので、 | ||
| + | $\alpha \gt 1$ が得られた。<br/> | ||
| + | ② $\lim_{\alpha \to \infty,\alpha \in {\bf Rat}}a^{\alpha}= \infty $を示そう。<br/> | ||
| + | 関数 $f_a(\alpha)$ は単調増加(①で証明)なので、<br/> | ||
| + | $\lim_{n \to \infty,n \in {\bf N}}a^n = \infty $<br/> | ||
| + | を示せばよいが、これは自明である。<br/> | ||
| + | ③ $\lim_{\alpha \to -\infty,\alpha \in {\bf Rat}}f_a(\alpha) = 0 $ <br/> | ||
| + | も、同様にして示せる。<br/> | ||
| + | 証明終わり $\qquad \qquad \qquad \Box$ <br/><br/> | ||
| + | 以上の結果をまとめて、次の定理を得る。<br/> | ||
| + | |||
| + | $\Large {\bf{定理1}}$<br/> | ||
| + | $a \neq 0,1$ の正の実数とする。<br/> | ||
| + | (1)$ a $ の有理数乗 $a^{\frac{m}{n}}\quad(m;整数、n \in {\bf N})$ を$a^{m}$の正の$n$乗根で定義すると、<br/> | ||
| + | '''累乗に関する計算規則'''<br/> | ||
| + | $ a, b $ を任意の正の実数、$\alpha,\beta \in {\bf Rat} $を指数とすると、<br/> | ||
| + | $\quad$ 1) $a^{\alpha}a^{\beta} = a^{\alpha+\beta} \qquad \qquad (累乗規則1)$<br/> | ||
| + | $\quad$ 2) $(a^{\alpha})^\beta =a^{\alpha \beta} \qquad \qquad (累乗規則2)$<br/> | ||
| + | $\quad$ 3) $(ab)^\beta = a^\beta b^\beta \qquad \qquad (累乗規則3)$<br/><br/> | ||
| + | を満たす。<br/><br/> | ||
| + | (2)${\bf Rat}$の上で定義される関数<br/> | ||
| + | $f_a(\alpha) \triangleq a^{\alpha} \qquad (\alpha \in {\bf Rat})$を考えると、<br/> | ||
| + | $\quad$1)$a\gt 1$ のとき、 $f_a$は狭義の単調増大(従って一対一)で、<br/> | ||
| + | $\quad$ $\lim_{\alpha \to \infty,\alpha \in {\bf Rat}}a^{\alpha} = \infty \quad \lim_{\alpha \to -\infty}f_a(\alpha) = 0 $ <br/> | ||
| + | $\quad$ 2)$a \lt 1$ のとき、 $f_a$は狭義の単調減少(従って一対一)で、<br/> | ||
| + | $\lim_{\alpha \to \infty,\alpha \in {\bf Rat}}f_a(\alpha) = 0\quad \lim_{\alpha \to -\infty,\alpha \in {\bf Rat}}f_a(\alpha) = \infty $ <br/> | ||
| + | $\quad$ 3)$a = 1$ のとき、$f_a \equiv 1$<br/><br/> | ||
| + | (3)関数 $f_a(\alpha) \triangleq a^{\alpha} \quad (\alpha \in {\bf Rat})$は連続関数である。<br/> | ||
| + | すなわち、<br/> | ||
| + | $\frac{m_k}{n_k}\to \frac{m}{n} \quad ({\bf N} \ni k\to \infty) \quad (m_k,m は整数、 n_k,n は自然数)$ <br/> | ||
| + | ならば、<br/> | ||
| + | $ a^{\frac{m_k}{n_k}} \to a^{\frac{m}{n}}$<br/><br/> | ||
| + | 証明<br/> | ||
| + | (1)、(2)はすでに証明したことなので、(3)だけを証明する。<br/> | ||
| + | $|a^{ \frac{m_k}{n_k} } - a^{ \frac{m}{n} }| = | ||
| + | |a^{ \frac{m}{n} }| |a^{ \frac{m_k}{n_k}- \frac{m}{n} }-1|$ なので、<br/> | ||
| + | $\lim_{\frac{m_k}{n_k}\to \frac{m}{n} }|a^{\frac{m_k}{n_k}- \frac{m}{n}}-1| = 0$<br/> | ||
| + | を、示せばよい。<br/> | ||
| + | $\frac{\tilde{m_k}}{\tilde{n_k}}\triangleq \frac{m_k}{n_k}- \frac{m}{n}$ とおくと、<br/> | ||
| + | $\lim_{ \frac{ \tilde{m_k} }{ \tilde{n_k} }\to 0 } | ||
| + | |a^{\frac{ \tilde{m_k} }{ \tilde{n_k} } } - 1|= 0$ <br/> | ||
| + | を示せばよい。<br/> | ||
| + | このために、次の補題をまず証明する。<br/> | ||
| + | '''補題'''<br/> | ||
| + | $\lim_{n\to \infty}|a^{ \frac{1}{n} }- 1|=0 \qquad \quad (b) $<br/> | ||
| + | $\lim_{n\to \infty}|a^{ \frac{-1}{n} }- 1|=0 \qquad \quad (c)$<br/> | ||
| + | 補題の証明<br/> | ||
| + | 1) 式(b)を背理法で証明する。<br/> | ||
| + | もし式(b)が成立しないとする。<br/> | ||
| + | すると或る小さな正数$\epsilon$ が存在し、<br/> | ||
| + | どのような自然数 $n_0$ をとっても、ある自然数$n \gt n_0$ が存在して<br/> | ||
| + | $|a^{ \frac{1}{n} }- 1| \geq \epsilon$<br/> | ||
| + | となる。(注参照)<br/> | ||
| + | すると、自然数の部分列 $\{ n_k \}_{k\in {\bf N}} | ||
| + | \quad (n_k \lt n_{k+1},k=1,2,3,\cdots)$ が存在して、<br/> | ||
| + | $(\forall k\in {\bf N})( |a^{ \frac{1}{n_k} }- 1| \geq \epsilon)\qquad (d)$<br/> | ||
| + | となる。<br/> | ||
| + | ① $a \gt 1$ の場合<br/> | ||
| + | $a^{ \frac{1}{n_k} } \gt 1$なので、<br/> | ||
| + | $(\forall k\in {\bf N})( a^{ \frac{1}{n_k} }- 1 \geq \epsilon)$<br/> | ||
| + | すなわち、<br/> | ||
| + | $(\forall k\in {\bf N})( a^{ \frac{1}{n_k} } \geq 1+\epsilon)$<br/> | ||
| + | 両辺を$n_k$乗して<br/> | ||
| + | $(\forall k\in {\bf N})(a \geq (1+\epsilon)^{n_k})$<br/> | ||
| + | 2項定理から<br/> | ||
| + | $(1+\epsilon)^{n_k} \geq 1+n_k\epsilon$ <br/> | ||
| + | であることがわかるので、<br/> | ||
| + | $(\forall k\in {\bf N})(a \geq 1+n_k\epsilon ) \qquad \qquad (e)$<br/> | ||
| + | $n_k \to \infty \quad (k \to \infty)$ なので、<br/> | ||
| + | 式(e)から、$a = \infty $ となり、矛盾が生じてしまう。<br/> | ||
| + | ② $a \lt 1$ の場合も同様にして、矛盾が生じることが示せる。<br/> | ||
| + | ③ 故に、式(b)が成立しないと仮定すると矛盾が生じるので、<br/> | ||
| + | 背理法により、式(b)が成立することが、証明できた。<br/> | ||
| + | 2)式(c)の証明も同様にしてできるので省略する。$\Box$<br/><br/> | ||
| + | 任意の正数$\epsilon$ に対して、ある番号$k_{\epsilon}$が定まって、<br/> | ||
| + | $k \geq k_{\epsilon}$というすべての自然数$k$に対して、<br/> | ||
| + | $|a^{\frac{ \tilde{m_k} }{ \tilde{n_k} } } - 1|\lt \epsilon$<br/> | ||
| + | を示せば、<br/> | ||
| + | $\lim_{ \frac{ \tilde{m_k} }{ \tilde{n_k} }\to 0 } | ||
| + | |a^{\frac{ \tilde{m_k} }{ \tilde{n_k} } } - 1|= 0$ <br/> | ||
| + | が示せて、証明が終了する。<br/> | ||
| + | 補題により、$\epsilon$ に対して、ある番号$n_0$をさだめ,<br/> | ||
| + | $n \geq n_0$ならば、<br/> | ||
| + | $|a^{ \frac{1}{n} }- 1|\lt \epsilon$<br/> | ||
| + | $|a^{ \frac{-1}{n} }- 1|\lt \epsilon$<br/> | ||
| + | が成立するようにできる。<br/> | ||
| + | $\lim_{k \to \infty}\frac{ \tilde{m_k} }{ \tilde{n_k} }= 0 $ | ||
| + | なので、<br/> | ||
| + | 自然数$n_0$に対して、 | ||
| + | ある番号$k(n)\in {\bf N}$ が存在して、<br/> | ||
| + | $k(n)$以上のどんな自然数$k$に対しても、<br/> | ||
| + | $\frac{-1}{n_0}\lt \frac{ \tilde{m_k} }{ \tilde{n_k}}\lt \frac{1}{n_0}$<br/> | ||
| + | すると指数関数$f_{a}(\alpha)=a^{\alpha}$ の単調性から、<br/> | ||
| + | $a^{ \frac{ \tilde{m_k} }{ \tilde{n_k} } }$ は、$a^{\frac{-1}{n_0}}$と$a^{\frac{-1}{n_0} }$の間の数となり、<br/> | ||
| + | $|a^{\frac{ \tilde{m_k} }{ \tilde{n_k} } } - 1|\lt \epsilon$<br/> | ||
| + | が示せた。<br/> | ||
| + | 定理の証明終わり。 $\qquad \qquad \qquad \qquad \Box$ | ||
==== 指数の実数への拡張 ==== | ==== 指数の実数への拡張 ==== | ||
| - | 任意の実数 $\alpha$ | + | $a$ を、正の実数とする。 |
| - | 定義<br/> | + | 任意の実数 $\alpha$ に対して 指数 $a^{\alpha}$ を定義しよう。<br/><br/> |
| - | $\{\alpha_n\}_{n=1}^{\infty}$ を $\alpha$ に収束する有理数の単調増加数列とするとき、<br/> | + | $\bf{定義}$<br/> |
| - | $a^{\alpha} \triangleq \lim_{n \to \infty}a^{\alpha_{n}}$ <br/> | + | 1)$\{\alpha_n\}_{n=1}^{\infty}$ を $\alpha$ に収束する有理数の単調増加数列とするとき、<br/> |
| - | + | $\underline{a^{\alpha}} \triangleq \lim_{n \to \infty}a^{\alpha_{n}}\qquad (a)$ <br/><br/> | |
| - | + | 2)$\{\beta_n\}_{n=1}^{\infty}$ を $\alpha$ に収束する有理数の単調減少数列とするとき、<br/> | |
| - | + | $\overline{a^{\alpha}} \triangleq \lim_{n \to \infty}a^{\beta_{n}}\qquad (b)$ <br/><br/> | |
| + | $\bf{命題6}$<br/> | ||
| + | 1)定義の式(a)、(b) は収束する。<br/> | ||
| + | 2)$\alpha$ に収束する、別の,<br/> | ||
| + | $\qquad$ 有理数の単調増加数列$\{\alpha'_n\}_{n=1}^{\infty}$と単調減少数列$\{\beta'_n\}_{n=1}^{\infty}$ をとっても、<br/> | ||
| + | $\qquad$ $\lim_{n \to \infty}a^{\alpha'_{n}} = \underline{a^{\alpha}} \qquad | ||
| + | \lim_{n \to \infty}a^{\beta'_{n}} = \overline{a^{\alpha}} $<br/> | ||
| + | 3)$\underline{a^{\alpha}} = \overline{a^{\alpha}} $<br/> | ||
証明<br/> | 証明<br/> | ||
| - | + | $a = 1$ の場合は 1の有理数乗は常に1になるので命題は明らかである。<br/> | |
| + | $a \gt 1$ の場合を証明する。$0 \lt a \lt 1$ の場合も同じように証明できる。<br/> | ||
| + | 1)${\bf Rat}$上の関数 $f_a(\alpha) = a^{\alpha}$ は単調増加(定理1)なので、<br/> | ||
| + | $\{a^{\alpha_{n}}\}_{n}$ は上に有界な単調増加数列、<br/> | ||
| + | $\{a^{\beta_{n}}\}_{n}$は下に有界な単調減少数列となる。<br/> | ||
| + | このため、「8.2 解析入門(1)」の | ||
| + | [[物理/解析入門(1)実数の性質、連続関数,微分と導関数#実数の連続性と極限#実数列の極限|「1.2.3 実数列の極限」]]の定理1から、<br/> | ||
| + | これらは、ともに収束することが保証される。<br/> | ||
| + | 2)$\lim_{n \to \infty}a^{\alpha'_{n}} =\lim_{n \to \infty}a^{\alpha_{n}}(= \underline{a^{\alpha}}) $を示そう。<br/> | ||
| + | $\gamma_{n}\triangleq \alpha_{n}-\alpha'_{n}\quad (\in \bf{Rat},n \in \bf{N})$ | ||
| + | とおく。<br/> | ||
| + | すると、$\lim_{n \to \infty}\gamma_{n}=0 \in \bf{Rat}$<br/> | ||
| + | 定理1(有理数を累乗とする指数関数の連続性)から、<br/> | ||
| + | $\lim_{n \to \infty}a^{\gamma_{n}}=a^0 = 1$<br/> | ||
| - | = | + | $a^{\gamma_{n}} |
| - | + | =a^{\alpha_{n}-\alpha'_{n}}$<br/> | |
| - | + | $=\frac{ a^{\alpha_{n}} }{ a^{\alpha'_{n}} } $ <br/> | |
| - | $ | + | 故に、<br/> |
| - | + | $\lim_{n \to \infty}\frac{ a^{\alpha_{n}} }{ a^{\alpha'_{n}} } = 1$ <br/> | |
| - | + | 上式の分子も分母も収束するので<br/> | |
| - | + | $1= \lim_{n \to \infty}\frac{a^{\alpha_{n}}}{ a^{\alpha'_{n}}}= | |
| - | + | \frac{ \lim_{n \to \infty}a^{\alpha_{n}} }{ \lim_{n \to \infty} a^{\alpha'_{n}} }$<br/> | |
| - | + | 3)2)の証明と殆ど同じようにして出来る。<br/> | |
| - | + | $\{\alpha_n\}_{n=1}^{\infty}$ を $\alpha$ に収束する有理数の単調増加数列<br/> | |
| - | $\ | + | $\{\beta_n\}_{n=1}^{\infty}$ を $\alpha$ に収束する有理数の単調減少数列とする。<br/> |
| - | $\ | + | $\gamma_{n}\triangleq \beta_{n}-\alpha_{n}\quad (\in \bf{Rat},n \in \bf{N})$ |
| - | $\ | + | とおく。<br/> |
| - | $\ | + | すると、$\lim_{n \to \infty}\gamma_{n}=0 \in \bf{Rat}$<br/> |
| - | $\ | + | 定理1(有理数を累乗とする指数関数の連続性)から、<br/> |
| - | + | $\lim_{n \to \infty}a^{\gamma_{n}}=a^0 = 1$<br/> | |
| - | + | $a^{\gamma_{n}} | |
| - | + | =a^{\beta_{n}-\alpha_{n}}$<br/> | |
| - | $ | + | $=\frac{ a^{\beta_{n}} }{ a^{\alpha_{n}} } $ <br/> |
| + | 故に、<br/> | ||
| + | $\lim_{n \to \infty}\frac{ a^{\beta_{n}} }{ a^{\alpha_{n}} } = 1$ <br/> | ||
| + | 上式の分子も分母も収束するので<br/> | ||
| + | $1= \lim_{n \to \infty}\frac{a^{\beta_{n}}}{ a^{\alpha_{n}}}= | ||
| + | \frac{ \lim_{n \to \infty}a^{\beta_{n}} }{ \lim_{n \to \infty} a^{\alpha_{n}} } = \frac{\overline{a^{\alpha}}}{\underline{a^{\alpha}}}$<br/> | ||
| + | 証明終わり。$\qquad \qquad \qquad \Box$ <br/><br/> | ||
| + | $\bf{a^{\alpha}の定義 }$<br/> | ||
| + | $a$ を任意の正の実数、$\alpha$ を任意の実数とするとき、<br/> | ||
| + | $a$ の $\alpha$乗を、<br/> | ||
| + | $a^{\alpha} \triangleq \underline{a^{\alpha}} (= \overline{a^{\alpha}})$<br/> | ||
| + | で定義する。<br/><br/> | ||
| + | |||
| + | |||
| + | $\Large{\bf{定理2}}$<br/> | ||
| + | 1)任意の正の実数$a$ に対して、その実数乗を上述のように定義すると、<br/> | ||
| + | 累乗の計算規則を満たす。<br/> | ||
| + | 2)実数空間 ${\bf R}$ で定義された指数関数<br/> | ||
| + | $f_{a}(x)= a^x \quad (x \in {\bf R})$ <br/> | ||
| + | は、$ a \neq 1$ ならば、一対一関数で<br/> | ||
| + | $ a \gt 1$ ならば単調増加、$\quad a \lt 1$ ならば単調減少である<br/> | ||
| + | 3)$ a \neq 1$ ならば、指数関数$f_{a}(x)= a^x$ は ${\bf R}$から無限開区間$(0,\infty)$の上への、連続関数である。<br/> | ||
証明<br/> | 証明<br/> | ||
| - | $\quad$ | + | 1)$ a, b $ を任意の正の実数、$\alpha,\quad \beta$を実数とすると、<br/> |
| - | $\quad$ | + | $a^{\alpha}a^{\beta} = a^{\alpha+\beta} \ (規則1)\quad |
| - | $\ | + | (a^{\alpha})^\beta =a^{\alpha \beta} \ (規則2)\quad (ab)^\beta = a^\beta b^\beta \ (規則3)$ を示せばよい。<br/> |
| - | $\ | + | 皆同じように証明できるので、規則1だけを証明する。<br/> |
| - | $\ | + | 実数 $\alpha$ に収束する任意の有理数の単調増加列 $\{\alpha_n\}_{n}$ と、<br/> |
| - | $\ | + | 実数 $\beta$ に収束する任意の有理数の単調増加列 $\{\beta_n\}_{n}$ をとれば、<br/> |
| - | $\quad | + | 定理1から、有理数乗では規則1は成り立つので、<br/> |
| - | $\quad$ (3) | + | $a^{\alpha_n}a^{\beta_n} = a^{\alpha_n+\beta_n} $<br/> |
| - | $\quad$ ( | + | 極限($\lim_{n\to \infty}$)をとれば、<br/> |
| - | $\quad$ | + | $\lim_{n\to \infty}(a^{\alpha_n}a^{\beta_n}) = \lim_{n\to \infty}a^{\alpha_n+\beta_n} $<br/> |
| - | $\quad$ | + | この左辺は極限の性質から$\lim_{n\to \infty}a^{\alpha_n}\lim_{n\to \infty}a^{\beta_n}$ に等しいので、<br/> |
| - | 証明終わり。<br/> | + | $\lim_{n\to \infty}a^{\alpha_n}\lim_{n\to \infty}a^{\beta_n}= \lim_{n\to \infty}a^{\alpha_n+\beta_n} \qquad \qquad (a)$<br/> |
| + | 命題6とその直後の$a^{\alpha}$の定義から、<br/> | ||
| + | $\lim_{n\to \infty}a^{\alpha_n} = \underline{a^{\alpha}}= a^{\alpha} $<br/> | ||
| + | $\lim_{n\to \infty}a^{\beta_n} = \underline{a^{\beta}}= a^{\beta} $<br/> | ||
| + | $\lim_{n\to \infty}a^{\alpha_n+\beta_n} = \underline{a^{\alpha+\beta}}= a^{\alpha + \beta} $<br/> | ||
| + | この3つの式を式(a)に代入すると、<br/> | ||
| + | $a^{\alpha}a^{\beta}=a^{\alpha + \beta} $<br/> | ||
| + | 累乗規則の1が成り立つことが示せた。<br/> | ||
| + | |||
| + | === 対数と対数関数 === | ||
| + | 1と異なる正の実数 $a$ を考える。<br/> | ||
| + | 指数関数 $f_{a}(x) = a^x$ は,定理2から、<br/> | ||
| + | ${\bf R}$ から $(0,\infty)$ の上への、一対一、連続関数である。<br/><br/> | ||
| + | 定義1<br/> | ||
| + | 実数 $a$ を $ a\gt 0,\ a\neq 1$ とする。この時、<br/> | ||
| + | 任意の正の実数 Xに対して、<br/> | ||
| + | $a^x = X$ <br/> | ||
| + | を満たす実数xが唯一つ定まる。<br/> | ||
| + | このxを X の'''$a$ を底とする対数'''と呼び、$\log_{a}X$ とかく。<br/><br/> | ||
| + | 指数関数 $f_{a}(x) = a^x$ は<br/> | ||
| + | ${\bf R}$ から $(0,\infty)$ の上への、一対一関数<br/> | ||
| + | なので、逆関数を考えることができる。<br/> | ||
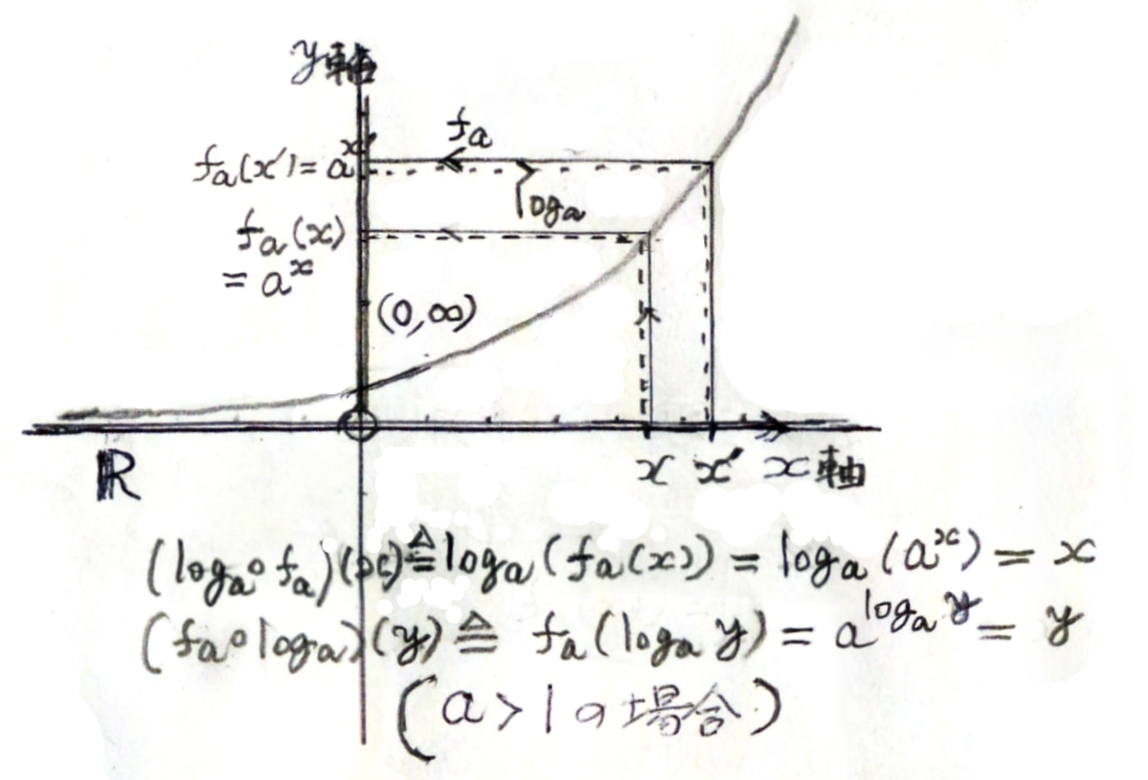
| + | *[[File:GENPHY00010804-01.pdf|right|frame|図 指数関数と対数関数]] | ||
| + | *[[File:図1 指数関数と対数関数.jpg]] | ||
| + | 定義2<br/> | ||
| + | $a$ を1と異なる正の実数とする。<br/> | ||
| + | $\log_{a} a^x \triangleq x \qquad \qquad \qquad (1)$ <br/> | ||
| + | この関数を、$a$ を底とする対数関数とよぶ。<br/><br/> | ||
| + | 定理1<br/> | ||
| + | $a$ を 1と異なる正の実数とする。<br/> | ||
| + | 1) $a$ を底とする対数関数 $\log_{a}$ は、<br/> | ||
| + | 指数関数$f_{a}(x)=a^x$の逆関数であり、<br/> | ||
| + | $(\log_{a}\cdot f_{a})(x) = x \quad (x \in {\bf R})\qquad \qquad \qquad (2) $ <br/> | ||
| + | すなわち、<br/> | ||
| + | $\log_{a}(a^x) = x \quad (x \in {\bf R})\qquad \qquad \qquad (2') $ <br/> | ||
| + | と(注参照)、<br/> | ||
| + | $(f_{a}\cdot \log_{a})(y) = y \quad \bigl(y \in (0,\infty)\bigr)\qquad \qquad \qquad (3) $ <br/> | ||
| + | すなわち、<br/> | ||
| + | $a^{\log_{a}(y)} = y \quad \bigl(y \in (0,\infty)\bigr)\qquad \qquad \qquad (3') $ <br/> | ||
| + | を満たす。<br/> | ||
| + | 2)指数関数$f_{a}(x)=a^x$ は <br/> | ||
| + | $(0,\infty)$ から ${\bf R}$ の上への一対一で<br/> | ||
| + | 連続な関数である。<br/> | ||
| + | (注) 2つの関数f、gに対して、その合成関数$(f\cdot g)$ は、<br/> | ||
| + | $(f\cdot g)(x)\triangleq f\bigl(g(x)\bigr)$ で定義される。<br/><br/> | ||
| + | |||
| + | 定理2<br/> | ||
| + | $a$ を 1と異なる正の実数とする。<br/> | ||
| + | すると<br/> | ||
| + | 1) 任意の2つの正の実数b、cに対して, <br/> | ||
| + | $\qquad \log_{a}b + \log_{a}c = \log_{a}bc \qquad \qquad \qquad (4)$<br/> | ||
| + | 2) 任意の2つの正の実数 b,c に対して,<br/> | ||
| + | $\qquad \log_{a}b - \log_{a}c = \log_{a}\frac{b}{c} \qquad \qquad \qquad (5)$<br/> | ||
| + | 3) 任意の正の実数 b と任意の実数 c に対して <br/> | ||
| + | $\qquad \log_{a}b^c = c \log_{a}b \qquad \qquad \qquad (6)$<br/> <br/> | ||
| + | 証明<br/> | ||
| + | 1) 指数関数$f_{a}(x)=a^x$ の性質から、<br/> | ||
| + | $a^{x_{b}}= b,\quad a^{x_{c}}= c \qquad \qquad \qquad (7)$ <br/> | ||
| + | を満たす、実数 $x_{b} \quad x_{c}$ がそれぞれ唯一つ定まる。<br/> | ||
| + | 式(7)から対数関数の定義を用いると、<br/> | ||
| + | $\log_{a}b = x_{b} \quad \log_{a}c = x_{c}\qquad \qquad \qquad (8)$ <br/> | ||
| + | すると、<br/> | ||
| + | $\quad \log_{a}b + \log_{a}c = x_b + x_c \quad (式(8)から)$<br/> | ||
| + | $=\log_{a} a^{x_b + x_c } \quad (式(1)から)$<br/> | ||
| + | $=\log_{a} (a^{x_b} a^{x_c }) \quad (指数関数の性質から)$<br/> | ||
| + | $=\log_{a}(bc) \quad (式(7)から) $<br/> <br/> | ||
| + | 2)も同様に証明できる。<br/> <br/> | ||
| + | 3)$X \triangleq \log_{a}b^c$ とおく。すると、対数の定義から、<br/> | ||
| + | $a^X = b^c$<br/> | ||
| + | $\qquad $ bは正の実数なので、$x_b=\log_{a}b とおくと、 a^{x_b}= b$なので、<br/> | ||
| + | $= (a^{x_b})^c = a^{x_b c} \quad (指数関数の性質から)$<br/> | ||
| + | 故に<br/> | ||
| + | $a^X = a^{x_b c}$<br/> | ||
| + | 指数関数が一対一関数なので、$X = x_b c = c \log_{a}b$<br/> | ||
| + | X の定義から、$\log_{a}b^c = c \log_{a}b \qquad \qquad \Box $<br/> <br/> | ||
| + | 定理3 底の変換公式<br/> | ||
| + | 任意の3つの正の実数 $a(\neq 1),b,c(\neq 1) $ に対して<br/> | ||
| + | $\qquad \log_{a}b = \frac{\log_{c}b}{\log_{c}a}\qquad \qquad \qquad (9)$<br/> <br/> | ||
| + | 証明<br/> | ||
| + | 定理1の式(3')から、<br/> | ||
| + | $ \quad a^{\log_{a}b} = b \qquad \qquad \qquad (10)$<br/> | ||
| + | 底をcとする対数をとれば、<br/> | ||
| + | $\log_{c}a^{\log_{a}b} = \log_{c} b$<br/> | ||
| + | $\qquad $定理2の式(6)から、$\log_{c}a^{\log_{a}b} = (\log_{a}b)(\log_{c}a)$なので、<br/> | ||
| + | $ (\log_{a}b)(\log_{c}a) = \log_{c} b$<br/> | ||
| + | $a,\quad c$ は、1と異なる正の実数であるため、$ \log_{c}a \neq 0$ となり、<br/>$\log_{a}b = \frac{\log_{c}b }{\log_{c}a}$<br/> | ||
| + | が得られた。<br/> | ||
| + | 証明終わり。 $\qquad \qquad \qquad \Box $<br/> | ||
=== 対数関数 === | === 対数関数 === | ||
1と異なる正の実数 $a$ を考える。<br/> | 1と異なる正の実数 $a$ を考える。<br/> | ||
| - | 指数関数 $f_{a}(x) = a^x$ は, | + | 指数関数 $f_{a}(x) = a^x$ は,定理2から、<br/> |
${\bf R}$ から $(0,\infty)$ の上への、一対一、連続関数である。<br/> | ${\bf R}$ から $(0,\infty)$ の上への、一対一、連続関数である。<br/> | ||
すると、その逆関数$\quad (0,\infty) \ni a^x \to x \in {\bf R} $ が定義できる。<br/> | すると、その逆関数$\quad (0,\infty) \ni a^x \to x \in {\bf R} $ が定義できる。<br/> | ||
| - | [[File:GENPHY00010804-01.pdf|right|frame|図 指数関数と対数関数]] | + | *[[File:GENPHY00010804-01.pdf|right|frame|図 指数関数と対数関数]] |
| + | *[[File:図1 指数関数と対数関数.jpg]] | ||
定義<br/> | 定義<br/> | ||
| 277 行: | 615 行: | ||
1) $a$ を底とする対数関数 $\log_{a}$ は、<br/> | 1) $a$ を底とする対数関数 $\log_{a}$ は、<br/> | ||
指数関数$f_{a}(x)=a^x$の逆関数であり、<br/> | 指数関数$f_{a}(x)=a^x$の逆関数であり、<br/> | ||
| - | $(\log_{a}\cdot f_{a})(x) = x \quad (x \in {\bf R})\qquad \qquad \qquad () $ <br/> | + | $(\log_{a}\cdot f_{a})(x) = x \quad (x \in {\bf R})\qquad \qquad \qquad (2) $ <br/> |
すなわち、<br/> | すなわち、<br/> | ||
| - | $\log_{a}(a^x) = x \quad (x \in {\bf R})\qquad \qquad \qquad () $ <br/> | + | $\log_{a}(a^x) = x \quad (x \in {\bf R})\qquad \qquad \qquad (2') $ <br/> |
と(注参照)、<br/> | と(注参照)、<br/> | ||
| - | $(f_{a}\cdot \log_{a})(y) = y \quad (y \in (0,\infty)\qquad \qquad \qquad () $ | + | $(f_{a}\cdot \log_{a})(y) = y \quad \bigl(y \in (0,\infty)\bigr)\qquad \qquad \qquad (3) $ <br/> |
すなわち、<br/> | すなわち、<br/> | ||
| - | $a^{\log_{a}(y)} = y \quad (y \in (0,\infty)\qquad \qquad \qquad () $ | + | $a^{\log_{a}(y)} = y \quad \bigl(y \in (0,\infty)\bigr)\qquad \qquad \qquad (3') $ <br/> |
を満たす。<br/> | を満たす。<br/> | ||
2)指数関数$f_{a}(x)=a^x$ は <br/> | 2)指数関数$f_{a}(x)=a^x$ は <br/> | ||
| 295 行: | 633 行: | ||
すると<br/> | すると<br/> | ||
1) 任意の2つの正の実数b、cに対して, <br/> | 1) 任意の2つの正の実数b、cに対して, <br/> | ||
| - | $\qquad \log_{a}b + \log_{a}c = \log_{a}bc \qquad \qquad \qquad ( | + | $\qquad \log_{a}b + \log_{a}c = \log_{a}bc \qquad \qquad \qquad (4)$<br/> |
2) 任意の2つの正の実数 b,c に対して,<br/> | 2) 任意の2つの正の実数 b,c に対して,<br/> | ||
| - | $\qquad \log_{a}b - \log_{a}c = \log_{a}\frac{b}{c} \qquad \qquad \qquad ( | + | $\qquad \log_{a}b - \log_{a}c = \log_{a}\frac{b}{c} \qquad \qquad \qquad (5)$<br/> |
3) 任意の正の実数 b と任意の実数 c に対して <br/> | 3) 任意の正の実数 b と任意の実数 c に対して <br/> | ||
| - | $\qquad \log_{a}b^c = c \log_{a}b \qquad \qquad \qquad ( | + | $\qquad \log_{a}b^c = c \log_{a}b \qquad \qquad \qquad (6)$<br/> <br/> |
証明<br/> | 証明<br/> | ||
| - | 1) 指数関数$f_{a}(x)=a^x$ の性質から、 | + | 1) 指数関数$f_{a}(x)=a^x$ の性質から、<br/> |
| - | + | $a^{x_{b}}= b,\quad a^{x_{c}}= c \qquad \qquad \qquad (7)$ <br/> | |
| + | を満たす、実数 $x_{b} \quad x_{c}$ がそれぞれ唯一つ定まる。<br/> | ||
| + | 式(7)から対数関数の定義を用いると、<br/> | ||
| + | $\log_{a}b = x_{b} \quad \log_{a}c = x_{c}\qquad \qquad \qquad (8)$ <br/> | ||
| + | すると、<br/> | ||
| + | $\quad \log_{a}b + \log_{a}c = x_b + x_c \quad (式(8)から)$<br/> | ||
| + | $=\log_{a} a^{x_b + x_c } \quad (式(1)から)$<br/> | ||
| + | $=\log_{a} (a^{x_b} a^{x_c }) \quad (指数関数の性質から)$<br/> | ||
| + | $=\log_{a}(bc) \quad (式(7)から) $<br/> <br/> | ||
| + | 2)も同様に証明できる。<br/> <br/> | ||
| + | 3)$X \triangleq \log_{a}b^c$ とおく。すると、対数の定義から、<br/> | ||
| + | $a^X = b^c$<br/> | ||
| + | $\qquad $ bは正の実数なので、$x_b=\log_{a}b とおくと、 a^{x_b}= b$なので、<br/> | ||
| + | $= (a^{x_b})^c = a^{x_b c} \quad (指数関数の性質から)$<br/> | ||
| + | 故に<br/> | ||
| + | $a^X = a^{x_b c}$<br/> | ||
| + | 指数関数が一対一関数なので、$X = x_b c = c \log_{a}b$<br/> | ||
| + | X の定義から、$\log_{a}b^c = c \log_{a}b \qquad \qquad \Box $<br/> <br/> | ||
定理3 底の変換公式<br/> | 定理3 底の変換公式<br/> | ||
| - | 任意の3つの正の実数 $a,b,c(\neq 1) $ に対して<br/> | + | 任意の3つの正の実数 $a(\neq 1),b,c(\neq 1) $ に対して<br/> |
| - | $\qquad \log_{a}b = \frac{\log_{c}b}{\log_{c}a}\qquad \qquad \qquad ( | + | $\qquad \log_{a}b = \frac{\log_{c}b}{\log_{c}a}\qquad \qquad \qquad (9)$<br/> <br/> |
| - | + | 証明<br/> | |
| - | + | 定理1の式(3')から、<br/> | |
| - | + | $ \quad a^{\log_{a}b} = b \qquad \qquad \qquad (10)$<br/> | |
| - | + | 底をcとする対数をとれば、<br/> | |
| - | + | $\log_{c}a^{\log_{a}b} = \log_{c} b$<br/> | |
| + | $\qquad $定理2の式(6)から、$\log_{c}a^{\log_{a}b} = (\log_{a}b)(\log_{c}a)$なので、<br/> | ||
| + | $ (\log_{a}b)(\log_{c}a) = \log_{c} b$<br/> | ||
| + | $a,\quad c$ は、1と異なる正の実数であるため、$ \log_{c}a \neq 0$ となり、<br/>$\log_{a}b = \frac{\log_{c}b }{\log_{c}a}$<br/> | ||
| + | が得られた。<br/> | ||
| + | 証明終わり。 $\qquad \qquad \qquad \Box $<br/> | ||
== 指数関数と対数関数の微分 == | == 指数関数と対数関数の微分 == | ||
2018年5月15日 (火) 05:01 時点における最新版
目次 |
「7.6 この章の付録」
問の解答
問
$\lim_{n\to \infty}(1+\frac{1}{n})^n$ が存在し、2より大きく3以下であることを証明する。
(1)準備; 2項定理を用いた展開
$a_n\triangleq (1+\frac{1}{n})^{n} \qquad (n は自然数)$ とおく。
すると、
$2 \leq a_1=1+\frac{1}{1}=2\quad \lt a_2=(1+\frac{1}{2})^{2} =2\frac{1}{4}$である。
以下に、数列 $\{a_n\}_{n=1}^{\infty}$ が単調増大で、有界(2より大、3より小)である事を示す。
するとテキストの定理により、この数列は2より大きく、3以下のある実数に収束することが分かる。
nが3以上の自然数の時は、$a_n$を2項定理を用いて展開すると
$a_n=(1+\frac{1}{n})^{n}=\sum_{m=0}^{n}{}_n\mathrm{C}_{m}1^{n-m}(\frac{1}{n})^m \qquad \qquad (1)$
ここで ${}_n\mathrm{C}_{m}$ は、n個のものからm個取り出す取り出し方の総数で、
mが1以上でn 以下の自然数の時は
${}_n\mathrm{C}_{m}=\frac{n!}{m!\ (n-m)!} \qquad \qquad (2)$
ここで、m が1以上の自然数の時は $ m!\triangleq 1\cdot 2\cdot 3 \cdots (m-1)\cdot m$
mが零の時は $\quad 0!\triangleq 1 $ と定義。
すると、
${}_n\mathrm{C}_{0}=\frac{n!}{0!\ n!}=1\qquad \qquad (3)$
$m \geq 1$のとき、${}_n\mathrm{C}_{m} =\frac{n!}{m!\ (n-m)!}=\frac{n\cdot (n-1)\cdot (n-2) \cdots \Bigl(n-(m-1)\Bigr) }{m!} \qquad (4)$
式(1)に式(2)を代入し,式(3)、(4)を利用して計算すると
$a_n = 1+\sum_{m=1}^{n}\frac{n(n-1)(n-2)\cdots \Bigl(n-(m-1)\Bigr)}{m!}1^{n-m}(\frac{1}{n})^m $
$=2+\sum_{m=2}^{n}\frac{1(1-\frac{1}{n})(1-\frac{2}{n})\cdots (1-\frac{m-1}{n})}{m!}\qquad \qquad (5)$
ここで、n より小さい全ての自然数 i に対して
$0 \lt 1-\frac{i}{n} \lt 1 $ なので、
$ 2 \lt a_n \lt 2+\sum_{m=2}^{n}\frac{1}{m!} \qquad \qquad \qquad (6)$
(2)すべての2以上の自然数 n に関して、
$ 2 \lt a_n \lt 3 \qquad \qquad \qquad (7)$
であることを示す。
式(6)から
$2\lt a_n$,
$a_n \lt 2+\sum_{m=2}^{n}\frac{1}{m!} \qquad \qquad (8)$
右辺の m は2以上の自然数なので、
$\frac{1}{m!} \leq \frac{1}{(m-1)m}=\frac{1}{m-1}-\frac{1}{m}$
である。故に、
$a_n \lt 2+\sum_{m=2}^{n}(\frac{1}{m-1}-\frac{1}{m})=2+(1-\frac{1}{n})=3-\frac{1}{n}\lt 3$
(3)数列 $\{a_n\}_{n=1}^{\infty}$ は単調増加
$n \geq 2$ の時、常に $a_n \lt a_{n+1}$ を示せばよい。
式(5)を利用すると(注参照)、
$a_{n+1}=2+\sum_{m=2}^{n+1}\frac{1(1-\frac{1}{n+1})(1-\frac{2}{n+1})\cdots (1-\frac{m-1}{n+1})}{m!}$
すると、
$a_{n+1} - a_n = \sum_{m=2}^{n+1}\frac{1(1-\frac{1}{n+1})(1-\frac{2}{n+1})\cdots (1-\frac{m-1}{n+1})}{m!} - \sum_{m=2}^{n}\frac{1(1-\frac{1}{n})(1-\frac{2}{n})\cdots (1-\frac{m-1}{n})}{m!} $
$\quad$ 右辺の第一項の和を2つに分けると、
$= \frac{1(1-\frac{1}{n+1})(1-\frac{2}{n+1})\cdots (1-\frac{n}{n+1})}{m!}$
$\quad + \sum_{m=2}^{n}\frac{1(1-\frac{1}{n+1})(1-\frac{2}{n+1})\cdots (1-\frac{m-1}{n+1})}{m!} - \sum_{m=2}^{n}\frac{1(1-\frac{1}{n})(1-\frac{2}{n})\cdots (1-\frac{m-1}{n})}{m!}$
$ = \frac{
1(1-\frac{1}{n+1})(1-\frac{2}{n+1})\cdots (1-\frac{n}{n+1})
}{m!}$
$\quad + \sum_{m=2}^{n}\frac{
1(1-\frac{1}{n+1})(1-\frac{2}{n+1})\cdots (1-\frac{m-1}{n+1})
-1(1-\frac{1}{n})(1-\frac{2}{n})\cdots (1-\frac{m-1}{n})}{m!}$
上の式で、全ての$i\in \{1,2,,,,n\}$に対して,$(1-\frac{i}{n+1})\gt 0$と$(1-\frac{i}{n+1})\gt (1-\frac{i}{n})$ なので、
$a_{n+1} - a_n \gt 0$
(注)式(3)のnに n+1 を代入すればよい。
ネイピア数 e について
定義;$e\triangleq \lim_{}(1+\frac{1}{n})^n$ をネイピア数と呼ぶ。
命題1
(1)$ 2 \lt e \leq 3$
(2)$e=\sum_{m=0}^{\infty}\frac{1}{m!} \qquad ただし、0!\triangleq 1,\quad m!\triangleq 1\cdot 2\cdot 3\cdots (m-1)\cdot m \qquad \qquad (9)$
三角関数の微分
準備
次の命題が、三角関数の微分を求めるうえで中心的役割を果たす。
命題2
$\lim_{\theta\to 0,\theta\neq 0}\frac{\sin \theta}{\theta}=1$
証明
まず、$\theta$ を正に保ちながら零に近づける場合を考える。
すると、$ 0 \lt \theta \lt \pi/2 $ と考えて良い。
点Oを中心にし、半径1の円を考え、円周上に一点Aをさだめる。
図のように、円周上の点Bを、線分OBが直線OAとなす角がx(ラジアン)となるようにとる。
図から$\triangle{OAB} \subset 扇形OAB \subset \triangle{OAP} $
$\quad$ ここで、点PはAを通り線分OAと垂直な直線と半直線OBの交点。
すると、
$\triangle{OAB}の面積 \lt 扇形OAB の面積 \lt \triangle{OAP}の面積$
ここで、$\triangle{OAB}の面積=\frac{1\cdot \sin{\theta}}{2},\quad 扇形OAB の面積=\pi\cdot 1^{2}\cdot \frac{\theta}{2\pi}\quad \triangle{OAP}の面積=\frac{1\cdot \tan{\theta}}{2}$なので、
$\frac{\sin{\theta}}{2} \lt \frac{\theta}{2}\lt \frac{\tan{\theta}}{2}=\frac{\sin{\theta}}{2\cos{\theta}}\qquad $各項を2倍すると、
$\sin{\theta}\lt \theta \lt \frac{\sin{\theta}}{\cos{\theta}}$
$\quad$ここで $\sin{\theta}\gt 0$ なので、これで上式の各項を割ると、
$1 \lt \frac{\theta}{\sin{\theta}} \lt \frac{1}{\cos{\theta}}$
$1 \gt \frac{\sin{\theta}}{\theta} \gt \cos{\theta}$
故に、極限の性質から
$1 \geq \lim_{\theta\to 0,\theta\neq 0}\frac{\sin \theta}{\theta} \geq \lim_{\theta\to 0,\theta\neq 0}\cos{\theta}=1$
これより、$\lim_{\theta\to 0,\theta\neq 0}\frac{\sin \theta}{\theta}=1$ が得られる。
定理1 三角関数の微分
(1)$\frac{d}{d\theta}\sin{\theta}=\cos{\theta}$
(2)$\frac{d}{d\theta}\cos{\theta}=-\sin{\theta}$
証明
(1); $\frac{d}{d\theta}\sin{\theta} \triangleq \lim_{h\to 0,h\neq 0}\frac{\sin (\theta+h)-\sin \theta}{h}$
ここで、
$\sin (\theta+h)-\sin \theta = \sin \bigl((\theta + \frac{h}{2})+\frac{h}{2}\bigr) - \sin \bigl((\theta + \frac{h}{2})-\frac{h}{2}\bigr)$
サイン関数の加法定理を適用すると
$=\sin (\theta + \frac{h}{2})\cos \frac{h}{2} + \cos (\theta + \frac{h}{2})\sin \frac{h}{2} - \Bigl( \sin (\theta + \frac{h}{2})\cos \frac{h}{2} - \cos (\theta + \frac{h}{2})\sin \frac{h}{2} \Bigr) = 2\cdot \cos (\theta + \frac{h}{2})\sin \frac{h}{2}$
故に、
$\frac{d}{d\theta}\sin{\theta} \triangleq \lim_{h\to 0,h\neq 0}\frac{\sin (\theta+h)-\sin \theta}{h} = \lim_{h\to 0,h\neq 0}\frac{2\cdot \cos (\theta + \frac{h}{2})\sin \frac{h}{2}}{h}=\lim_{h\to 0,h\neq 0}\cos (\theta + \frac{h}{2})\frac{\sin \frac{h}{2}}{h/2}$
$=\lim_{h\to 0,h\neq 0}\cos (\theta + \frac{h}{2})\lim_{h\to 0,h\neq 0}\frac{\sin \frac{h}{2}}{h/2}$
$\quad $ ここで、
$\quad \lim_{h\to 0,h\neq 0}\cos (\theta + \frac{h}{2}) = \cos \theta$
$\quad \lim_{h\to 0,h\neq 0}\frac{\sin \frac{h}{2}}{h/2} = 1 \quad (上の命題2より)$
$\quad $なので、
$=\cos \theta$
指数関数と対数関数
正の実数の累乗の指数の拡張
実数の累乗(自然数乗)
$a$ を任意の実数、$n$ を2以上の自然数とする。
$a^1=a,\quad a^2=a\cdot a,\quad a^3=a^2\cdot a=a\cdot a\cdot a ,\quad \cdots \quad a^n=a^{n-1}\cdot a, \cdots$
を総称して、a の累乗と呼ぶ。
$a^n$ を$a $ の n 乗 、$n$ をその指数と呼ぶ。
実数の自然数乗の3つの計算規則
累乗が次のような計算規則を満たすことは、容易に証明できる。
命題3
$ a,b $ を任意の実数、$ m, n $ を任意の自然数とすると、
(1) $a^{m}a^{n} = a^{m+n} $
(2) $(a^{m})^n =a^{m n} $
(3) $(ab)^n = a^n b^n $
証明は、累乗の定義と積の交換法則から容易にできるので省略する。
指数関数とn次関数
$a$ を正の実数とするとき、累乗$a^{\alpha}$ の
$\alpha$ を独立変数とするか、$a$ を独立変数にするかで、
次の2種の関数が定まる。
定義
$a$ を正の実数, $\alpha$を自然数とするとき、次の2つの関数を考える。
1)$f_{a}; ({\bf N} \ni) \alpha \to a^{\alpha} \bigl(\in {\bf R}^{+}\triangleq (0,\infty)\bigr)$
これは、指数を変数とする関数なので、指数関数という。
2)$g_{\alpha}; ({\bf R}^{+}\ni) a \to a^{\alpha} (\in {\bf R}^{+})$
これは、$\alpha$次の単項関数である。
命題 指数関数の性質
指数関数$f_{a}(\alpha )=a^{\alpha} \quad (\alpha \in {\bf N})$ は次の性質を持つ。
1)$0 \lt a \lt 1$のとき、${\bf N}$から${\bf R}^{+}$への狭義単調減少の連続関数で、$\lim_{\alpha \to \infty ,\alpha \in {\bf N} } a^{\alpha} = 0$
2)$1 \lt a$のとき、${\bf N}$から${\bf R}^{+}$への狭義単調増加の連続関数
で、
$\lim_{\alpha \to \infty ,\alpha \in {\bf N} } a^{\alpha} = \infty$
連続性以外は、明らかなので証明は省略する。
自然数全体の集合${\bf N}$は離散集合なので、
そのうえで定義された任意の関数は連続となる。
「8.2 解析入門(1)実数の性質、連続関数、微分 $\quad$ 「1.3 関数とその連続性」の「1.3.2 関数の極限と連続性」を参照のこと。
命題 $n$次の単項関数の性質
$\alpha= n \in {\bf N}$ とする。
$n$次の単項関数$g_{n}(a)=a^{n} \quad (a \in {\bf R}^{+})$ は
${\bf R}^{+}$から${\bf R}^{+}$への狭義単調増加の連続関数で、
$\lim_{a\to 0,a \in {\bf R}^{+} } a^{n} = 0$
$\lim_{a\to \infty,a\in {\bf R}^{+} } a^{n} = \infty$
である。
証明
${\bf R}^{+}$上では狭義単調増加であることは容易に示せる。
連続性については、$\lim_{\delta \to 0}(a+\delta)^n = a^n $ であることを示せばよい。
例えば、2項定理で$(a+\delta)^n $ を展開して極限をとればよい。
この節の目的
この節の目的は、累乗にかんする計算規則を満たすようにしながら、
累乗の指数を実数まで拡張することである。
しかし $a$ が負数だと、指数を有理数に拡張するとき不都合が起きてしまう。
例えば
$\frac{1}{2}$ の時, $a^{\frac{1}{2}}= \sqrt{a}$ は実数でなく虚数となり、
実数値関数の枠組みに収まらなくなる。
そこで、このような不都合が起こらないように 今後は$a$ を正の実数に限定し、
次の計算規則を満たすようにしながら、指数を自然数から整数、整数から有理数、有理数から実数へと順に拡張していく。
累乗に関する計算規則
$ a, b $ を任意の正の実数、$\alpha,\quad \beta$を指数とすると、
(1) $a^{\alpha}a^{\beta} = a^{\alpha+\beta} \qquad \qquad \qquad (累乗規則1)$
(2) $(a^{\alpha})^\beta =a^{\alpha \beta} \qquad \qquad \qquad (累乗規則2)$
(3) $(ab)^\beta = a^\beta b^\beta \qquad \qquad \qquad (累乗規則3)$
計算規則(3)を守ろうとすると、$1^\beta \equiv 1$ と定めなければならないことが分かる。
何故ならば $b=1$の時、$a^\beta = (a・1)^\beta = a^\beta 1^\beta $ となり、 $a^\beta \neq 0$ であるから。
そこで 今後は常に $1^\beta \equiv 1$ と定め、 $a \neq 1$ の場合だけを考察する。
本節のもう一つの目的は、指数の拡張に伴い累乗に伴う2つの関数
$f_{a}(\alpha)=a^\alpha$ と$g_{\alpha}(a)=a^\alpha$ の性質が、どのようになるか考察する事である。
指数の整数への拡張
任意の正の実数$a(\neq 0,1)$ を考える。
$a$の累乗の指数を、累乗に関する3つの規則が成り立つようにしながら、整数に拡張しよう。
まず、規則(1)を守ろうとすれば
$a^0 = 1 \qquad \qquad \qquad (4) $
と定義しなければならないことが分かる。
何故ならば、$n\in {\bf N}$ の時、
$a^{n} = a^{n+0}= a^n a^0 $
となり、 $a^n \neq 0$ だから両辺を $a^n$ で割ればよい。
次に任意の自然数 n に対して、
$a^{-n}$ を累乗に関する規則(1)を満たすように定義しよう。
$a^{-n}a^n = a^{-n+n} = a^0 = 1$
両辺を $a^n$ で割れば
$a^{-n} = \frac{1}{a^n} \qquad \qquad \qquad(5)$
命題
式(4),(5)に従って指数を整数に拡大すると、
3つの累乗の規則はすべて成立する。
証明
指数が負のときは式(5)を用いて、指数が自然数の式に書き直し、
指数が自然数のときに成り立つことが分かっている3つの計算規則を使って式の変形をすれば良い。
計算規則の(1)の証明だけを示そう。
(1)$\alpha ,\beta $ を任意の整数とすると、
$ a^{\alpha}a^{\beta} = a^{(\alpha +\beta) }$ であることを示す。
(ケース1)指数の一方が正の整数(自然数)で、他方が負の整数の時
$m,n$ を自然数として、
$ a^{m}a^{-n} = a^{m-n}$ を示せばよい。
式(5)から
$ a^{m}a^{-n} = \frac{a^m}{a^n} \qquad \qquad \qquad (6)$
$m \gt n$ 、$m=n$ 、$m \lt n$ という3つの場合に分けて証明する。
1)$m \gt n$ の時
割り算を実行すると$\frac{a^m}{a^n}=a^{m-n} $
この式と、式(6)から、$ a^{m}a^{-n} = a^{m-n} $
2) $m=n$ の時
$\frac{a^m}{a^n}= 1 = a^{m-n} $
この式と、式(6)から、$ a^{m}a^{-n} = a^{m-n} $
3) $m \lt n$ の時
割り算を実行すると、
$\frac{a^m}{a^n}= \frac{1}{a^{(n-m)}}$
$=a^{m-n} $
(ケース2)両方の指数が負の整数の時
$a^{-m}a^{-n} = a^{-m-n}$ を示せばよい。
$a^{-m}a^{-n} = \frac{1}{a^m}\frac{1}{a^n}=\frac{1}{a^m a^n}=\frac{1}{a^{(m+n)}}
=a^{-m-n}$
指数の有理数への拡張
これ以降、有理数全体のなす集合を${\bf Rat}$とかく。
$ a (\neq 1)$ を任意の正の実数、 $\frac{m}{n}$ を任意の有理数のとき、
$ a $ の有理数乗 $a^{\frac{m}{n}}$ を、計算規則を満たすように定義しよう。
指数n を任意の自然数(正の整数)、 m を任意の整数と仮定してよい。
$\qquad $(注)nが負の時は$a^{\frac{m}{n}} = a^{\frac{-m}{-n}}$ なので、
$\qquad \quad -n,-m $を改めて$n,m$ と置けば良い。$\Box$
累乗規則(2)を満たすように定義するには、
$(a^{\frac{m}{n}})^{n} = (a^{\frac{m}{n}})^{\frac{n}{1}} = a^{m}$
でなければならない。
これは、$a^{\frac{m}{n}}$ が $a^{m}$ のn乗根であることを示す。
しかしnが偶数のときは、$-a^{\frac{m}{n}}$ も$a^{m}$ のn乗根となるので、
正のn乗根 のほうを、$a^{\frac{m}{n}}$ とかく。
定義 正の実数の有理数乗
$a$を正の実数とする。
$a^{\frac{m}{n}}$ とは、
$a^{m}$ の正のn乗根である。
すなわち、
$(a^{\frac{m}{n}})^{n} =a^{m} $を満たす正の実数である。
最初に、この定義できちんと正の実数が一つだけ決まることを証明しよう。
$a=1$のときは、n乗すると1になる正数は1だけなので
$1^{\frac{m}{n}}=1 $
であることが分かるので、$a \neq 1$ の場合を考える。
命題3
$a \neq 0,1$ を任意の正の実数、$ m$ を任意の整数,$n$を任意の自然数とする。
すると、n 乗すると $a^{m}$ になる正の実数 $ b $ (i.e. $\quad b^n = a^{m}$)が存在し、ただ一つに限る。
証明
(1) 存在性
$ f(x) \triangleq x^n $ という、零と正の実数の上で定義された、関数を考える。
この関数はxが増加するにつれて、連続的に、零から正の無限大に狭義に単調に増加(注参照)していく。
そこで、$B\triangleq \{x \in [0,\infty)\ |\ x^n \leq a^{m} \}$ という集合を考える。
この集合は、上に有界な区間になり、実数の連続性から上限(sup)$b$を持つ。
この時、$ b \in B, \quad b^n = a^{m}$ であることを示そう。
$b$ が集合$B (\in {\bf R})$の上限なので、任意の自然数nに対して、
$0 \leq b - b_{n} \lt \frac{1}{n} $
を満たす $ b_{n} \in B $ が存在する。
明らかに
$ \lim_{n \to \infty}b_{n} = b $
すると、関数 $ f(x) \triangleq x^n $ は連続なので、
$ \lim_{n \to \infty}b_{n}^n = b^n \qquad \qquad \qquad (a)$
ところが$ b_{n} \in B \triangleq \{x \in [0,\infty)|x^n \leq a^{m} \}$なので、
$ b_{n}^n \leq a^{m} \qquad \qquad \qquad (b)$
式(a)、(b) から、$ b^n \leq a^{m}$ がえられるので、
$ b \in B$
が示せた。(従って、Bは閉区間 [o,b] である。)
$b^n = a^{m}$ であることを背理法を使って示そう。
もし、$b^n \lt a^{m}$ だとすると、関数 $ f(x) = x^n $ は連続なので
充分小さな正の実数$\delta$ をとると、$(b + \delta) ^n \lt a^{m}$ を満たす。
すると $(b + \delta) \in B$ となり、
$b$が B の上限であることに矛盾してしまう。
故に、背理法により、$b^n = a^{m} $ が証明できた。
(2)一意性
関数 $ f(x) = x^n $ は狭義の単調増加関数なのでb以外の数b'($\neq b$)では、
${b'}^n \neq b^n =a^m$
(証明終り) $ \qquad \qquad \Box$
(注) 関数fが狭義単調増加とは、$ x \lt y \Rightarrow f(x) \lt f(y) $ を満たすこと。
命題4
任意の正の実数 $a \neq 1$ にたいして、その有理数乗を上記のように定義すると
3つの累乗規則 (1)~(3) が成り立つ。
証明;
1) 累乗規則(1)が成り立つことを示す。
2個の有理数の指数を 自然数$n,\quad \tilde{n}$と整数$m,\quad \tilde{m}$ を用いて、
$\alpha = \frac{m}{n},\quad \beta = \frac{\tilde{m}}{\tilde{n}}$と表現する。
すると、累乗規則(1)は、次のように表される。
$a^{\frac{m}{n}}a^{\frac{\tilde{m}}{\tilde{n}}} = a^{\frac{m}{n}+\frac{\tilde{m}}{\tilde{n}}} $
この左辺を $b \triangleq a^{\frac{m}{n}}a^{\frac{\tilde{m}}{\tilde{n}}}$,
右辺を $c \triangleq a^{\frac{m}{n}+\frac{\tilde{m}}{\tilde{n}}}$ とおく。
$b^{n \tilde{n}} = c^{n \tilde{n}} \qquad \qquad \qquad (a)$
であることを示せば、$b = c$ が得られ,
累乗規則(1)が成立することが分かる。
まず左辺を考える。
$b^{n \tilde{n}} = (a^{\frac{m}{n}}a^{\frac{\tilde{m}}{\tilde{n}}})^{n \tilde{n}}$
指数が自然数の累乗規則(3)から
$ = (a^{\frac{m}{n}})^{n \tilde{n}}(a^{\frac{\tilde{m}}{\tilde{n}}})^{n \tilde{n}}$
指数が自然数の累乗規則(2)から
$= \Bigl((a^{\frac{m}{n}})^{n}\Bigr)^{\tilde{n}}\Bigl((a^{\frac{\tilde{m}}{\tilde{n}}})^{\tilde{n}}\Bigr)^{n}$
実数の有理数乗の定義から、
$ = (a^{m})^{\tilde{n}}(a^{\tilde{m}})^{n}$
指数が整数の累乗規則(2)から
$ = a^{m \tilde{n}}a^{\tilde{m}n}$
指数が整数の累乗規則(1)から
$ = a^{m \tilde{n} + \tilde{m}n}$
故に、$b^{n \tilde{n}} = a^{m \tilde{n} + \tilde{m}n}$
次に、右辺を考える。
$c^{n \tilde{n}} = (a^{\frac{m}{n}+\frac{\tilde{m}}{\tilde{n}}})^{n \tilde{n}}$
$ = (a^{ \frac{m\tilde{n}+n\tilde{m}}{n\tilde{n}}})^{n \tilde{n}}$
実数の有理数乗の定義から、
$ = a^{m\tilde{n} + n\tilde{m}} = b^{n \tilde{n}}$
これで、式(a)が示され、累乗規則(1)が成り立つことが証明できた。
2)累乗規則(2)と累乗規則(3)が成り立つことは読者がしてください。
証明終わり。
指数が有理数の場合,命題2は次のように拡張出来る。
命題5
${\bf Rat}$の上で定義される関数
$f_a(\alpha) \triangleq a^{\alpha} \qquad (\alpha \in {\bf Rat})$を考える。
1)$a$ を1より大きい正の実数とすると、
$f_a$は単調増大で
$\lim_{\alpha \to \infty,\alpha \in {\bf Rat}}a^{\alpha} = \infty \quad \lim_{\alpha \to -\infty}f_a(\alpha) = 0 $
2)$a$ が1より小さい正の実数のとき、
$f_a$は単調減少し、
$\lim_{\alpha \to \infty,\alpha \in {\bf Rat}}f_a(\alpha) = 0\quad \lim_{\alpha \to -\infty,\alpha \in {\bf Rat}}f_a(\alpha) = \infty $
3)$a = 1$ のとき、$f_a \equiv 1$
証明
1)のみ証明する。2)の場合も同様に証明できる。
① $\frac{m}{n} \lt \frac{m'}{n'} ,\quad n,m \in {\bf N} $ とすると、
$a^{\frac{m}{n}} \lt a^{\frac{m'}{n'}}$ を示そう。
$\alpha \triangleq a^{\frac{m'}{n'}} \div a^{\frac{m}{n}} \gt 1$
を示せばよい。
正数の有理数乗の計算規則から、
$\alpha \triangleq a^{\frac{m'}{n'}} \div a^{\frac{m}{n}}=a^{\frac{m'}{n'}-\frac{m}{n}}$
$=a^{ \frac{m'n-n'm}{n'n} }$
故に、
${\alpha}^{n'n} = a^{m'n-n'm}$
$\qquad \frac{m}{n} \lt \frac{m'}{n'}$ から、
$\qquad m'n-n'm \gt 0 $なので、$a^{m'n-n'm} \gt 1$であり
$ \gt 1$
故に、 ${\alpha}^{n'n} \gt 1$
自然数乗すると1より大きくなる正の実数は1より大きい実数しかないので、
$\alpha \gt 1$ が得られた。
② $\lim_{\alpha \to \infty,\alpha \in {\bf Rat}}a^{\alpha}= \infty $を示そう。
関数 $f_a(\alpha)$ は単調増加(①で証明)なので、
$\lim_{n \to \infty,n \in {\bf N}}a^n = \infty $
を示せばよいが、これは自明である。
③ $\lim_{\alpha \to -\infty,\alpha \in {\bf Rat}}f_a(\alpha) = 0 $
も、同様にして示せる。
証明終わり $\qquad \qquad \qquad \Box$
以上の結果をまとめて、次の定理を得る。
$\Large {\bf{定理1}}$
$a \neq 0,1$ の正の実数とする。
(1)$ a $ の有理数乗 $a^{\frac{m}{n}}\quad(m;整数、n \in {\bf N})$ を$a^{m}$の正の$n$乗根で定義すると、
累乗に関する計算規則
$ a, b $ を任意の正の実数、$\alpha,\beta \in {\bf Rat} $を指数とすると、
$\quad$ 1) $a^{\alpha}a^{\beta} = a^{\alpha+\beta} \qquad \qquad (累乗規則1)$
$\quad$ 2) $(a^{\alpha})^\beta =a^{\alpha \beta} \qquad \qquad (累乗規則2)$
$\quad$ 3) $(ab)^\beta = a^\beta b^\beta \qquad \qquad (累乗規則3)$
を満たす。
(2)${\bf Rat}$の上で定義される関数
$f_a(\alpha) \triangleq a^{\alpha} \qquad (\alpha \in {\bf Rat})$を考えると、
$\quad$1)$a\gt 1$ のとき、 $f_a$は狭義の単調増大(従って一対一)で、
$\quad$ $\lim_{\alpha \to \infty,\alpha \in {\bf Rat}}a^{\alpha} = \infty \quad \lim_{\alpha \to -\infty}f_a(\alpha) = 0 $
$\quad$ 2)$a \lt 1$ のとき、 $f_a$は狭義の単調減少(従って一対一)で、
$\lim_{\alpha \to \infty,\alpha \in {\bf Rat}}f_a(\alpha) = 0\quad \lim_{\alpha \to -\infty,\alpha \in {\bf Rat}}f_a(\alpha) = \infty $
$\quad$ 3)$a = 1$ のとき、$f_a \equiv 1$
(3)関数 $f_a(\alpha) \triangleq a^{\alpha} \quad (\alpha \in {\bf Rat})$は連続関数である。
すなわち、
$\frac{m_k}{n_k}\to \frac{m}{n} \quad ({\bf N} \ni k\to \infty) \quad (m_k,m は整数、 n_k,n は自然数)$
ならば、
$ a^{\frac{m_k}{n_k}} \to a^{\frac{m}{n}}$
証明
(1)、(2)はすでに証明したことなので、(3)だけを証明する。
$|a^{ \frac{m_k}{n_k} } - a^{ \frac{m}{n} }| =
|a^{ \frac{m}{n} }| |a^{ \frac{m_k}{n_k}- \frac{m}{n} }-1|$ なので、
$\lim_{\frac{m_k}{n_k}\to \frac{m}{n} }|a^{\frac{m_k}{n_k}- \frac{m}{n}}-1| = 0$
を、示せばよい。
$\frac{\tilde{m_k}}{\tilde{n_k}}\triangleq \frac{m_k}{n_k}- \frac{m}{n}$ とおくと、
$\lim_{ \frac{ \tilde{m_k} }{ \tilde{n_k} }\to 0 }
|a^{\frac{ \tilde{m_k} }{ \tilde{n_k} } } - 1|= 0$
を示せばよい。
このために、次の補題をまず証明する。
補題
$\lim_{n\to \infty}|a^{ \frac{1}{n} }- 1|=0 \qquad \quad (b) $
$\lim_{n\to \infty}|a^{ \frac{-1}{n} }- 1|=0 \qquad \quad (c)$
補題の証明
1) 式(b)を背理法で証明する。
もし式(b)が成立しないとする。
すると或る小さな正数$\epsilon$ が存在し、
どのような自然数 $n_0$ をとっても、ある自然数$n \gt n_0$ が存在して
$|a^{ \frac{1}{n} }- 1| \geq \epsilon$
となる。(注参照)
すると、自然数の部分列 $\{ n_k \}_{k\in {\bf N}}
\quad (n_k \lt n_{k+1},k=1,2,3,\cdots)$ が存在して、
$(\forall k\in {\bf N})( |a^{ \frac{1}{n_k} }- 1| \geq \epsilon)\qquad (d)$
となる。
① $a \gt 1$ の場合
$a^{ \frac{1}{n_k} } \gt 1$なので、
$(\forall k\in {\bf N})( a^{ \frac{1}{n_k} }- 1 \geq \epsilon)$
すなわち、
$(\forall k\in {\bf N})( a^{ \frac{1}{n_k} } \geq 1+\epsilon)$
両辺を$n_k$乗して
$(\forall k\in {\bf N})(a \geq (1+\epsilon)^{n_k})$
2項定理から
$(1+\epsilon)^{n_k} \geq 1+n_k\epsilon$
であることがわかるので、
$(\forall k\in {\bf N})(a \geq 1+n_k\epsilon ) \qquad \qquad (e)$
$n_k \to \infty \quad (k \to \infty)$ なので、
式(e)から、$a = \infty $ となり、矛盾が生じてしまう。
② $a \lt 1$ の場合も同様にして、矛盾が生じることが示せる。
③ 故に、式(b)が成立しないと仮定すると矛盾が生じるので、
背理法により、式(b)が成立することが、証明できた。
2)式(c)の証明も同様にしてできるので省略する。$\Box$
任意の正数$\epsilon$ に対して、ある番号$k_{\epsilon}$が定まって、
$k \geq k_{\epsilon}$というすべての自然数$k$に対して、
$|a^{\frac{ \tilde{m_k} }{ \tilde{n_k} } } - 1|\lt \epsilon$
を示せば、
$\lim_{ \frac{ \tilde{m_k} }{ \tilde{n_k} }\to 0 }
|a^{\frac{ \tilde{m_k} }{ \tilde{n_k} } } - 1|= 0$
が示せて、証明が終了する。
補題により、$\epsilon$ に対して、ある番号$n_0$をさだめ,
$n \geq n_0$ならば、
$|a^{ \frac{1}{n} }- 1|\lt \epsilon$
$|a^{ \frac{-1}{n} }- 1|\lt \epsilon$
が成立するようにできる。
$\lim_{k \to \infty}\frac{ \tilde{m_k} }{ \tilde{n_k} }= 0 $
なので、
自然数$n_0$に対して、
ある番号$k(n)\in {\bf N}$ が存在して、
$k(n)$以上のどんな自然数$k$に対しても、
$\frac{-1}{n_0}\lt \frac{ \tilde{m_k} }{ \tilde{n_k}}\lt \frac{1}{n_0}$
すると指数関数$f_{a}(\alpha)=a^{\alpha}$ の単調性から、
$a^{ \frac{ \tilde{m_k} }{ \tilde{n_k} } }$ は、$a^{\frac{-1}{n_0}}$と$a^{\frac{-1}{n_0} }$の間の数となり、
$|a^{\frac{ \tilde{m_k} }{ \tilde{n_k} } } - 1|\lt \epsilon$
が示せた。
定理の証明終わり。 $\qquad \qquad \qquad \qquad \Box$
指数の実数への拡張
$a$ を、正の実数とする。
任意の実数 $\alpha$ に対して 指数 $a^{\alpha}$ を定義しよう。
$\bf{定義}$
1)$\{\alpha_n\}_{n=1}^{\infty}$ を $\alpha$ に収束する有理数の単調増加数列とするとき、
$\underline{a^{\alpha}} \triangleq \lim_{n \to \infty}a^{\alpha_{n}}\qquad (a)$
2)$\{\beta_n\}_{n=1}^{\infty}$ を $\alpha$ に収束する有理数の単調減少数列とするとき、
$\overline{a^{\alpha}} \triangleq \lim_{n \to \infty}a^{\beta_{n}}\qquad (b)$
$\bf{命題6}$
1)定義の式(a)、(b) は収束する。
2)$\alpha$ に収束する、別の,
$\qquad$ 有理数の単調増加数列$\{\alpha'_n\}_{n=1}^{\infty}$と単調減少数列$\{\beta'_n\}_{n=1}^{\infty}$ をとっても、
$\qquad$ $\lim_{n \to \infty}a^{\alpha'_{n}} = \underline{a^{\alpha}} \qquad
\lim_{n \to \infty}a^{\beta'_{n}} = \overline{a^{\alpha}} $
3)$\underline{a^{\alpha}} = \overline{a^{\alpha}} $
証明
$a = 1$ の場合は 1の有理数乗は常に1になるので命題は明らかである。
$a \gt 1$ の場合を証明する。$0 \lt a \lt 1$ の場合も同じように証明できる。
1)${\bf Rat}$上の関数 $f_a(\alpha) = a^{\alpha}$ は単調増加(定理1)なので、
$\{a^{\alpha_{n}}\}_{n}$ は上に有界な単調増加数列、
$\{a^{\beta_{n}}\}_{n}$は下に有界な単調減少数列となる。
このため、「8.2 解析入門(1)」の
「1.2.3 実数列の極限」の定理1から、
これらは、ともに収束することが保証される。
2)$\lim_{n \to \infty}a^{\alpha'_{n}} =\lim_{n \to \infty}a^{\alpha_{n}}(= \underline{a^{\alpha}}) $を示そう。
$\gamma_{n}\triangleq \alpha_{n}-\alpha'_{n}\quad (\in \bf{Rat},n \in \bf{N})$
とおく。
すると、$\lim_{n \to \infty}\gamma_{n}=0 \in \bf{Rat}$
定理1(有理数を累乗とする指数関数の連続性)から、
$\lim_{n \to \infty}a^{\gamma_{n}}=a^0 = 1$
$a^{\gamma_{n}}
=a^{\alpha_{n}-\alpha'_{n}}$
$=\frac{ a^{\alpha_{n}} }{ a^{\alpha'_{n}} } $
故に、
$\lim_{n \to \infty}\frac{ a^{\alpha_{n}} }{ a^{\alpha'_{n}} } = 1$
上式の分子も分母も収束するので
$1= \lim_{n \to \infty}\frac{a^{\alpha_{n}}}{ a^{\alpha'_{n}}}=
\frac{ \lim_{n \to \infty}a^{\alpha_{n}} }{ \lim_{n \to \infty} a^{\alpha'_{n}} }$
3)2)の証明と殆ど同じようにして出来る。
$\{\alpha_n\}_{n=1}^{\infty}$ を $\alpha$ に収束する有理数の単調増加数列
$\{\beta_n\}_{n=1}^{\infty}$ を $\alpha$ に収束する有理数の単調減少数列とする。
$\gamma_{n}\triangleq \beta_{n}-\alpha_{n}\quad (\in \bf{Rat},n \in \bf{N})$
とおく。
すると、$\lim_{n \to \infty}\gamma_{n}=0 \in \bf{Rat}$
定理1(有理数を累乗とする指数関数の連続性)から、
$\lim_{n \to \infty}a^{\gamma_{n}}=a^0 = 1$
$a^{\gamma_{n}}
=a^{\beta_{n}-\alpha_{n}}$
$=\frac{ a^{\beta_{n}} }{ a^{\alpha_{n}} } $
故に、
$\lim_{n \to \infty}\frac{ a^{\beta_{n}} }{ a^{\alpha_{n}} } = 1$
上式の分子も分母も収束するので
$1= \lim_{n \to \infty}\frac{a^{\beta_{n}}}{ a^{\alpha_{n}}}=
\frac{ \lim_{n \to \infty}a^{\beta_{n}} }{ \lim_{n \to \infty} a^{\alpha_{n}} } = \frac{\overline{a^{\alpha}}}{\underline{a^{\alpha}}}$
証明終わり。$\qquad \qquad \qquad \Box$
$\bf{a^{\alpha}の定義 }$
$a$ を任意の正の実数、$\alpha$ を任意の実数とするとき、
$a$ の $\alpha$乗を、
$a^{\alpha} \triangleq \underline{a^{\alpha}} (= \overline{a^{\alpha}})$
で定義する。
$\Large{\bf{定理2}}$
1)任意の正の実数$a$ に対して、その実数乗を上述のように定義すると、
累乗の計算規則を満たす。
2)実数空間 ${\bf R}$ で定義された指数関数
$f_{a}(x)= a^x \quad (x \in {\bf R})$
は、$ a \neq 1$ ならば、一対一関数で
$ a \gt 1$ ならば単調増加、$\quad a \lt 1$ ならば単調減少である
3)$ a \neq 1$ ならば、指数関数$f_{a}(x)= a^x$ は ${\bf R}$から無限開区間$(0,\infty)$の上への、連続関数である。
証明
1)$ a, b $ を任意の正の実数、$\alpha,\quad \beta$を実数とすると、
$a^{\alpha}a^{\beta} = a^{\alpha+\beta} \ (規則1)\quad
(a^{\alpha})^\beta =a^{\alpha \beta} \ (規則2)\quad (ab)^\beta = a^\beta b^\beta \ (規則3)$ を示せばよい。
皆同じように証明できるので、規則1だけを証明する。
実数 $\alpha$ に収束する任意の有理数の単調増加列 $\{\alpha_n\}_{n}$ と、
実数 $\beta$ に収束する任意の有理数の単調増加列 $\{\beta_n\}_{n}$ をとれば、
定理1から、有理数乗では規則1は成り立つので、
$a^{\alpha_n}a^{\beta_n} = a^{\alpha_n+\beta_n} $
極限($\lim_{n\to \infty}$)をとれば、
$\lim_{n\to \infty}(a^{\alpha_n}a^{\beta_n}) = \lim_{n\to \infty}a^{\alpha_n+\beta_n} $
この左辺は極限の性質から$\lim_{n\to \infty}a^{\alpha_n}\lim_{n\to \infty}a^{\beta_n}$ に等しいので、
$\lim_{n\to \infty}a^{\alpha_n}\lim_{n\to \infty}a^{\beta_n}= \lim_{n\to \infty}a^{\alpha_n+\beta_n} \qquad \qquad (a)$
命題6とその直後の$a^{\alpha}$の定義から、
$\lim_{n\to \infty}a^{\alpha_n} = \underline{a^{\alpha}}= a^{\alpha} $
$\lim_{n\to \infty}a^{\beta_n} = \underline{a^{\beta}}= a^{\beta} $
$\lim_{n\to \infty}a^{\alpha_n+\beta_n} = \underline{a^{\alpha+\beta}}= a^{\alpha + \beta} $
この3つの式を式(a)に代入すると、
$a^{\alpha}a^{\beta}=a^{\alpha + \beta} $
累乗規則の1が成り立つことが示せた。
対数と対数関数
1と異なる正の実数 $a$ を考える。
指数関数 $f_{a}(x) = a^x$ は,定理2から、
${\bf R}$ から $(0,\infty)$ の上への、一対一、連続関数である。
定義1
実数 $a$ を $ a\gt 0,\ a\neq 1$ とする。この時、
任意の正の実数 Xに対して、
$a^x = X$
を満たす実数xが唯一つ定まる。
このxを X の$a$ を底とする対数と呼び、$\log_{a}X$ とかく。
指数関数 $f_{a}(x) = a^x$ は
${\bf R}$ から $(0,\infty)$ の上への、一対一関数
なので、逆関数を考えることができる。
定義2
$a$ を1と異なる正の実数とする。
$\log_{a} a^x \triangleq x \qquad \qquad \qquad (1)$
この関数を、$a$ を底とする対数関数とよぶ。
定理1
$a$ を 1と異なる正の実数とする。
1) $a$ を底とする対数関数 $\log_{a}$ は、
指数関数$f_{a}(x)=a^x$の逆関数であり、
$(\log_{a}\cdot f_{a})(x) = x \quad (x \in {\bf R})\qquad \qquad \qquad (2) $
すなわち、
$\log_{a}(a^x) = x \quad (x \in {\bf R})\qquad \qquad \qquad (2') $
と(注参照)、
$(f_{a}\cdot \log_{a})(y) = y \quad \bigl(y \in (0,\infty)\bigr)\qquad \qquad \qquad (3) $
すなわち、
$a^{\log_{a}(y)} = y \quad \bigl(y \in (0,\infty)\bigr)\qquad \qquad \qquad (3') $
を満たす。
2)指数関数$f_{a}(x)=a^x$ は
$(0,\infty)$ から ${\bf R}$ の上への一対一で
連続な関数である。
(注) 2つの関数f、gに対して、その合成関数$(f\cdot g)$ は、
$(f\cdot g)(x)\triangleq f\bigl(g(x)\bigr)$ で定義される。
定理2
$a$ を 1と異なる正の実数とする。
すると
1) 任意の2つの正の実数b、cに対して,
$\qquad \log_{a}b + \log_{a}c = \log_{a}bc \qquad \qquad \qquad (4)$
2) 任意の2つの正の実数 b,c に対して,
$\qquad \log_{a}b - \log_{a}c = \log_{a}\frac{b}{c} \qquad \qquad \qquad (5)$
3) 任意の正の実数 b と任意の実数 c に対して
$\qquad \log_{a}b^c = c \log_{a}b \qquad \qquad \qquad (6)$
証明
1) 指数関数$f_{a}(x)=a^x$ の性質から、
$a^{x_{b}}= b,\quad a^{x_{c}}= c \qquad \qquad \qquad (7)$
を満たす、実数 $x_{b} \quad x_{c}$ がそれぞれ唯一つ定まる。
式(7)から対数関数の定義を用いると、
$\log_{a}b = x_{b} \quad \log_{a}c = x_{c}\qquad \qquad \qquad (8)$
すると、
$\quad \log_{a}b + \log_{a}c = x_b + x_c \quad (式(8)から)$
$=\log_{a} a^{x_b + x_c } \quad (式(1)から)$
$=\log_{a} (a^{x_b} a^{x_c }) \quad (指数関数の性質から)$
$=\log_{a}(bc) \quad (式(7)から) $
2)も同様に証明できる。
3)$X \triangleq \log_{a}b^c$ とおく。すると、対数の定義から、
$a^X = b^c$
$\qquad $ bは正の実数なので、$x_b=\log_{a}b とおくと、 a^{x_b}= b$なので、
$= (a^{x_b})^c = a^{x_b c} \quad (指数関数の性質から)$
故に
$a^X = a^{x_b c}$
指数関数が一対一関数なので、$X = x_b c = c \log_{a}b$
X の定義から、$\log_{a}b^c = c \log_{a}b \qquad \qquad \Box $
定理3 底の変換公式
任意の3つの正の実数 $a(\neq 1),b,c(\neq 1) $ に対して
$\qquad \log_{a}b = \frac{\log_{c}b}{\log_{c}a}\qquad \qquad \qquad (9)$
証明
定理1の式(3')から、
$ \quad a^{\log_{a}b} = b \qquad \qquad \qquad (10)$
底をcとする対数をとれば、
$\log_{c}a^{\log_{a}b} = \log_{c} b$
$\qquad $定理2の式(6)から、$\log_{c}a^{\log_{a}b} = (\log_{a}b)(\log_{c}a)$なので、
$ (\log_{a}b)(\log_{c}a) = \log_{c} b$
$a,\quad c$ は、1と異なる正の実数であるため、$ \log_{c}a \neq 0$ となり、
$\log_{a}b = \frac{\log_{c}b }{\log_{c}a}$
が得られた。
証明終わり。 $\qquad \qquad \qquad \Box $
対数関数
1と異なる正の実数 $a$ を考える。
指数関数 $f_{a}(x) = a^x$ は,定理2から、
${\bf R}$ から $(0,\infty)$ の上への、一対一、連続関数である。
すると、その逆関数$\quad (0,\infty) \ni a^x \to x \in {\bf R} $ が定義できる。
定義
$a$ を1と異なる正の実数とする。
$\log_{a} a^x \triangleq x \qquad \qquad \qquad (1)$
この関数を、$a$ を底とする対数関数とよぶ。
定理1
$a$ を 1と異なる正の実数とする。
1) $a$ を底とする対数関数 $\log_{a}$ は、
指数関数$f_{a}(x)=a^x$の逆関数であり、
$(\log_{a}\cdot f_{a})(x) = x \quad (x \in {\bf R})\qquad \qquad \qquad (2) $
すなわち、
$\log_{a}(a^x) = x \quad (x \in {\bf R})\qquad \qquad \qquad (2') $
と(注参照)、
$(f_{a}\cdot \log_{a})(y) = y \quad \bigl(y \in (0,\infty)\bigr)\qquad \qquad \qquad (3) $
すなわち、
$a^{\log_{a}(y)} = y \quad \bigl(y \in (0,\infty)\bigr)\qquad \qquad \qquad (3') $
を満たす。
2)指数関数$f_{a}(x)=a^x$ は
$(0,\infty)$ から ${\bf R}$ の上への一対一で
連続な関数である。
(注) 2つの関数f、gに対して、その合成関数$(f\cdot g)$ は、
$(f\cdot g)(x)\triangleq f\bigl(g(x)\bigr)$ で定義される。
定理2
$a$ を 1と異なる正の実数とする。
すると
1) 任意の2つの正の実数b、cに対して,
$\qquad \log_{a}b + \log_{a}c = \log_{a}bc \qquad \qquad \qquad (4)$
2) 任意の2つの正の実数 b,c に対して,
$\qquad \log_{a}b - \log_{a}c = \log_{a}\frac{b}{c} \qquad \qquad \qquad (5)$
3) 任意の正の実数 b と任意の実数 c に対して
$\qquad \log_{a}b^c = c \log_{a}b \qquad \qquad \qquad (6)$
証明
1) 指数関数$f_{a}(x)=a^x$ の性質から、
$a^{x_{b}}= b,\quad a^{x_{c}}= c \qquad \qquad \qquad (7)$
を満たす、実数 $x_{b} \quad x_{c}$ がそれぞれ唯一つ定まる。
式(7)から対数関数の定義を用いると、
$\log_{a}b = x_{b} \quad \log_{a}c = x_{c}\qquad \qquad \qquad (8)$
すると、
$\quad \log_{a}b + \log_{a}c = x_b + x_c \quad (式(8)から)$
$=\log_{a} a^{x_b + x_c } \quad (式(1)から)$
$=\log_{a} (a^{x_b} a^{x_c }) \quad (指数関数の性質から)$
$=\log_{a}(bc) \quad (式(7)から) $
2)も同様に証明できる。
3)$X \triangleq \log_{a}b^c$ とおく。すると、対数の定義から、
$a^X = b^c$
$\qquad $ bは正の実数なので、$x_b=\log_{a}b とおくと、 a^{x_b}= b$なので、
$= (a^{x_b})^c = a^{x_b c} \quad (指数関数の性質から)$
故に
$a^X = a^{x_b c}$
指数関数が一対一関数なので、$X = x_b c = c \log_{a}b$
X の定義から、$\log_{a}b^c = c \log_{a}b \qquad \qquad \Box $
定理3 底の変換公式
任意の3つの正の実数 $a(\neq 1),b,c(\neq 1) $ に対して
$\qquad \log_{a}b = \frac{\log_{c}b}{\log_{c}a}\qquad \qquad \qquad (9)$
証明
定理1の式(3')から、
$ \quad a^{\log_{a}b} = b \qquad \qquad \qquad (10)$
底をcとする対数をとれば、
$\log_{c}a^{\log_{a}b} = \log_{c} b$
$\qquad $定理2の式(6)から、$\log_{c}a^{\log_{a}b} = (\log_{a}b)(\log_{c}a)$なので、
$ (\log_{a}b)(\log_{c}a) = \log_{c} b$
$a,\quad c$ は、1と異なる正の実数であるため、$ \log_{c}a \neq 0$ となり、
$\log_{a}b = \frac{\log_{c}b }{\log_{c}a}$
が得られた。
証明終わり。 $\qquad \qquad \qquad \Box $