物理/8章の付録
提供: Internet Web School
目次 |
8章の付録
問の解答
問
$\lim_{n\to \infty}(1+\frac{1}{n})^n$ が存在し、2より大きく3以下であることを証明する。
(1)準備; 2項定理;を用いた展開
$a_n\triangleq (1+\frac{1}{n})^{n} \qquad (n は自然数)$ とおく。
すると、
$2 \leq a_1=1+\frac{1}{1}=2\quad \lt a_2=(1+\frac{1}{2})^{2} =2\frac{1}{4}$である。
以下に、数列 $\{a_n\}_{n=1}^{\infty}$ が単調増大で、有界(2より大、3より小)である事を示す。
するとテキストの定理により、この数列は2より大きく、3以下のある実数に収束することが分かる。
nが3以上の自然数の時は、$a_n$を2項定理を用いて展開すると
$a_n=(1+\frac{1}{n})^{n}=\sum_{m=0}^{n}{}_n\mathrm{C}_{m}1^{n-m}(\frac{1}{n})^m \qquad \qquad (1)$
ここで ${}_n\mathrm{C}_{m}$ は、n個のものからm個取り出す取り出し方の総数で、
mが1以上でn 以下の自然数の時は
${}_n\mathrm{C}_{m}=\frac{n!}{m!(n-m)!} \qquad \qquad (2)$
ここで、m が1以上の自然数の時は $ m!\triangleq 1\cdot 2\cdot 3 \cdots (m-1)\cdot m$
mが零の時は $\quad 0!\triangleq 1 $ と定義。
すると、
${}_n\mathrm{C}_{0}=\frac{n!}{0!n!}=1\qquad \qquad (3)$
$m \geq 1$のとき、${}_n\mathrm{C}_{m} =\frac{n!}{m!(n-m)!}=\frac{n\cdot (n-1)\cdot (n-2) \cdots \Bigl(n-(m-1)\Bigr) }{m!} \qquad (4)$
式(1)に式(2)を代入し,式(3)、(4)を利用して計算すると
$a_n = 1+\sum_{m=1}^{n}\frac{n(n-1)(n-2)\cdots \Bigl(n-(m-1)\Bigr)}{m!}1^{n-m}(\frac{1}{n})^m $
$=2+\sum_{m=2}^{n}\frac{1(1-\frac{1}{n})(1-\frac{2}{n})\cdots (1-\frac{m-1}{n})}{m!}\qquad \qquad (5)$
ここで、n より小さい全ての自然数 i に対して
$0 \lt 1-\frac{i}{n} \lt 1 $ なので、
$ 2 \lt a_n \lt 2+\sum_{m=2}^{n}\frac{1}{m!} \qquad \qquad \qquad (6)$
(2)すべての2以上の自然数 n に関して、
$ 2 \lt a_n \lt 3 \qquad \qquad \qquad (7)$
であることを示す。
式(6)から
$2\lt a_n$,
$a_n \lt 2+\sum_{m=2}^{n}\frac{1}{m!} \qquad \qquad (8)$
右辺の m は2以上の自然数なので、
$\frac{1}{m!} \leq \frac{1}{(m-1)m}=\frac{1}{m-1}-\frac{1}{m}$
である。故に、
$a_n \lt 2+\sum_{m=2}^{n}(\frac{1}{m-1}-\frac{1}{m})=2+(1-\frac{1}{n})=3-\frac{1}{n}\lt 3$
(3)数列 $\{a_n\}_{n=1}^{\infty}$ は単調増加
$n \geq 2$ の時、常に $a_n \lt a_{n+1}$ を示せばよい。
式(5)を利用すると(注参照)、
$a_{n+1}=2+\sum_{m=2}^{n+1}\frac{1(1-\frac{1}{n+1})(1-\frac{2}{n+1})\cdots (1-\frac{m-1}{n+1})}{m!}$
すると、
$a_{n+1} - a_n = \sum_{m=2}^{n+1}\frac{1(1-\frac{1}{n+1})(1-\frac{2}{n+1})\cdots (1-\frac{m-1}{n+1})}{m!} - \sum_{m=2}^{n}\frac{1(1-\frac{1}{n})(1-\frac{2}{n})\cdots (1-\frac{m-1}{n})}{m!} $
$\quad$ 右辺の第一項の和を2つに分けると、
$= \frac{1(1-\frac{1}{n+1})(1-\frac{2}{n+1})\cdots (1-\frac{n}{n+1})}{m!}$
$\quad + \sum_{m=2}^{n}\frac{1(1-\frac{1}{n+1})(1-\frac{2}{n+1})\cdots (1-\frac{m-1}{n+1})}{m!} - \sum_{m=2}^{n}\frac{1(1-\frac{1}{n})(1-\frac{2}{n})\cdots (1-\frac{m-1}{n})}{m!}$
$ = \frac{
1(1-\frac{1}{n+1})(1-\frac{2}{n+1})\cdots (1-\frac{n}{n+1})
}{m!}$
$\quad + \sum_{m=2}^{n}\frac{
1(1-\frac{1}{n+1})(1-\frac{2}{n+1})\cdots (1-\frac{m-1}{n+1})
-1(1-\frac{1}{n})(1-\frac{2}{n})\cdots (1-\frac{m-1}{n})}{m!}$
上の式で、全ての$i\in \{1,2,,,,n\}$に対して,$(1-\frac{i}{n+1})\gt 0$と$(1-\frac{i}{n+1})\gt (1-\frac{i}{n})$ なので、
$a_{n+1} - a_n \gt 0$
(注)式(3)のnに n+1 を代入すればよい。
ネイピア数 e について
定義;$e\triangleq \lim_{}(1+\frac{1}{n})^n$ をネイピア数と呼ぶ。
命題1
(1)$ 2 \lt e \leq 3$
(2)$e=\sum_{m=0}^{\infty}\frac{1}{m!} \qquad ただし、0!\triangleq 1,\quad m!\triangleq 1\cdot 2\cdot 3\cdots (m-1)\cdot m \qquad \qquad (9)$
三角関数の微分
準備
次の命題が、三角関数の微分を求めるうえで中心的役割を果たす。
命題2
$\lim_{\theta\to 0,\theta\neq 0}\frac{\sin \theta}{\theta}=1$
証明
まず、$\theta$ を正に保ちながら零に近づける場合を考える。
すると、$ 0 \lt \theta \lt \pi/2 $ と考えて良い。
点Oを中心にし、半径1の円を考え、円周上に一点Aをさだめる。
図のように、円周上の点Bを、線分OBが直線OAとなす角がx(ラジアン)となるようにとる。
図から$\triangle{OAB} \subset 扇形OAB \subset \triangle{OAP} $
$\quad$ ここで、点PはAを通り線分OAと垂直な直線と半直線OBの交点。
すると、
$\triangle{OAB}の面積 \lt 扇形OAB の面積 \lt \triangle{OAP}の面積$
ここで、$\triangle{OAB}の面積=\frac{1\cdot \sin{\theta}}{2},\quad 扇形OAB の面積=\pi\cdot 1^{2}\cdot \frac{\theta}{2\pi}\quad \triangle{OAP}の面積=\frac{1\cdot \tan{\theta}}{2}$なので、
$\frac{\sin{\theta}}{2} \lt \frac{\theta}{2}\lt \frac{\tan{\theta}}{2}=\frac{\sin{\theta}}{2\cos{\theta}}\qquad $各項を2倍すると、
$\sin{\theta}\lt \theta \lt \frac{\sin{\theta}}{\cos{\theta}}$
$\quad$ここで $\sin{\theta}\gt 0$ なので、これで上式の各項を割ると、
$1 \lt \frac{\theta}{\sin{\theta}} \lt \frac{1}{\cos{\theta}}$
$1 \gt \frac{\sin{\theta}}{\theta} \gt \cos{\theta}$
故に、極限の性質から
$1 \geq \lim_{\theta\to 0,\theta\neq 0}\frac{\sin \theta}{\theta} \geq \lim_{\theta\to 0,\theta\neq 0}\cos{\theta}=1$
これより、$\lim_{\theta\to 0,\theta\neq 0}\frac{\sin \theta}{\theta}=1$ が得られる。
定理1 三角関数の微分
(1)$\frac{d}{d\theta}\sin{\theta}=\cos{\theta}$
(2)$\frac{d}{d\theta}\cos{\theta}=-\sin{\theta}$
証明
(1); $\frac{d}{d\theta}\sin{\theta} \triangleq \lim_{h\to 0,h\neq 0}\frac{\sin (\theta+h)-\sin \theta}{h}$
ここで、
$\sin (\theta+h)-\sin \theta = \sin \bigl((\theta + \frac{h}{2})+\frac{h}{2}\bigr) - \sin \bigl((\theta + \frac{h}{2})-\frac{h}{2}\bigr)$
サイン関数の加法定理を適用すると
$=\sin (\theta + \frac{h}{2})\cos \frac{h}{2} + \cos (\theta + \frac{h}{2})\sin \frac{h}{2} - \Bigl( \sin (\theta + \frac{h}{2})\cos \frac{h}{2} - \cos (\theta + \frac{h}{2})\sin \frac{h}{2} \Bigr) = 2\cdot \cos (\theta + \frac{h}{2})\sin \frac{h}{2}$
故に、
$\frac{d}{d\theta}\sin{\theta} \triangleq \lim_{h\to 0,h\neq 0}\frac{\sin (\theta+h)-\sin \theta}{h} = \lim_{h\to 0,h\neq 0}\frac{2\cdot \cos (\theta + \frac{h}{2})\sin \frac{h}{2}}{h}=\lim_{h\to 0,h\neq 0}\cos (\theta + \frac{h}{2})\frac{\sin \frac{h}{2}}{h/2}$
$=\lim_{h\to 0,h\neq 0}\cos (\theta + \frac{h}{2})\lim_{h\to 0,h\neq 0}\frac{\sin \frac{h}{2}}{h/2}$
$\quad $ ここで、
$\quad \lim_{h\to 0,h\neq 0}\cos (\theta + \frac{h}{2}) = \cos \theta$
$\quad \lim_{h\to 0,h\neq 0}\frac{\sin \frac{h}{2}}{h/2} = 1 \quad (上の命題2より)$
$\quad $なので、
$=\cos \theta$
指数関数と対数関数
実数の累乗
$a$ を任意の実数、$n$ を2以上の自然数とする。
$a^1=a,\quad a^2=a\cdot a,\quad a^3=a^2\cdot a=a\cdot a\cdot a ,\quad \cdots \quad a^n=a^{n-1}\cdot a, \cdots$
を総称して、a の累乗と呼ぶ。
$a^n$ を$a $ の n 乗 、$n$ をその指数と呼ぶ。
この累乗が次のような計算規則を満たすことは、容易に証明できる。
命題1
$ a,b $ を任意の実数、$ m, n $ を任意の自然数とすると、
(1) $a^{m}a^{n} = a^{m+n} $
(2) $(a^{m})^n =a^{m n} $
(3) $(ab)^n = a^n b^n $
そこで次の累乗に関する計算規則を定義する。
累乗に関する計算規則
$ a, b $ を任意の正の実数、$\alpha,\quad \beta$を指数を表わす数とすると、
(1) $a^{\alpha}a^{\beta} = a^{\alpha+\beta} \qquad \qquad \qquad (累乗規則1)$
(2) $(a^{\alpha})^\beta =a^{\alpha \beta} \qquad \qquad \qquad (累乗規則2)$
(3) $(ab)^\beta = a^\beta b^\beta \qquad \qquad \qquad (累乗規則3)$
この計算規則(3)から、$1^\beta \equiv 1$ であることが分かる。
何故ならば $b=1$の時、$(a・1)^\beta = a^\beta 1^\beta $ となり、 $a^\beta \neq 0$ であるから。
そこで今後は $a \neq 1$ の場合だけを考える。
命題2
(1)$ a $ を1より小さい正の実数とすると、数列 $\{a^{n}\}_{n=1}^{\infty}$ は単調減少し、零に収束。
(2)$ a $ を1より大きい正の実数とすると、数列 $\{a^{n}\}_{n=1}^{\infty}$ は単調増加し、いくらでも大きくなる(無限大に発散)。
これより、累乗に関する3つの規則が、そのまま成り立つようにしながら、指数を実数まで拡げよう。
指数の整数への拡張
まず指数を、累乗に関する3つの規則が成り立つようにしながら、整数に拡張する。
累乗の定義から、
$a \neq 0,1$ の時は、任意の自然数m、nに対し、
$a^m \div a^n = a^{m-n} \qquad (m\gt n) \qquad \qquad (1)$
$\qquad \qquad = 1 \qquad (m = n)\qquad \qquad \qquad(2)$
$\qquad \qquad = \frac{1}{a^{n-m}} \qquad (m \lt n)\qquad \qquad (3)$
であることが分かる。
これを一つの式 $a^{m-n}$ で表わせるように、a の指数を取決めたい。
そのためには、指数が零の時、$a^0 \triangleq 1$、
指数 $m-n$ が負数の時 $a^{m-n} \triangleq \frac{1}{a^{n-m}}$
と定義すればよい。
言い換えると、$a (\neq 0,1) $ の指数nが 零と負の整数のとき、
$a^0 \triangleq 1, \qquad a^n \triangleq \frac{1}{a^{-n}} \qquad (n\lt 0)\qquad \qquad (4)$
と定義する。
すると、指数が整数の時、3つの累乗規則を満たすことは、容易に確かめられる。
指数の有理数への拡張
これ以降、有理数全体のなす集合を${\bf Rat}$とかく。
$ a (\neq 1)$ を任意の正の実数、 $\frac{m}{n}$ を任意の有理数のとき、
$ a $ の有理数乗 $a^{\frac{m}{n}}$ を、計算規則を満たすように定義しよう。
指数n を任意の自然数(正の整数)、 m を任意の整数と仮定してよい。
$\qquad $(注)nが負の時は$a^{\frac{m}{n}} = a^{\frac{-m}{-n}}$ なので、
$\qquad \quad -n,-m $を改めて$n,m$ と置けば良い。$\Box$
累乗規則(2)を満たすように定義するには、
$(a^{\frac{m}{n}})^{n} = (a^{\frac{m}{n}})^{\frac{n}{1}} = a^{m}$
でなければならない。
これは、$a^{\frac{m}{n}}$ が $a^{m}$ のn乗根であることを示す。
しかしnが偶数のときは、$-a^{\frac{m}{n}}$ も$a^{m}$ のn乗根となるので、
正のn乗根 のほうを、$a^{\frac{m}{n}}$ とかく。
定義 正の実数の有理数乗
$a$を正の実数とする。
$a^{\frac{m}{n}}$ とは、
$a^{m}$ の正のn乗根である。
すなわち、
$(a^{\frac{m}{n}})^{n} =a^{m} $を満たす正の実数である。
最初に、この定義できちんと正の実数が一つだけ決まることを証明しよう。
$a=1$のときは、n乗すると1になる正数は1だけなので
$1^{\frac{m}{n}}=1 $
であることが分かるので、$a \neq 1$ の場合を考える。
命題3
$a \neq 0,1$ を任意の正の実数、$ m$ を任意の整数,$n$を任意の自然数とする。
すると、n 乗すると $a^{m}$ になる正の実数 $ b $ (i.e. $\quad b^n = a^{m}$)が存在し、ただ一つに限る。
証明
(1) 存在性
$ f(x) \triangleq x^n $ という、零と正の実数の上で定義された、関数を考える。
この関数はxが増加するにつれて、連続的に、零から正の無限大に狭義に単調に増加(注参照)していく。
そこで、$B\triangleq \{x \in [0,\infty)\ |\ x^n \leq a^{m} \}$ という集合を考える。
この集合は、上に有界な区間になり、実数の連続性から上限(sup)$b$を持つ。
この時、$ b \in B, \quad b^n = a^{m}$ であることを示そう。
$b$ が集合$B (\in {\bf R})$の上限なので、任意の自然数nに対して、
$0 \leq b - b_{n} \lt \frac{1}{n} $
を満たす $ b_{n} \in B $ が存在する。
明らかに
$ \lim_{n \to \infty}b_{n} = b $
すると、関数 $ f(x) \triangleq x^n $ は連続なので、
$ \lim_{n \to \infty}b_{n}^n = b^n \qquad \qquad \qquad (a)$
ところが$ b_{n} \in B \triangleq \{x \in [0,\infty)|x^n \leq a^{m} \}$なので、
$ b_{n}^n \leq a^{m} \qquad \qquad \qquad (b)$
式(a)、(b) から、$ b^n \leq a^{m}$ がえられるので、
$ b \in B$
が示せた。(従って、Bは閉区間 [o,b] である。)
$b^n = a^{m}$ であることを背理法を使って示そう。
もし、$b^n \lt a^{m}$ だとすると、関数 $ f(x) = x^n $ は連続なので
充分小さな正の実数$\delta$ をとると、$(b + \delta) ^n \lt a^{m}$ を満たす。
すると $(b + \delta) \in B$ となり、
$b$が B の上限であることに矛盾してしまう。
故に、背理法により、$b^n = a^{m} $ が証明できた。
(2)一意性
関数 $ f(x) = x^n $ は狭義の単調増加関数なのでb以外の数b'($\neq b$)では、
${b'}^n \neq b^n =a^m$
(証明終り) $ \qquad \qquad \Box$
(注) 関数fが狭義単調増加とは、$ x \lt y \Rightarrow f(x) \lt f(y) $ を満たすこと。
命題4
任意の正の実数 $a \neq 1$ にたいして、その有理数乗を上記のように定義すると
3つの累乗規則 (1)~(3) が成り立つ。
証明;
1) 累乗規則(1)が成り立つことを示す。
2個の有理数の指数を 自然数$n,\quad \tilde{n}$と整数$m,\quad \tilde{m}$ を用いて、
$\alpha = \frac{m}{n},\quad \beta = \frac{\tilde{m}}{\tilde{n}}$と表現する。
すると、累乗規則(1)は、次のように表される。
$a^{\frac{m}{n}}a^{\frac{\tilde{m}}{\tilde{n}}} = a^{\frac{m}{n}+\frac{\tilde{m}}{\tilde{n}}} $
この左辺を $b \triangleq a^{\frac{m}{n}}a^{\frac{\tilde{m}}{\tilde{n}}}$,
右辺を $c \triangleq a^{\frac{m}{n}+\frac{\tilde{m}}{\tilde{n}}}$ とおく。
$b^{n \tilde{n}} = c^{n \tilde{n}} \qquad \qquad \qquad (a)$
であることを示せば、$b = c$ が得られ,
累乗規則(1)が成立することが分かる。
まず左辺を考える。
$b^{n \tilde{n}} = (a^{\frac{m}{n}}a^{\frac{\tilde{m}}{\tilde{n}}})^{n \tilde{n}}$
指数が自然数の累乗規則(3)から
$ = (a^{\frac{m}{n}})^{n \tilde{n}}(a^{\frac{\tilde{m}}{\tilde{n}}})^{n \tilde{n}}$
指数が自然数の累乗規則(2)から
$= \Bigl((a^{\frac{m}{n}})^{n}\Bigr)^{\tilde{n}}\Bigl((a^{\frac{\tilde{m}}{\tilde{n}}})^{\tilde{n}}\Bigr)^{n}$
実数の有理数乗の定義から、
$ = (a^{m})^{\tilde{n}}(a^{\tilde{m}})^{n}$
指数が整数の累乗規則(2)から
$ = a^{m \tilde{n}}a^{\tilde{m}n}$
指数が整数の累乗規則(1)から
$ = a^{m \tilde{n} + \tilde{m}n}$
故に、$b^{n \tilde{n}} = a^{m \tilde{n} + \tilde{m}n}$
次に、右辺を考える。
$c^{n \tilde{n}} = (a^{\frac{m}{n}+\frac{\tilde{m}}{\tilde{n}}})^{n \tilde{n}}$
$ = (a^{ \frac{m\tilde{n}+n\tilde{m}}{n\tilde{n}}})^{n \tilde{n}}$
実数の有理数乗の定義から、
$ = a^{m\tilde{n} + n\tilde{m}} = b^{n \tilde{n}}$
これで、式(a)が示され、累乗規則(1)が成り立つことが証明できた。
2)累乗規則(2)と累乗規則(3)が成り立つことは読者がしてください。
証明終わり。
指数が有理数の場合,命題2は次のように拡張出来る。
命題5
${\bf Rat}$の上で定義される関数
$f_a(\alpha) \triangleq a^{\alpha} \qquad (\alpha \in {\bf Rat})$を考える。
1)$a$ を1より大きい正の実数とすると、
$f_a$は単調増大で
$\lim_{\alpha \to \infty,\alpha \in {\bf Rat}}a^{\alpha} = \infty \quad \lim_{\alpha \to -\infty}f_a(\alpha) = 0 $
2)$a$ が1より小さい正の実数のとき、
$f_a$は単調減少し、
$\lim_{\alpha \to \infty,\alpha \in {\bf Rat}}f_a(\alpha) = 0\quad \lim_{\alpha \to -\infty,\alpha \in {\bf Rat}}f_a(\alpha) = \infty $
3)$a = 1$ のとき、$f_a \equiv 1$
証明
1)のみ証明する。2)の場合も同様に証明できる。
① $\frac{m}{n} \lt \frac{m'}{n'} ,\quad n,m \in {\bf N} $ とすると、
$a^{\frac{m}{n}} \lt a^{\frac{m'}{n'}}$ を示そう。
$\alpha \triangleq a^{\frac{m'}{n'}} \div a^{\frac{m}{n}} \gt 1$
を示せばよい。
正数の有理数乗の計算規則から、
$\alpha \triangleq a^{\frac{m'}{n'}} \div a^{\frac{m}{n}}=a^{\frac{m'}{n'}-\frac{m}{n}}$
$=a^{ \frac{m'n-n'm}{n'n} }$
故に、
${\alpha}^{n'n} = a^{m'n-n'm}$
$\qquad \frac{m}{n} \lt \frac{m'}{n'}$ から、
$\qquad m'n-n'm \gt 0 $なので、$a^{m'n-n'm} \gt 1$であり
$ \gt 1$
故に、 ${\alpha}^{n'n} \gt 1$
自然数乗すると1より大きくなる正の実数は1より大きい実数しかないので、
$\alpha \gt 1$ が得られた。
② $\lim_{\alpha \to \infty,\alpha \in {\bf Rat}}a^{\alpha}= \infty $を示そう。
関数 $f_a(\alpha)$ は単調増加(①で証明)なので、
$\lim_{n \to \infty,n \in {\bf N}}a^n = \infty $
を示せばよいが、これは自明である。
③ $\lim_{\alpha \to -\infty,\alpha \in {\bf Rat}}f_a(\alpha) = 0 $
も、同様にして示せる。
証明終わり $\qquad \qquad \qquad \Box$
以上の結果をまとめて、次の定理を得る。
$\Large {\bf{定理1}}$
$a \neq 0,1$ の正の実数とする。
(1)$ a $ の有理数乗 $a^{\frac{m}{n}}\quad(m;整数、n \in {\bf N})$ を$a^{m}$の正の$n$乗根で定義すると、
累乗に関する計算規則
$ a, b $ を任意の正の実数、$\alpha,\beta \in {\bf Rat} $を指数とすると、
$\quad$ 1) $a^{\alpha}a^{\beta} = a^{\alpha+\beta} \qquad \qquad (累乗規則1)$
$\quad$ 2) $(a^{\alpha})^\beta =a^{\alpha \beta} \qquad \qquad (累乗規則2)$
$\quad$ 3) $(ab)^\beta = a^\beta b^\beta \qquad \qquad (累乗規則3)$
を満たす。
(2)${\bf Rat}$の上で定義される関数
$f_a(\alpha) \triangleq a^{\alpha} \qquad (\alpha \in {\bf Rat})$を考えると、
$\quad$1)$a\gt 1$ のとき、 $f_a$は狭義の単調増大(従って一対一)で、
$\quad$ $\lim_{\alpha \to \infty,\alpha \in {\bf Rat}}a^{\alpha} = \infty \quad \lim_{\alpha \to -\infty}f_a(\alpha) = 0 $
$\quad$ 2)$a \lt 1$ のとき、 $f_a$は狭義の単調減少(従って一対一)で、
$\lim_{\alpha \to \infty,\alpha \in {\bf Rat}}f_a(\alpha) = 0\quad \lim_{\alpha \to -\infty,\alpha \in {\bf Rat}}f_a(\alpha) = \infty $
$\quad$ 3)$a = 1$ のとき、$f_a \equiv 1$
(3)関数 $f_a(\alpha) \triangleq a^{\alpha} \quad (\alpha \in {\bf Rat})$は連続関数である。
すなわち、
$\frac{m_k}{n_k}\to \frac{m}{n} \quad ({\bf N} \ni k\to \infty) \quad (m_k,m は整数、 n_k,n は自然数)$
ならば、
$ a^{\frac{m_k}{n_k}} \to a^{\frac{m}{n}}$
証明
命題(1)、(2)はすでに証明したことなので、(3)だけを証明する。
$|a^{ \frac{m_k}{n_k} } - a^{ \frac{m}{n} }| =
|a^{ \frac{m}{n} }| |a^{ \frac{m_k}{n_k}- \frac{m}{n} }-1|$ なので、
$\lim_{\frac{m_k}{n_k}\to \frac{m}{n} }|a^{\frac{m_k}{n_k}- \frac{m}{n}}-1| = 0$
を、示せばよい。
$\frac{\tilde{m_k}}{\tilde{n_k}}\triangleq \frac{m_k}{n_k}- \frac{m}{n}$ とおくと、
$\lim_{ \frac{ \tilde{m_k} }{ \tilde{n_k} }\to 0 }
|a^{\frac{ \tilde{m_k} }{ \tilde{n_k} } } - 1|= 0$
を示せばよい。
このために、次の補題をまず証明する。
補題
$\lim_{n\to \infty}|a^{ \frac{1}{n} }- 1|=0 \qquad \quad (b) $
$\lim_{n\to \infty}|a^{ \frac{-1}{n} }- 1|=0 \qquad \quad (c)$
補題の証明
1) 式(b)を背理法で証明する。
もし式(b)が成立しないとする。
すると或る小さな正数$\epsilon$ が存在し、
どのような自然数 $n_0$ をとっても、ある自然数$n \gt n_0$ が存在して
$|a^{ \frac{1}{n} }- 1| \geq \epsilon$
となる。(注参照)
すると、自然数の部分列 $\{ n_k \}_{k\in {\bf N}}
\quad (n_k \lt n_{k+1},k=1,2,3,\cdots)$ が存在して、
$(\forall k\in {\bf N})( |a^{ \frac{1}{n_k} }- 1| \geq \epsilon)\qquad (d)$
となる。
① $a \gt 1$ の場合
$a^{ \frac{1}{n_k} } \gt 1$なので、
$(\forall k\in {\bf N})( a^{ \frac{1}{n_k} }- 1 \geq \epsilon)$
すなわち、
$(\forall k\in {\bf N})( a^{ \frac{1}{n_k} } \geq 1+\epsilon)$
両辺を$n_k$乗して
$(\forall k\in {\bf N})(a \geq (1+\epsilon)^{n_k})$
2項定理から
$(1+\epsilon)^{n_k} \geq 1+n_k\epsilon$
であることがわかるので、
$(\forall k\in {\bf N})(a \geq 1+n_k\epsilon ) \qquad \qquad (e)$
$n_k \to \infty \quad (k \to \infty)$ なので、
式(e)から、$a = \infty $ となり、矛盾が生じてしまう。
② $a \lt 1$ の場合も同様にして、矛盾が生じることが示せる。
③ 故に、式(b)が成立しないと仮定すると矛盾が生じるので、
背理法により、式(b)が成立することが、証明できた。
2)式(c)の証明も同様にしてできるので省略する。$\Box$
任意の正数$\epsilon$ に対して、ある番号$k_{\epsilon}$が定まって、
$k \geq k_{\epsilon}$というすべての自然数$k$に対して、
$|a^{\frac{ \tilde{m_k} }{ \tilde{n_k} } } - 1|\lt \epsilon$
を示せば、
$\lim_{ \frac{ \tilde{m_k} }{ \tilde{n_k} }\to 0 }
|a^{\frac{ \tilde{m_k} }{ \tilde{n_k} } } - 1|= 0$
が示せて、証明が終了する。
補題により、$\epsilon$ に対して、ある番号$n_0$をさだめ,
$n \geq n_0$ならば、
$|a^{ \frac{1}{n} }- 1|\lt \epsilon$
$|a^{ \frac{-1}{n} }- 1|\lt \epsilon$
が成立するようにできる。
$\lim_{k \to \infty}\frac{ \tilde{m_k} }{ \tilde{n_k} }= 0 $
なので、
自然数$n_0$に対して、
ある番号$k(n)\in {\bf N}$ が存在して、
$k(n)$以上のどんな自然数$k$に対しても、
$\frac{-1}{n_0}\lt \frac{ \tilde{m_k} }{ \tilde{n_k}}\lt \frac{1}{n_0}$
すると指数関数$f_{a}(\alpha)=a^{\alpha}$ の単調性から、
$a^{ \frac{ \tilde{m_k} }{ \tilde{n_k} } }$ は、$a^{\frac{-1}{n_0}}$と$a^{\frac{-1}{n_0} }$の間の数となり、
$|a^{\frac{ \tilde{m_k} }{ \tilde{n_k} } } - 1|\lt \epsilon$
が示せた。
定理の証明終わり。 $\qquad \qquad \qquad \qquad \Box$
指数の実数への拡張
任意の実数 $\alpha$ に対して 指数 $a^{\alpha}$ を次のように定義する。
$\bf{定義}$
1)$\{\alpha_n\}_{n=1}^{\infty}$ を $\alpha$ に収束する有理数の単調増加数列とするとき、
$\underline{a^{\alpha}} \triangleq \lim_{n \to \infty}a^{\alpha_{n}}\qquad (a)$
2)$\{\beta_n\}_{n=1}^{\infty}$ を $\alpha$ に収束する有理数の単調減少数列とするとき、
$\overline{a^{\alpha}} \triangleq \lim_{n \to \infty}a^{\beta_{n}}\qquad (b)$
$\bf{命題}$
1)定義の式(a)、(b) は収束する。
2)$\alpha$ に収束する、
別の有理数の単調増加数列$\{\alpha'_n\}_{n=1}^{\infty}$と単調減少数列$\{\beta'_n\}_{n=1}^{\infty}$ をとっても、
極限値は変わらない。すなわち、
$\lim_{n \to \infty}a^{\alpha'_{n}} = \underline{a^{\alpha}} $
$\lim_{n \to \infty}a^{\beta'_{n}} = \overline{a^{\alpha}} $
証明
$a \gt 1$ の場合を証明する。$0 \lt a \lt 1$ の場合も同じように証明できる。
1)${\bf Rat}$上の関数 $f_a(\alpha) = a^{\alpha}$ は単調増加(定理1)なので、
$\{a^{\alpha_{n}}\}_{n}$ は上に有界な単調増加数列、
$\{a^{\beta_{n}}\}_{n}$は下に有界な単調減少数列となる。
このため、「8.2 解析入門(1)」の
「1.2.3 実数列の極限」の定理1から、
これらは、ともに収束することが保証される。
2)$\lim_{n \to \infty}a^{\alpha'_{n}} = \underline{a^{\alpha}} =\lim_{n \to \infty}a^{\alpha_{n}}$を示そう。
$\gamma_{n}\triangleq \alpha_{n}-\alpha'_{n}\quad (\in \bf{Rat},n \in \bf{N})$
とおく。
すると、$\lim_{n \to \infty}\gamma_{n}=0 \in \bf{Rat}$
定理1(有理数を累乗とする指数関数の連続性)から、
$\lim_{n \to \infty}a^{\gamma_{n}}=a^0 = 1$
$a^{\gamma_{n}}
=a^{\alpha_{n}-\alpha'_{n}}$
$=\frac{ a^{\alpha_{n}} }{ a^{\alpha'_{n}} } $
故に、
$\lim_{n \to \infty}\frac{ a^{\alpha_{n}} }{ a^{\alpha'_{n}} } = 1$
上式の分子も分母も収束するので
$1= \lim_{n \to \infty}\frac{a^{\alpha_{n}}}{ a^{\alpha'_{n}}}=
\frac{ \lim_{n \to \infty}a^{\alpha_{n}} }{ \lim_{n \to \infty} a^{\alpha'_{n}} }$
証明終わり。$\qquad \qquad \qquad \Box$
$\bf{命題}$
$\underline{a^{\alpha}} = \overline{a^{\alpha}} $
証明
証明終わり
定理2
指数を実数に拡張しても、累乗の計算規則を満たす。
定理3
$ a \neq 0,1$ である正の実数$ a $を考える。
実数空間 ${\bf R}$ で定義された指数関数
$f_{a}(x)= a^x \quad (x \in {\bf R})$
は、次の性質をもつ。
(1)$(0,\infty)$ の上への、一対一関数
(2)$ a \gt 1$ ならば単調増加、$\quad a \lt 1$ ならば単調減少
(3)連続関数
対数と対数関数
1と異なる正の実数 $a$ を考える。
指数関数 $f_{a}(x) = a^x$ は,命題2から、
${\bf R}$ から $(0,\infty)$ の上への、一対一、連続関数である。
定義1
実数 $a$ を $ a\gt 0,\ a\neq 1$ とする。この時、
任意の正の実数 Xに対して、
$a^x = X$
を満たす実数xが唯一つ定まる。
このxを X の$a$ を底とする対数と呼び、$\log_{a}X$ とかく。
指数関数 $f_{a}(x) = a^x$ は
${\bf R}$ から $(0,\infty)$ の上への、一対一関数
なので、逆関数を考えることができる。
定義2
$a$ を1と異なる正の実数とする。
$\log_{a} a^x \triangleq x \qquad \qquad \qquad (1)$
この関数を、$a$ を底とする対数関数とよぶ。
定理1
$a$ を 1と異なる正の実数とする。
1) $a$ を底とする対数関数 $\log_{a}$ は、
指数関数$f_{a}(x)=a^x$の逆関数であり、
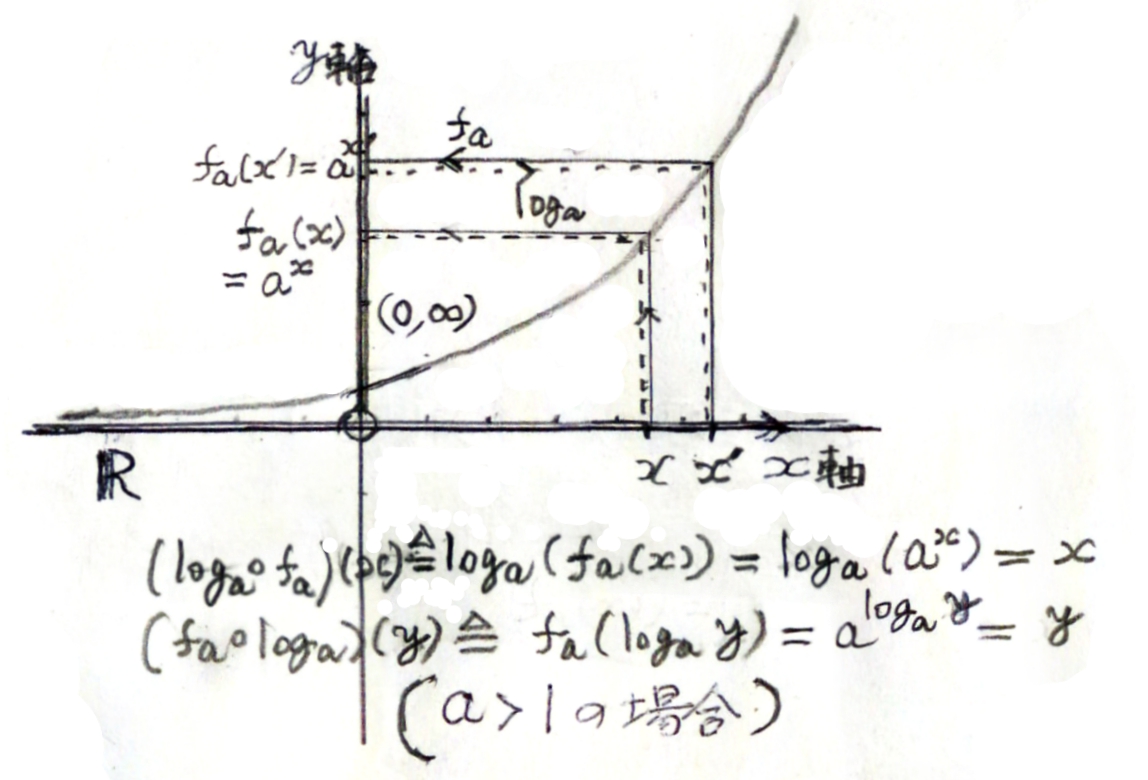
$(\log_{a}\cdot f_{a})(x) = x \quad (x \in {\bf R})\qquad \qquad \qquad (2) $
すなわち、
$\log_{a}(a^x) = x \quad (x \in {\bf R})\qquad \qquad \qquad (2') $
と(注参照)、
$(f_{a}\cdot \log_{a})(y) = y \quad \bigl(y \in (0,\infty)\bigr)\qquad \qquad \qquad (3) $
すなわち、
$a^{\log_{a}(y)} = y \quad \bigl(y \in (0,\infty)\bigr)\qquad \qquad \qquad (3') $
を満たす。
2)指数関数$f_{a}(x)=a^x$ は
$(0,\infty)$ から ${\bf R}$ の上への一対一で
連続な関数である。
(注) 2つの関数f、gに対して、その合成関数$(f\cdot g)$ は、
$(f\cdot g)(x)\triangleq f\bigl(g(x)\bigr)$ で定義される。
定理2
$a$ を 1と異なる正の実数とする。
すると
1) 任意の2つの正の実数b、cに対して,
$\qquad \log_{a}b + \log_{a}c = \log_{a}bc \qquad \qquad \qquad (4)$
2) 任意の2つの正の実数 b,c に対して,
$\qquad \log_{a}b - \log_{a}c = \log_{a}\frac{b}{c} \qquad \qquad \qquad (5)$
3) 任意の正の実数 b と任意の実数 c に対して
$\qquad \log_{a}b^c = c \log_{a}b \qquad \qquad \qquad (6)$
証明
1) 指数関数$f_{a}(x)=a^x$ の性質から、
$a^{x_{b}}= b,\quad a^{x_{c}}= c \qquad \qquad \qquad (7)$
を満たす、実数 $x_{b} \quad x_{c}$ がそれぞれ唯一つ定まる。
式(7)から対数関数の定義を用いると、
$\log_{a}b = x_{b} \quad \log_{a}c = x_{c}\qquad \qquad \qquad (8)$
すると、
$\quad \log_{a}b + \log_{a}c = x_b + x_c \quad (式(8)から)$
$=\log_{a} a^{x_b + x_c } \quad (式(1)から)$
$=\log_{a} (a^{x_b} a^{x_c }) \quad (指数関数の性質から)$
$=\log_{a}(bc) \quad (式(7)から) $
2)も同様に証明できる。
3)$X \triangleq \log_{a}b^c$ とおく。すると、対数の定義から、
$a^X = b^c$
$\qquad $ bは正の実数なので、$x_b=\log_{a}b とおくと、 a^{x_b}= b$なので、
$= (a^{x_b})^c = a^{x_b c} \quad (指数関数の性質から)$
故に
$a^X = a^{x_b c}$
指数関数が一対一関数なので、$X = x_b c = c \log_{a}b$
X の定義から、$\log_{a}b^c = c \log_{a}b \qquad \qquad \Box $
定理3 底の変換公式
任意の3つの正の実数 $a(\neq 1),b,c(\neq 1) $ に対して
$\qquad \log_{a}b = \frac{\log_{c}b}{\log_{c}a}\qquad \qquad \qquad (9)$
証明
定理1の式(3')から、
$ \quad a^{\log_{a}b} = b \qquad \qquad \qquad (10)$
底をcとする対数をとれば、
$\log_{c}a^{\log_{a}b} = \log_{c} b$
$\qquad $定理2の式(6)から、$\log_{c}a^{\log_{a}b} = (\log_{a}b)(\log_{c}a)$なので、
$ (\log_{a}b)(\log_{c}a) = \log_{c} b$
$a,\quad c$ は、1と異なる正の実数であるため、$ \log_{c}a \neq 0$ となり、
$\log_{a}b = \frac{\log_{c}b }{\log_{c}a}$
が得られた。
証明終わり。 $\qquad \qquad \qquad \Box $
対数関数
1と異なる正の実数 $a$ を考える。
指数関数 $f_{a}(x) = a^x$ は,命題2から、
${\bf R}$ から $(0,\infty)$ の上への、一対一、連続関数である。
すると、その逆関数$\quad (0,\infty) \ni a^x \to x \in {\bf R} $ が定義できる。
定義
$a$ を1と異なる正の実数とする。
$\log_{a} a^x \triangleq x \qquad \qquad \qquad (1)$
この関数を、$a$ を底とする対数関数とよぶ。
定理1
$a$ を 1と異なる正の実数とする。
1) $a$ を底とする対数関数 $\log_{a}$ は、
指数関数$f_{a}(x)=a^x$の逆関数であり、
$(\log_{a}\cdot f_{a})(x) = x \quad (x \in {\bf R})\qquad \qquad \qquad (2) $
すなわち、
$\log_{a}(a^x) = x \quad (x \in {\bf R})\qquad \qquad \qquad (2') $
と(注参照)、
$(f_{a}\cdot \log_{a})(y) = y \quad \bigl(y \in (0,\infty)\bigr)\qquad \qquad \qquad (3) $
すなわち、
$a^{\log_{a}(y)} = y \quad \bigl(y \in (0,\infty)\bigr)\qquad \qquad \qquad (3') $
を満たす。
2)指数関数$f_{a}(x)=a^x$ は
$(0,\infty)$ から ${\bf R}$ の上への一対一で
連続な関数である。
(注) 2つの関数f、gに対して、その合成関数$(f\cdot g)$ は、
$(f\cdot g)(x)\triangleq f\bigl(g(x)\bigr)$ で定義される。
定理2
$a$ を 1と異なる正の実数とする。
すると
1) 任意の2つの正の実数b、cに対して,
$\qquad \log_{a}b + \log_{a}c = \log_{a}bc \qquad \qquad \qquad (4)$
2) 任意の2つの正の実数 b,c に対して,
$\qquad \log_{a}b - \log_{a}c = \log_{a}\frac{b}{c} \qquad \qquad \qquad (5)$
3) 任意の正の実数 b と任意の実数 c に対して
$\qquad \log_{a}b^c = c \log_{a}b \qquad \qquad \qquad (6)$
証明
1) 指数関数$f_{a}(x)=a^x$ の性質から、
$a^{x_{b}}= b,\quad a^{x_{c}}= c \qquad \qquad \qquad (7)$
を満たす、実数 $x_{b} \quad x_{c}$ がそれぞれ唯一つ定まる。
式(7)から対数関数の定義を用いると、
$\log_{a}b = x_{b} \quad \log_{a}c = x_{c}\qquad \qquad \qquad (8)$
すると、
$\quad \log_{a}b + \log_{a}c = x_b + x_c \quad (式(8)から)$
$=\log_{a} a^{x_b + x_c } \quad (式(1)から)$
$=\log_{a} (a^{x_b} a^{x_c }) \quad (指数関数の性質から)$
$=\log_{a}(bc) \quad (式(7)から) $
2)も同様に証明できる。
3)$X \triangleq \log_{a}b^c$ とおく。すると、対数の定義から、
$a^X = b^c$
$\qquad $ bは正の実数なので、$x_b=\log_{a}b とおくと、 a^{x_b}= b$なので、
$= (a^{x_b})^c = a^{x_b c} \quad (指数関数の性質から)$
故に
$a^X = a^{x_b c}$
指数関数が一対一関数なので、$X = x_b c = c \log_{a}b$
X の定義から、$\log_{a}b^c = c \log_{a}b \qquad \qquad \Box $
定理3 底の変換公式
任意の3つの正の実数 $a(\neq 1),b,c(\neq 1) $ に対して
$\qquad \log_{a}b = \frac{\log_{c}b}{\log_{c}a}\qquad \qquad \qquad (9)$
証明
定理1の式(3')から、
$ \quad a^{\log_{a}b} = b \qquad \qquad \qquad (10)$
底をcとする対数をとれば、
$\log_{c}a^{\log_{a}b} = \log_{c} b$
$\qquad $定理2の式(6)から、$\log_{c}a^{\log_{a}b} = (\log_{a}b)(\log_{c}a)$なので、
$ (\log_{a}b)(\log_{c}a) = \log_{c} b$
$a,\quad c$ は、1と異なる正の実数であるため、$ \log_{c}a \neq 0$ となり、
$\log_{a}b = \frac{\log_{c}b }{\log_{c}a}$
が得られた。
証明終わり。 $\qquad \qquad \qquad \Box $