物理/質点の運動と質点系
提供: Internet Web School
目次 |
質点の運動と質点系
運動の3法則、万有引力の法則と力の法則を用いると、分子から銀河まであらゆる物体の運動を求めることが出来きる。
その正しさは地上の物体や人工衛星、惑星の運動などで確かめられている。
しかし、もっとはるかかなたの宇宙でもこれ等の法則は正しいのだろうか。
天体観測は、世界各地で行われ、年々新しい発見がされているが、現在のところ、この理論が間違っていることを示す観測結果は、得られていない。
そこで、これらの法則は宇宙の全体を支配しているものと、現在は信じられている。
運動の3法則からはエネルギー保存則や運動量保存則などの重要な保存則を導く事が出来る。
これらの保存則は、色々な運動を調べるとき、大変役立つ。これらについては次節で学ぶ。
質点の色々な運動
最初に最も簡単な運動から考える。
それは質点とみなせる物体の運動である。
質点の落体運動
地球上の物体は高いところから落とすと、時間とともに速度を増しながら落下する。
質点とみなせる物体の落下運動を、運動法則と力の法則を用いて、解析しよう。
質点の質量を$m$とすると、そこに作用する重力による力は、
真下(厳密には地球の重心;後で学ぶ)の方向・向きに大きさ$Mg$である。
落下の向きを負にした落下方向の一次元座標を考えると、重力加速度は$-g$で、質点$m$に作用する力は$-mg$である。
落下の加速度を$\alpha$と置くと、運動の第2法則より$m\alpha=-mg$.
ゆえに質点の落下加速度$\alpha$は負の重力加速度$-g$に等しい。
$t$で微分して$-g$となる関数は$-gt+c$なので、質点の速度は$-gt+c$である。
ここでcは定数で、初期時刻0における質点の速度であり、初期速度と呼ばれる。
微分して$-gt+c$となる関数を求めれば質点の位置$x(t)=-\frac{1}{2}gt^{2}+ ct + d$が得られる。
ここで、$d$は定数で初期時刻0での質点の位置(高さ)である。
これはガリレオが明らかにした落体法則である。
参考文献;
投射体の運動
質点を地面に対して角度$\theta$(ラジアン)、速さ$u$で投げたときの、質点はどのような運動を行うだろうか。
ガリレオは、慣性法則と落体の法則を組み合わせて利用して、放物線を描いて飛ぶことを発見した。
ニュートン力学を用いれば、運動の第2法則と質点に働く力(重力)から、以下のように、この運動を導ける。
適切な座標系をいれる
質点が投げ出された場所を原点とし、飛んでいく方向に地面と水平に引いた半直線をx軸の正の側に、地面と直角で上方に向かう半直線をy軸の正の側とする座標を定める。図参照。
質点に作用する力を求める
空気抵抗を無視すれば、質点に作用する力は、地球からの重力だけである。この力は、質点の質量を$M$,重力加速度を$g$とすると、質点の位置に関係なく常に、$\vec F=(o,-Mg)$である。
運動の第2法則から質点の運動方程式をつくる
質点の位置ベクトルを$\vec r=(x,y)$で表すと
運動方程式は、$M(d^2/dt^2)\vec{r(t)}=\vec F$である。
座標成分表示すると
$M(d^2/dt^2)x(t)=0$,$\quad$ $M(d^2/dt^2)y(t)=-Mg$
運動の初期状態の指定
投げ上げた瞬間を時刻$t=0$とおくと、質点の初期位置は$\vec{r}(0)=(0,0)$,$\quad$ 初期速度は$\vec{v}(0)=(u\cos{\theta},u\sin{\theta})$
運動方程式を初期状態を使って解く
(1)x成分の式を解く
$M(d^2/dt^2)x(t)=0$は、$M(d/dt)v_{x}(t)=0$なので$(d/dt)v_{x}(t)=0$。$\quad$ tで微分して零となるtの関数は定数なので$a$と書くと、$v_{x}(t)=a$
速度の定義より、$(d/dt)x(t)=v_{x}$なので、$(d/dt)x(t)=a$.$\quad$ $t$で微分して$a$となるのは$at+b$(bは未知定数)なので、$x(t)=at+b$
初期条件から、$a=v_{x}(0)=u\cos{\theta}$,$\quad$ また$x(0)=a0+b=0$なので$b=0$。
故に、$x(t)=(u\cos{\theta})t$
(2)y成分の式を解く
$M(d^2/dt^2)y(t)=-Mg$は、$(d/dt)v_{y}(t)=-g$ $\quad$ tで微分して$-g$となる関数は$-gt+c$(cは未知定数)なので、
$v_{y}(t)=-gt+c$ $\quad$故に$(d/dt)y(t)=-gt+c$
tで微分して$-gt+c$となる関数は、$-\frac{1}{2}gt^2+ct+d$なので、$y(t)=-\frac{1}{2}g^2t+ct+d$
初期速度の条件から、$c=-g0+c=v_{y}(0)=u\sin{\theta}$ $\quad$ $d=-\frac{1}{2}g0+c0+d=y(0)=0$
故に、$y(t)=-\frac{1}{2}gt^2+(u\sin{\theta})t$
(3)運動の軌跡(xとyとの関係式)を求める
$x(t)$の式から$t=x(t)/(u\cos{\theta})$
これを$y(t)=-\frac{1}{2}gt^2+(u\sin{\theta})t$に代入すると
$y(t)=(-g/2u^2\cos^2{\theta})x^2(t)+(\tan{\theta})x(t)$
これは上に凸な放物線である。
参考文献は
- ウィキブックス(高等学校理科 物理I 運動とエネルギー)の2.4.1 ニュートン方程式
惑星運動
前述のようにケプラーは、火星と太陽の観測データをユークリッド幾何学を巧みに利用して分析し次の惑星運動の3法則を発見した。
惑星運動の3法則を運動の第2法則と万有引力の法則から導く
この3法則は、運動の第2法則と万有引力の法則から導くことが出来るが少し難しい数学が必要である。大学で学ぶ。
惑星の軌道を太陽を中心とする円運動に限定すると、高校の数学の知識で3法則を導ける。
この場合ケプラーの第一法則は、仮定から、明白なので、第二法則から始める。
ケプラーの第2法則の導出
第二法則は、太陽と惑星を結ぶ動径の単位時間に掃く面積が一定であることを主張する。円運動のばあい、これは等速円運動であることと同じである。
そこで等速円運動であることを導こう。
太陽と惑星は質点として扱い、質量をそれぞれ$M,m$とする。
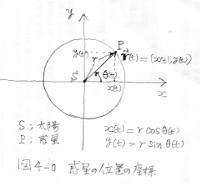
惑星の軌道面をxy平面にし、太陽をその原点にとる。円運動の半径を$r$, 太陽と時刻$t$における惑星を結ぶ線分が、x軸となす角度を$\theta =\theta(t)$とおく。
惑星Pの位置;$\vec{r}(t)=r(\cos\theta(t),\sin\theta(t))$
惑星の速度;$\vec{v}(t)=d\vec{r}(t)/dt=r(d\cos\theta(t)/dt,d\sin\theta(t)/dt)$
$=r(- \sin\theta(t)\frac{d\theta(t)}{dt},\cos\theta(t)\frac{d\theta(t)}{dt})$
=$ r \frac{d\theta(t)}{dt}(- \sin\theta(t), \cos\theta(t)) $
惑星の加速度;$\vec{\alpha}(t)=d\vec{v}(t)/dt=r(d^2\theta(t)/dt^2)(-\sin\theta(t),\cos\theta(t))$
$+r(d\theta(t)/dt)(-\cos\theta(t)\frac{ d\theta(t)}{dt},-\sin\theta(t)\frac{ d\theta(t)}{dt} )$
$= r(d^2\theta(t)/dt^2)(-\sin\theta(t),\cos\theta(t))-r( \frac{d\theta(t)}{dt})^2( \cos\theta(t), \sin\theta(t)) $
惑星に働く力;万有引力の法則より、太陽の方向に向いた、大きさ$GMm/r^2$の力なので
$\vec{F}(t)=-(GMm/r^2)(\cos\theta(t),\sin\theta(t))$
と表せる。
この力が、惑星の運動を変化させ、上述の加速度を生じさせたのだから、運動の第2法則$\quad m\vec{\alpha}(t)=\vec{F}(t)\quad$より、
$mr(d^2\theta(t)/dt^2)(-\sin\theta(t),\cos\theta(t))-mr( \frac{d\theta(t)}{dt})^2( \cos\theta(t), \sin\theta(t)$
$ =-(GMm/r^2)(\cos\theta(t),\sin\theta(t))$
変形すると、
$mr(d^2\theta(t)/dt^2)(-\sin\theta(t),\cos\theta(t))$
$ =(mr(\frac{d\theta(t)}{dt})^2-GMm/r^2)( \cos\theta(t), \sin\theta(t)) \qquad ------ \qquad (1)$
$(-\sin\theta(t),\cos\theta(t))$ と$( \cos\theta(t), \sin\theta(t))$は直交するベクトルなので、(1)式が成立する必要十分条件は、
$d^2\theta(t)/dt^2=0 \qquad ------ \qquad (2)$,
$mr(\frac{d\theta(t)}{dt})^2-GMm/r^2=0 \qquad ------ \qquad (3)$
である。
(2)式から、角速度$\omega(t)=\frac{d\theta(t)}{dt}=\omega_{0}$(定数)が
(3)式から、$mr(\frac{d\theta(t)}{dt})^2=GMm/r^2$が
得られる。
これらより、惑星は等角速度
$\Large{\omega_{0}=\pm\sqrt{GM/r^3}}$ $\qquad ------ \qquad $ (4)
で太陽の周りを回転することが分かり、ケプラーの第2法則が得られた。
ケプラーの第3法則の導出
惑星が太陽の周りを一周する時間$T$(周期という)は、$T=2\pi/\omega_0$なので、(4)式より、
$T=2\pi/\sqrt{GM/r^3}=2\pi\sqrt{r^3/GM}$,
故に$T^2=4\pi^2r^3/GM$,
$T^2/r^3=4\pi^2/GM$
これは軌道が円の場合のケプラーの第3法則である。
万有引力の法則を,ケプラーの法則と運動の第2法則から導く
惑星が太陽の周りを円運動しているとき、太陽が惑星に及ぼしている力を計算する。
ケプラーの第2法則より、円運動する惑星は角速度一定である。これを$\omega_0$とする。
太陽の位置を原点とし円の半径を$r$とすると、この惑星の加速度は$\vec{\alpha}(t)=-r( d\theta(t)/dt)^2( \cos\theta(t), \sin\theta(t)) =-r\omega_0^2( \cos\theta(t), \sin\theta(t))$ 。これは、太陽にむかう大きさ$r\omega_0^2$のベクトル。
運動の第2法則より、惑星に働く力$\vec F$は、太陽の方向に、大きさ$mr\omega_0^2$
ここで、$m$ は惑星の慣性質量である。
$\omega_0^2$を$r$の関数で表すためケプラーの第3法則と用いる。
惑星の公転周期$T$と円の半径$r$の間には$T^2/r^3=C,\quad C$;定数
$T=2\pi/\omega_0$なので
$(2\pi/\omega_0)^2/r^3=C \quad $∴$\omega_0^2=4\pi^2/(Cr^{3})$
それゆえ、力の大きさは
$mr\omega_0^2=\frac{4\pi^2}{C} \frac{m}{r^2}$
さらに、太陽の質量$M$が$k$倍になると、質量$M$の太陽が$k$個あり、それぞれが惑星に上記の力を与えると考えられる。
すると惑星に働く力は$k$倍になるので力の比例部分$\frac{4\pi^2}{C}$は太陽の質量$M$に比例することが分かる。
比例定数を$G$とおくと、$\frac{4\pi^2}{C}=GM$
従って惑星に働く力の大きさは、太陽の方向に、
$GM\frac{m}{r^2}=G\frac{mM}{r^2}$
これは万有引力の法則である。
(注)この式は万有引力の法則の式と同じだが、質量$m$は、慣性質量であり、対称性から太陽の質量$M$も慣性質量と考えられる。
しかしニュートンは重力を生む質量は、慣性質量と完全には一致しない可能性もあると考え、重力質量という概念を生みだしと思われる。
既述のように、多くの実験の結果、両質量は同一であると考えられている。
重量質量を使わず、慣性質量だけを用いても、ニュートン力学を構成することが出来る。これを提唱する物理学者もいる。
それには万有引力の法則のかわりに、次の法則を採用すればよい。
外力が働かないときは、どんな2質点も、お互いに相手に向かって,
加速度運動して近ずく。両者の加速度は、両者の距離の2乗$r^2$に反比例し、それぞれの慣性質量の比に反比例する。
式で書くと、
質点1の慣性質量と加速度の大きさを$m_1$,$\alpha_1$
質点2の慣性質量と加速度の大きさを$m_2$,$\alpha_2$
とすると、$m_1\alpha_1=m_2\alpha_2$、$m_1\propto 1/r^2$,$m_2 \propto 1/r^2$
この法則と運動法則により2質点間に働く力(万有引力)を求めると、
ニュートンの万有引力の法則と同じ式だが、質量は慣性質量になり、
重量質量を用いずニュートン力学が構成できる。
振り子と単振動
- ウィキペディア(単振動)の「振り子」の項を見てください。
質点のつり合い
質点に力F1,,Fnが作用し、質点が静止したまま(あるいは等速直線運動)であるとき、それらの力は釣り合っているという。
釣り合いの条件は、F1+ +Fn=0です(運動の第2法則と力の合成則から導出できる)。
質点系の運動
2個以上の質点が集まって出来ている系を質点系という。
質点系というときは、各質点は密集していても、離れ離れでも良い。互いに固着しようが、自由に動けようが構わない。
すべての物質は、分子の集合と考えたり、細分化して極小部分に分け、それらの集合と考えれば、十分な精度で、質点系とみなすことができる。
そのため質点系の運動の法則を、ニュートンの運動法則から導出すれば、その応用範囲は非常に広い。
質点系の運動と重心
系の任意の2つの質点間には相互に及ぼしあう力が働いていてもよい。
この相互作用力は作用・反作用の法則から、
大きさと方向は同じで向きは逆である。
この力を質点系の”内力”という。
質点系の各質点に外部から力(外力という)が加わる時、この質点系はどんな運動をするだろうか。
質点系の各質点の位置を$\vec{r_i}$、質量を$m_i $とし、
質点$m_i$ に作用する外力を$\vec{f_i}$、
$m_i$ に、他の質点$m_j $から作用する内力を$\vec{f_{ij}}$とする($i,j=1 \ldots N$)。
すると、各質点に対して、運動の第2法則により、
$\frac{d}{dt} (m_i \vec{v_i})=\vec{f_i}+\sum_{j\neq i}\vec{f_{ij}} $ $\qquad$ ここで$\vec{v_i}=d\vec{r_i}/dt$、
各ベクトルを自由ベクトルとみなして$i=1 \ldots N$について加え合わせると、
$\frac{d^2}{dt^2} \sum_i{ m_i \vec{r_i}}
=\sum_i\frac{d}{dt} { m_i \vec{v_i}}
=\sum_i{\vec{f_i}}+\sum_{i}\sum_{j\neq i}\vec{f_{ij}} $
$=\sum_i{\vec{f_i}}+\sum_{i<j}\vec{f_{ij}} +\sum_{j<i}\vec{f_{ij}}$
上の式の第3項の変数名iとjを入れ替えると
$=\sum_i{\vec{f_i}}+\sum_{i<j}\vec{f_{ij}} +\sum_{i<j}\vec{f_{ji}}$
剛体の内力についての仮定から、$\vec{f_{ji}}=-\vec{f_{ij}}$なので、
$=\sum_i{\vec{f_i}}+\sum_{i<j}(\vec{f_{ij}} -\vec{f_{ij}})=\sum_i{\vec{f_i}}$
故に、
$\frac{d^2}{dt^2} \sum_i{ m_i \vec{r_i}} =\sum_i{\vec{f_i}} $
が得られる。
質点系の全質量$M= \sum_i{m_i} $と質点系に働く全外力$\vec{F}= \sum_i{\vec{f_i}} $を用いて書きなおすと、
$M\frac{d^2}{dt^2}(\sum_i\frac{ m_i \vec{r_i}}{M})= \vec{F} $
質点系の重心$\vec{R}$を $\quad \vec{R}=\sum_i\frac{ m_i \vec{r_i}}{M }$ で定義すると、
$M\frac{d^2}{dt^2}\vec R= \vec{F} $
この式は、力$\vec{F}$をうける質量$M$の質点の運動方程式と同じである。
以下の解説も参考にしてください。
複雑にみえる運動も重心の運動をみれば簡単である
体操選手の運動は、跳躍などで空中をまいながら、回転や体の屈伸、ひねりなどを行う。大変複雑で美しい。
しかし、導出した質点系の重心の運動法則から、体の重心の運動は、投射体の運動であり、放物線をえがいて移動することが分かる。
空中に飛び出た瞬間の重心の位置と速度(速さと方向・向き)で、その軌跡は完全に決まってしまうのである。
複雑さ・美しさは、重心周りの体の姿勢・ひねりとその変化、それに伴う重心周りの回転変化によって、もたらされる。
回転運動については、
[|「2.5 剛体と回転力」]と
[|「2.6 剛体の回転運動と釣合い」]で調べる。
ガリレイ変換とガリレイの相対性原理
どのような慣性座標系で観測しても力学の法則は同じであるという原理。
一つの慣性系にたいして等速度並進運動(注)する観測系を考えると、
力の働いてない物体はやはり、等速度運動するので慣性系であり、
運動の第2、第3法則、万有引力の法則、力の合成則が成立することを主張している。
(注) 座標系$S'(O'-x'_{1}x'_{2}x'_{3})$の任意の点$(x'_1,x'_2,x'_3)$が、
座標系$S(O-x_{1}x_{2}x_{3})$からみると、
すべて同じ速度($\frac{d\vec{OO'}}{dt}(t)$で移動すること。
言い換えると、S'系の各座標軸上の点(1,0,0),(0,1,0),(0,0,1)が、
S系からみると皆、同じ速度($\frac{d\vec{OO'}}{dt}(t)$で移動すること。
重要な原理なので、詳しく考察しよう。
ガリレイ変換
観測座標系$S(O-x_{1}x_{2}x_{3})$からみて、観測座標系$S'(O'-x'_{1}x'_{2}x'_{3})$が
並進運動しているとする。
ニュートン力学での時間・空間とガリレイ変換
ニュートン力学では
時間は全ての観測系で同一であると考える(絶対時間の存在)。
空間の任意の点Pを、
ある時刻tで座標系S,S'から観測したときの位置ベクトルを、それぞれ$\vec r,\vec{r'}$とする。
ニュートン力学では
空間の点Pから、他の点Qに向けた有向線分$\vec{PQ}$は、
どの観測系からみても、同一であると考える(空間の均質性)。
するとS'系で観測した、点O'から点Pまでの有向線分$\vec{r'}$は、
S系で観測するO'から点Pまでの有向線分でもある。
このようにみなして、S系での有向線分の和をとると、
$\vec{r}=\vec{OO'}(t)+\vec{r'}\qquad \qquad (1)$
図参照のこと。
式(1)を、S系とS'系の観測値を関係づける、ガリレイ変換と呼ぶ。
次にある質点mの運動を観測する。
時刻tにおいて質点を、
互いに並進運動する2つの系S,S'から見たときの位置ベクトルを、それぞれ、
$\vec{r}=\vec{r}(t)$、$\vec{r'}=\vec{r'}(t)$と書く。
これらの位置ベクトルの関係は、式(1)から、
$\vec{r}(t)=\vec{OO'}(t)+\vec{r'}(t) \qquad \qquad (2)$
両辺をtで微分すると、両系からみた、速度の関係式
$\vec{v}(t)=\frac{\vec{OO'(t)}}{dt}+\vec{v'}(t) \qquad \qquad (2')$
が得られる。
命題
もしS'系がS系からみて速度$\vec u$で等速度運動しているならば
(1)$\vec{v}(t)=\vec u+\vec{v'}(t) $
(2)両系から観測した加速度は等しい。記号で書くと$\vec{\alpha}(t)=\vec{{\alpha}'}(t) $
何故ならば、(1)は、$\frac{\vec{OO'(t)}}{dt}=\vec u$なので、式(2')から明らか。
(2)は$\vec{v}(t)=\vec u+\vec{v'}(t) $をtで微分すれば良い。
☆☆ ガリレイ変換の座標表示
S'座標系$O'-x'_{1}x'_{2}x'_{3}$の座標軸が、
S系の対応する座標軸と平行を保ちながら並進運動する場合には、
ガリレイ変換式(2)は、座標成分表示(注参照)できる。
(注)ベクトルの座標成分表示(詳しくは「2.1.2 質点の運動を数式で表すにはどうするか?」を参照)
「2.1.2 」節で説明したように、
$x_{i}$軸上の、長さ1で正方向のベクトルを$\vec{e}_i$と書き、Sの第i基底という。
任意のベクトル$\vec r$は,この基底を用いて、
$\vec r=\sum_{i=1}^{3}r_{i}\vec{e}_i$
と表せる。
ここで、$r_{i}:=\vec{r} \cdot \vec{e}_i$は、
位置ベクトル$\vec r$の点から、第i直交軸に下ろした垂線の足の座標である。
図参照。
$(r_1,r_2,r_3)$をベクトル$\vec r$の座標成分表示と呼ぶ。
同様に、座標系S'の第i基底$\vec{e'}_i$が定義でき、
S'系の任意のベクトル$\vec r'$は
$\vec r'=\sum_{i=1}^{3}r'_{i}\vec{e'}_i$
と表せる。
注の終わり。
両系の対応する座標軸が平行と仮定しているので
対応する基底は長さと方向・向きが等しくなり、ベクトルとして一致する。
$\vec{e}_i=\vec{e'}_i,\quad (i=1,2,3)$
すると次の命題が成り立つ。
命題1
系SとS'の各座標系が平行とする。
ガリレイ変換式(2)における、
$\vec{r}(t)$の座標成分を、$(r_{1}(t),r_{2}(t),r_{3}(t))$
$\vec{r'}(t)$の座標成分を、$(r'_{1}(t),r'_{2}(t),r'_{3}(t))$
$\vec{OO'}(t)$の(S座標系からみた)座標成分を、$(O'_{1}(t),O'_{2}(t),O'_{3}(t))$
とする。このときガリレイ変換(2)は
$r_{i}(t)=O'_{i}(t)+r_{i}(t)、 \quad (i=1,2,3)$
証明
座標表示の定義から、
$\vec{r}(t)=\sum_{i=1}^{3}r_{i}(t)\vec{e}_i$
$\vec{OO'}(t)=\sum_{i=1}^{3}O'_{i}(t)\vec{e}_i$
$\vec{r'}(t)=\sum_{i=1}^{3}r'_{i}(t)\vec{e'}_i$
命題の仮定から、$\vec{e}_i=\vec{e'}_i,\quad (i=1,2,3)$なので
$\vec{r'}(t)=\sum_{i=1}^{3}r'_{i}(t)\vec{e}_i$
これらの式を、ガリレイ変換式、
$\vec{r}(t)=\vec{OO'}(t)+\vec{r'}(t) \qquad \qquad (2)$
に代入して
$\sum_{i=1}^{3}r_{i}(t)\vec{e}_i
=\sum_{i=1}^{3}O'_{i}(t)\vec{e}_i +\sum_{i=1}^{3}r'_{i}(t)\vec{e}_i$
$=\sum_{i=1}^{3}(O'_{i}(t)+r'_{i}(t))\vec{e}_i$
座標表示は唯一つしかないので、上式の左辺と右辺を比較して
$r_{i}(t)=O'_{i}(t)+r'_{i}(t),(i=1,2,3)$
を得る。証明終わり。
☆☆ 2質点の相対的位置と相対速度は、観測系によらず一定
SとS'を、それぞれ原点をOとO'とする観測系とする。
時刻tに質点$m_{1}$を、
Oからみた位置ベクトルを$\vec{r^1}(t)$、
O'からみた位置ベクトルを$\vec{r'^1}(t)$
時刻tに質点$m_{2}$を、
両系からみた位置ベクトルを$\vec{r^1}(t)$、$\vec{r'^1}(t)$とする。
すると次の命題が成り立つ。
命題2
$\vec{r^{2}}(t)-\vec{r^{1}}(t)=\vec{r'^{2}}(t)-\vec{r'^{1}}(t)$
$\vec{v^{2}}(t)-\vec{v^{1}}(t)=\vec{v'^{2}}(t)-\vec{v'^{1}}(t)$
ここでrとvはS系からみた質点の位置と速度、r'とv'はS'系からみた質点の速度である。
さらにOを原点とする座標系$S(O-x_{1}x_{2}x_{3})$と、
それと平行な座標軸をもつO'を原点とする座標系$S'(O'-x'_{1}x'_{2}x'_{3})$を
定めると,上の式は座標成分表示でき、
${r^{2}_i}(t)-{r^{1}_i}(t)={r'^{2}_i}(t)-{r'^{1}_i}(t),\qquad (i=1,2,3)$
証明
ガリレイ変換式(2)より、
$\vec{r^{2}}-\vec{r^{1}}
=(\vec{OO'}+\vec{r'^{2}})-(\vec{OO'}+\vec{r^{1}})
=\vec{r'^2}-\vec{r'^1}$
後半の証明は、命題1と同じようにできるので省略する。
補題の証明終わり。
☆☆ 観測座標系が慣性系となる条件
命題3
慣性座標系$S(O-x_{1}x_{2}x_{3})$と、
同じ原点を持つ座標系$S'(O-x'_{1}x'_{2}x'_{3})$を考える。
このとき、
座標系S'が慣性系になる必要十分条件は
S'の3つの座標軸が、時間が経過してもS系からみると動かないこと。
証明:
(=>)S'が慣性系とする。
S'系の座標軸が時間とともに動くこともあると仮定すると矛盾が起きることを示そう。
慣性系Sからみて原点以外の場所に静止している質点を考える。
位置ベクトルを$\vec r$とする。
この質点に働く力は零であり、自由運動である。
どの慣性系からみても自由運動は等速度運動に見えるので、
この質点を慣性系S'でみても、等速度運動をする。
他方、S'系の座標軸が動くとすると、原点はOに固定されているので、
原点周りの回転をすることになる。
回転していく座標からS系で静止している質点の位置を観測すると、
位置ベクトルは長さを変えず、移動して見える。
すなわち、原点Oを中心とする半径$\|\vec r\|$の球面状を移動する。図参照
これは等速度運動(直線運動になる)と矛盾する。
(<=)
S'の3つの座標軸が、時間が経過してもS系からみると動かないとする。
すると、$S'(O-x'_{1}x'_{2}x'_{3})$の基底$\vec{e'}_i,\quad (i=1,2,3)$は
時不変のベクトルになる。
このとき、自由運動する質点の運動が、S'系からみても等速度運動になることを示せばよい。
この質点を慣性系Sから観測すれば、等速度運動をするので、
質点の位置ベクトル$\vec{r}(t)$は、
$\frac{d\vec r}{dt}(t)=\vec v=constant$(等速度)
これを、S'系から観測すると、その位置ベクトルと速度ベクトルは、
$O=O'$なのでガリレイ変換式により、
$\vec{r}(t)=\vec{r'}(t) $
両辺を時間で微分して、
$\vec{v}(t)=\vec{v'}(t) =\vec v$
S'系の座標軸は時不変なので、速度ベクトル$\vec v$の座標成分
$\vec v \cdot \vec{e'}_i \quad $(i=1,2,3)
は一定値になり、等速度運動になる。証明終わり。
命題4
S系(原点O)は慣性系とし、
S'系(原点O')はS系からみて原点O'が等速度で並進運動をする。
このとき、S'系は慣性系である。
証明;
仮定から、$\frac{\vec{OO'}}{dt}(t)=\vec{w} )$と書ける。
自由運動がS'系からみても等速直線運動になることを示せば良い。
慣性系Sからみた自由運動$\vec{r}(t)$は等速直線運動になる。
そこで、ある速度ベクトル$\vec{v}$を用いて$\vec v(t)=\frac{dr}{dt}(t)=\vec{v}$と書ける。
ガリレイ変換式
$\vec{r}(t)=\vec{OO'}(t)+\vec{r'}(t) $
の両辺を時間tで微分すると
$\vec{v}=\vec{w}+\vec v'(t) $
移項すると、
$\vec v'(t)=\vec{v}-\vec{w}$
S’系は並進運動するのでその座標の3つの基底は時間が経過しても不変なので、
、速度$\vec{v}-\vec{w}$の座標成分は一定値になる。
自由運動する質点は座標系S'からみても速度一定であることが示せた。証明終わり。
命題4の逆命題も成り立つ。
命題5
慣性座標系$S(O-x_{1}x_{2}x_{3})$と、
座標系$S'(O'-x'_{1}x'_{2}x'_{3})$を考える。
もしS'が慣性系ならば、
S'系の原点O'は系Sで観測すると等速度で、S'は並進運動をする。
証明:
自由運動する質点は、どちらの系S,S'からみても、等速直線運動する。
そこで、それらの速度をそれぞれ
$\vec v=\frac{dr}{dt}(t)\quad $,$\vec{v'}=\frac{dr'}{dt}(t)$と書く。
ガリレイ変換式(2)の両辺を時間tで微分すると、
$\vec{v}=\frac{\vec{OO'}}{dt}(t)+\vec{v'}$
移項すると、
$\frac{\vec{OO'}}{dt}(t)=\vec{v'}-\vec{v}$
ゆえに、O'はS系からみて、等速直線運動する。
次にS'系は並進運動であることを示す。
S'系が並進運動していないとする。
S’系の原点O’を原点とし、並進運動する座標系$\tilde{S}(O'-\tilde{x}_1 \tilde{x}_2 \tilde{x}_3)$をとる。
すると$\tilde{S}$系は、命題4から、慣性系になる。
この慣性系からみると、S'系は原点が同じで、その座標系が時間とともに回転する。
すると命題3により、S'系は、慣性系にはなりえない。
これはS'が慣性系であることと矛盾する。したがってS'は並進運動することが示せた。証明終わり。
命題6
慣性座標系SとS'を考える。
運動する質点の加速度は、どちらの系で観測してもベクトルとして同一である。
両方の座標系が平行ならば、座標成分も等しくなる。
証明;
命題5から
S'系は、S系からみて、ある速度$\vec{w}$で、等速度並進運動する。
すると、ガリレイ変換の式$\vec{r}(t)=\vec{OO'}(t)+\vec{r'}(t)$の両辺を
tで微分して
$\vec{v}(t)=\vec{w}+\vec v'(t) $
この式の両辺をtで微分すれば、
$\vec{\alpha}(t)=\vec{\alpha'}(t) $
2つの座標系が平行の場合、両者の基底は、ベクトルとして同一になり、
$\vec{\alpha}(t),\vec{\alpha'}(t) $の座標成分表示も等しくなる。
☆☆ ガリレイの相対性原理の証明
力学の第一法則(慣性法則)により、この宇宙には慣性系は存在する。
実際、太陽系の重心を原点にし、遠方の恒星で座標系を決めれば、
これが慣性系Sになることが経験的に確かめられている。
この慣性系では、多くの経験や実験から、
力学の基本法則(力の合成則と運動の第2法則、第3法則、万有引力の法則)
が成立するとすることが判明している。
このとき、ガリレイの相対性原理は、
全ての慣性系で、力学の基本法則が成立する
と主張する。
この原理は、
2つの慣性系からの位置の観測値の間にガリレイ変換の関係が成り立ち、
質量と力の観測値が、どの慣性系からみても同じならば、
次のように証明できる。
慣性系Sで、力学の基本法則がすべて成立すると仮定する。
(1)。S'系で、運動の第2法則は成り立つことを示す。
力$\vec F$が作用して、質点mが運動しているとする。
S系で、運動の第2法則は成り立つので、
$\vec F=m\alpha:=m\frac{d\vec v}{dt}(t)$
命題6から、S系で観測した加速度$\alpha$は、S'系で観測した加速度$\alpha'$に等しい。
ゆえに、
$\vec F=m\alpha'$
mとFは、仮定により、S'系で観測した質点の質量とそれに作用する力でもあるので、
S'系でも運動の第2法則が成り立つことが示せた。
(2)。力の合成法則がS'系でも成立。
質点mに、n個の力$\vec{F}_i,(i=1,2,,,n)$が同時に作用しているとする。
S系では、力の合成法則がなりたつので、
質点はひとつの合力$\vec F:=\sum_{i=1}^{n}\vec{F}_i$を受けた質点mと同じく
$\vec F=m\alpha$
に従って運動する。
ところが、この質点の加速度をS'から観測しても変わらないので
$\vec F=m\alpha'$
質量と力は慣性系によらず一定なので、
mと$\vec F$は、S'系で観測した質点の質量と合力でもある。
したがって、S'系でも、n個の力が同時に作用する質点の運動は、
それらの合力が作用する運動と同一になる。力の合成則が示せた。
(3)。力は両系で共通なので明らかにS'系でも作用反作用の法則(第3法則)が成立。
(4)。万有引力の法則がS'系で成立する。
命題2から、
2つの質点$m_{1},m_{2}$を、観測系SとS'から観測すると、
$\vec{r_{2}}(t)-\vec{r_{1}}(t)=\vec{r'_{2}}(t)-\vec{r'_{1}}(t)$
この関係と質量不変、力の不変の性質から、S系で成立する万有引力の法則の式は、
S'系の万有引力の法則の式になっていることが分かる。
☆☆ ガリレイの相対性原理から質量と力の不変性を導く
前節では、2つの慣性系の位置ベクトルの間にガリレイ変換の関係が成り立つとき、
質量と力が慣性系の取り方によらずに決まるならば、相対性原理が成立することを示した。
この節では、逆にガリレイの相対性原理から、
質量と力が慣性座標系に依存しないことを示そう。
☆☆ 作用する力を質量で割ったものは、どの慣性系からみても同一
2つの慣性系S,S'をとる。原点をそれぞれO,O'とする。
前項で証明したように、
ある速度ベクトル$\vec{v}$が存在して、$\frac{d\vec{OO'}}{dt}(t)=\vec{v}$
質点に力が作用し、運動するのを、2つの慣性系S,S'から観測する。
系Sからみた質点の質量をm、作用する力を$\vec F$とする。
すると運動の第2法則から$m\frac {dv}{dt}(t)=\vec F$
ゆえに、$\frac {dv}{dt}(t)=\vec F/m \qquad \qquad (1)$
同様に、系S'からみた質点の質量を$m'$、作用する力を$\vec F'$とすると
$\frac {dv'}{dt}(t)=\vec F'/m'\qquad \qquad (2)$
命題3から$\frac {dv}{dt}(t)= \frac {dv'}{dt}(t)|\qquad \qquad (3)$
式(1)(2)(3)から
$\vec F/m=\frac {dv}{dt}(t)=\frac {dv'}{dt}(t)=\vec F'/m'\qquad \qquad (4)$
所望の結論が得られた。
☆☆ 質量は、どの慣性系からみても同一
2つの質点が万有引力で引き合って、運動しているのを、系SとS'から観測する。
S系の観測値は、2つの質点の質量が$m_1,m_2$,位置ベクトルが$\vec r_{1},\vec r_{2}$、
S'系の観測値は、質量$m'_1,m'_2$,位置ベクトル$\vec r'_{1},\vec r'_{2}$
であるとする。
第1の質点が第2の質点から受ける万有引力は、S系では、
$\vec{F_{1,2}}=G\frac{m_{1}m_{2}}{\|\vec{r_2}-\vec{r_1}\|^2}
\frac{\vec{r_2}-\vec{r_1}}{\|\vec{r_2}-\vec{r_1}\|}$
同じくS'では、
$\vec{F'_{1,2}}=G\frac{m'_{1}m'_{2}}{\|\vec{r'_2}-\vec{r'_1}\|^2}
\frac{\vec{r'_2}-\vec{r'_1}}{\|\vec{r'_2}-\vec{r'_1}\|}$
前項で証明した式(4)により
$\vec F_{1,2}/m_{1}=\vec F'_{1,2}/m'_{1}$なので、上の式から
$G\frac{m_{2}}{\|\vec{r_2}-\vec{r_1}\|^2}
\frac{\vec{r_2}-\vec{r_1}}{\|\vec{r_2}-\vec{r_1}\|}
=G\frac{m'_{2}}{\|\vec{r'_2}-\vec{r'_1}\|^2}
\frac{\vec{r'_2}-\vec{r'_1}}{\|\vec{r'_2}-\vec{r'_1}\|}\qquad \qquad (5)$
ガリレイ変換の節の命題1により、
$\vec{r_2}-\vec{r_1}=\vec{r'_2}-\vec{r'_1}$なので式(5)から
$m_{2}=m'_{2}$
同様にして、第2の質点が第1の質点から受ける万有引力の式から、$m_{1}=m'_{1}$
所望の結論が得られた。
☆☆力はどの慣性系からみても同一
$\vec F/m= F'/m'\qquad \qquad (4)$
と$m= m'$から、明らか。
ガリレイの相対性原理の余話
ガリレイの相対性原理は、
力学だけでなく、古典力学のすべての領域で成立するという原理に拡張され、
長い間物理学の指導原理となっていた。
ところが電磁気学の基本法則のマクスウェル方程式は、
ガリレイ変換で、形をかえてしまい、相対性原理は成立しない。
マクスウェル方程式が正しければ、
ガリレイの相対性原理やその根底にあるニュートン力学的世界観が
現実には成立しないことになるので大きな問題になった。
20世紀になって、この原理はアインシュタインによって修正された。
これについては本テキストでは扱わない。
仕事
物体に力を加えて動かす時、力はこの物体に仕事をするという。
仕事(の量)は力の大きさと動かした距離の積に比例する。
正確には、加えられる力$\vec F$ が一定で、
力の向きに対して角度$\theta$[rad] だけ傾いている直線上を $\vec s$ 移動したとき、
仕事W は、
$W=\|\vec F\|\|\vec s\| \cos\theta$
で定義する。
ここで任意のヴェクトル$\vec a$に対して、$\|\vec{a}\|$はその大きさ$\sqrt{\sum_{i}a_i^2}$を表す。
特に、この式において$\theta=0$(すなわち $\cos\theta = 1$)とすると
「加えられる力が一定であり力の方向が運動の方向と一致している場合」になり、
$W=\|\vec F\|\|\vec s\| $ である。
また、$\theta=\pi/2$($\cos\theta = 0$)のとき、$W = 0$となる。
すなわち、力が運動の方向と直角方向にはたらいている場合、その力は仕事をしない。
$W=\|\vec F\|(\|\vec s\| \cos\theta)$と表現すると、
仕事は、力の方向に$\|\vec s\| \cos\theta$だけ動かしたときの仕事に等しいことが分かる。
$W=(\|\vec F\| \cos\theta)\|\vec s\|$と表現すると、
仕事は、
大きさ$\|\vec F\| \cos\theta$ の$\vec s$方向の力(力$\vec F$の$\vec s$方向成分)を加えて、
$\vec s$だけ動かしたときの仕事に等しいことが分かる。
- ウィキペディア(仕事)を参照のこと。
仕事の内積を用いた表現
内積は、仕事の記述や計算に便利な数学の概念である。
内積の定義と仕事の内積表現
ベクトル$\vec a,\vec b$の内積$ \vec a \cdot \vec b $は、$\|\vec{a}\|\|\vec{b}\|
\cos\theta$で定義する。
ここで、$\theta$は、ベクトル$\vec a,\vec b$のなす角($0\le \theta \le \pi$ )である。
- ウィキブックス(高等学校数学B ベクトル) の1.1.6~ 1.1.8を参照のこと。
ウィキブックスでは2次元のベクトルを中心にして説明しているが、
3次元ベクトルの場合にも、成り立つように修正することは容易である。
例えば、ベクトル$\vec a = (a _1,a _2,a_3)$の長さは、$\|\vec a\|= \sqrt {a _1^2 +a _2^2+a _3^2}$,
ベクトルの内積は、この長さを使えば、全く同じ式で良い。
内積を使った 仕事の表現
内積 $\cdot $を用いると、
物体に力$\vec{F}$を加えて、$\vec{PQ}$(P点からQ点まで)動かした時の力のなす仕事は、
$ W=\vec{F}\cdot\vec{PQ} $と表せる。
内積の性質
仕事は前述のように内積で表現できるので、
内積の性質を調べておくと、仕事について考察する時に役立つ。
以下では、
$\vec a,\vec b,\vec c$は、すべて同じ次元(2か3)のベクトルとし、 $\alpha$は実数とする。
座標成分表示が必要な命題では、直交座標系表示を用いる。
(1)$\vec a \cdot \vec b =\vec b \cdot \vec a$
(2)$\vec a \cdot \vec b =\sum_{i}a_ib_i$ 、
ここで$a_1,b_1$はそれぞれ$\vec a,\vec b$のx座標成分、同様に、添え字2はy座標成分、3はz座標成分
直交座標系はどんなものでも良い。しかしすべてのベクトルは同じ座標系で座標成分表示しなければならない。
(3)$(\vec a +\vec b) \cdot \vec c =\vec a \cdot \vec c+\vec b \cdot \vec c$
$\vec a \cdot(\vec b+\vec c) =\vec a \cdot \vec b+\vec a \cdot \vec c$
(4)$(\alpha \vec a)\cdot \vec b =\vec a \cdot (\alpha \vec b)=\alpha (\vec a \cdot \vec b)$
が成り立つ。
(5)$\|\vec a \cdot \vec b\| \leq \|\vec a\|\|\vec b\|$
(6)ノルムの性質;$\|\vec a + \vec b\| \leq \|\vec a\| + \|\vec b\|$
証明は、本テキストの「8章 物理数学の8.1平面と空間のベクトル」にある。
力が変動したり、物体の移動が曲線であるときの仕事
物体に作用する万有引力は、
物体の位置により決まる。
力の場
質点がどこにあろうが、
その位置$\vec x$に応じて力$\vec{F}(\vec x)$が作用する空間を力の場という。
万有引力は位置$\vec x$についての連続なベクトル値関数である。
力の場の力のおこなう仕事の近似値
この力を受けて運動する物体は曲線を描いて運動することが多い(彗星、惑星の運動など)。
物体がさまざまな理由で運動を拘束され曲線を描いて動くときもある。
こうした場合、力のなす仕事をどのように決めたらよいだろうか。
運動の軌跡(向きつき曲線C)を、細かく区切って
n個の向きつき小曲線部分${C^n}_i$に分ける(i=1,2,,,n)。
各小部分${C^n}_i$の両端の位置ベクトルを、${\vec{x}^n}_{i-1},{\vec{x}^n}_i$と書く。図参照のこと。
この分割に名前を付け$\Delta^n =\{{C^n}_i \mid i=1,2,,,n\}$と書く。
nを増やして分割を細かくすると、
連続的に変化する力は、各小部分${C^n}_i$上でほぼ一定となる。
${C^n}_i$の形状もほぼ線分とみなせるようになる。
そこで、i番目の小部分上の一点${\xi}^{n}_i$を選び、
この小部分上では、力を$\vec{F}({\xi}^{n}_i)$で近似する。
また、i番目の小部分を向きつき線分
${\vec{x}^n}_i-{\vec{x}^n}_{i-1}$
で近似する。
すると、この小部分の移動で力の行う仕事は
$ W_{i}({\Delta}^n,{\xi}^{n}_i)
=\vec{F}({\xi}^{n}_i)\cdot ({\vec{x}^n}_i-{\vec{x}^n}_{i-1})$
で近似できる。
これをすべて加えた
$W({\Delta}^n,\{{\xi}^{n}_i\}_{i=1}^{n})
=\sum_{i=1}^{n}W_{i}({\Delta}^n,{\xi}^{n}_i) $
$=\sum_{i=1}^{n}\vec{F}({\xi}^{n}_i)\cdot ({\vec{x}^n}_i-{\vec{x}^n}_{i-1})\qquad (1)$
は、力のなした仕事の近似値を与えると考えられる。
線積分可能性の定義
ある数Wが存在して、
分割数nをどんどん増やし、小部分の長さを零に近づくて行く。
この時、分割の仕方$\Delta^n$や$\{{\xi}^{n}_i\}_{i=1}^{n}$の選び方によらず
$W=\lim_{n\to \infty}W({\Delta}^n, \{{\xi}^{n}_i\}_{i=1}^{n})$
となるとき、
ベクトル値関数$\vec{F}(\vec x)$は、曲線Cに沿って線積分可能という。
このとき、Wのことを、$\vec{F}(\vec x)$の曲線Cに沿った線積分といい、
$W=\int_{C}\vec{F}(\vec x)\cdot{d \vec x}$
と記す。
曲線に沿った仕事の定義
力$\vec{F}(\vec x)$が、向きつき曲線Cに沿って線積分可能であるとき、
$W=\lim_{n\to \infty}W({\Delta}^n, \{{\xi}^{n}_i\}_{i=1}^{n})=\int_{C}\vec{F}(\vec x)\cdot{d \vec x}$
を、力$\vec{F}(\vec x)$によって質点をCに沿って動かすときの、
力の行う行う仕事と定義する。
どのような条件があると線積分が可能になるか、とか、
この計算をこれ以上具体的に進めるには、
空間中の向きのついた曲線を数式で表現しなければならない。
連続な力の場のなす仕事
命題;連続な力の場のなす仕事
質点が連続な力の場から力$\vec{F}(\vec x)$を受け、
点$P$から点$Q$ まで曲線Cに沿って移動したとする。
この軌跡(曲線Cに、点$P$から点$Q$へむけた向きをいれたもの)が、
実数のある閉区間$I=[a,b]$上で定義された、
滑らかなベクトル値関数$\vec x=\vec{x}(p),(a\leq p \leq b)$で表せるならば、
力のなす仕事$W=\int_{C}\vec{F}(\vec x)\cdot{d \vec x}$は、
$W=\int_{a}^{b}\vec{F}(\vec x(p))\cdot \frac{d \vec x(p)}{dp}dp$
(注)滑らかな関数とは、$I=[a,b]$上で連続で、
開区間$I^{\circ}=(a,b)$で微分可能で導関数が連続なもの。
我々が経験するすべての曲線は、
曲線を表示するための、パラメータ区間上のベクトル値関数であらわせる。
この関数が滑らかというのが、この命題の課す制約である。
証明;
曲線Cにそった、力の線積分が可能であり、Wとなることを示す。
曲線の分割を得るため、パラメータの分割を行う。
パラメータ$a$から$b$までを、n個の小区間
$[p^{n}_{i-1},p^{n}_i](i=1,2,,,n)$に分割する。ここで$(p^{n}_0=a<p^{n}_{1}<p^{n}_{2},,,,<p^{n}_{n}=b)$
この分割を$\Delta^{n}:=\{[p^{n}_{i-1},p^{n}_i]\mid i=1,2,3,,,n\}$と書く。
n個の小区間の長さの最大値を$|\Delta^{n}|$と記す。$|\Delta^{n}|:=\max_{i}(p^{n}_i-p^{n}_{i-1})$
$\vec x^{n}_i:=\vec{x}(p^{n}_i)$(i=1,2,,,,,n)をCの分割の分点とすることで、
Cのn分割$C^{n}_i,(i=1,2,,,n)$が得られる。これを$\Delta'^n$と書く。
任意の$\eta^{n}_i \in [p^{n}_{i-1},p^{n}_i]$を選び
$\xi^{n}_i:=\vec{x}(\eta^{n}_i)$
を、$C^{n}_i$上の力の代表点とする。
$W({\Delta'}^n,\{{\xi}^{n}_i\}_{i=1}^{n})
=\sum_{i=1}^{n}W_{i}({\Delta'}^n,{\xi}^{n}_i) $
$=\sum_{i=1}^{n}\vec{F}({\xi}^{n}_i)\cdot ({\vec{x}^n}_i-{\vec{x}^n}_{i-1})$
$=\sum_{i=1}^{n}\vec{F}(\vec{x}(\eta^{n}_i))\cdot (\vec{x}(p^{n}_i)-\vec{x}(p^{n}_{i-1}))$
が、パラメータの分割を細かくしていくと、
分割$\Delta$ や $\eta^{n}_i$の選び方に無関係な定数に収束することを示せばよい。
$p^{n}_i- p^{n}_{i-1}$が小さいので、微分の定義から
$\frac{\vec{x}(p^{n}_i)- \vec{x}(p^{n}_{i-1})}{p^{n}_i)- p^{n}_{i-1}}
\approx \frac{d\vec{x}}{dp} (p^{n}_{i-1})$
そこで、
$\vec{x}(p^{n}_i)- \vec{x}(p^{n}_{i-1})$
$\approx
\frac{d\vec{x}}{dp} (p^{n}_{i-1})(p^{n}_i)- p^{n}_{i-1})$
故に、
$W^{n}_i \approx \vec{F}(p^{n}_{i-1})\cdot \frac{d\vec{x}}{dp} (p^{n}_{i-1})(p^{n}_i)- p^{n}_{i-1})$
$=(\vec{F}\cdot\frac{d\vec{x}}{dp})(p^{n}_{i-1}) (p^{n}_i)- p^{n}_{i-1})$
力がパラメータ区間$[a,b]$の間に行う仕事$W^n$は、
$W^n=\sum_{i=1}^{n}W^{n}_i $
$\approx
\sum_{i=1}^{n}(\vec{F}\cdot \frac{d\vec{x}}{dp})((p^{n}_{i-1}) (p^{n}_i)- p^{n}_{i-1})$
この式は、nが大きくなるほど、等式に近くなる。
最後の項$\sum_{i=1}^{n}(\vec{F}\cdot\frac{d\vec{x}}{dp})((p^{n}_{i-1}) (p^{n}_i)- p^{n}_{i-1})$は、
$[a,b]$上で定義された連続な実数値関数
$f(p):=(\vec{F}\cdot\frac{d\vec{x}}{dp})(p)=\vec{F}(p)\cdot\frac{d\vec{x}}{dp}(p)$
の、パラメータ区間の分割$\Delta^{n}:=\{[p^{n}_{i-1},p^{n}_i]\mid i=1,2,3,,,n\}$に対応する
リーマン和である。
そこで、nを無限に大きくしていくと、最後の式は
$W:=\lim_{n\to \infty}W^n=\int_{a}^{b}f(p)dp
=\int_{a}^{b}(\vec{F}\cdot\frac{d\vec{x}}{dp})(p)$
$=\int_{a}^{b}\vec{F}(p)\cdot \frac{d\vec{x}}{dp}(p)dp$
に収束する(8章の8.3 積分に証明あり)。
(注)この証明は、
「この式は、nが大きくなるほど、等式に近くなる」
ことの証明がないので、不正確である。
きちんとした証明は、8章物理数学の8.3積分で与える。
仕事の単位
仕事の定義$W=\|\vec F\|\|\vec s\| \cos\theta$から、仕事の単位は、力の大きさ$\|\vec F\|$の単位と長さ$\|\vec s\|$の単位を掛けたものになる($ \cos\theta$ は無単位なので )。
MKSA単位系では、力の大きさの単位は$N$(ニュートン)、長さの単位は$m$(メートル)なので、仕事の単位は$Nm$ となる。
これを$J$(ジュール)と呼ぶ。$J=Nm$である。