物理/この章の付録
提供: Internet Web School
目次 |
「7.6 この章の付録」
問の解答
問
UNIQ386cc4f10a9e570-MathJax-529-QINU が存在し、2より大きく3以下であることを証明する。
(1)準備; 2項定理を用いた展開
UNIQ386cc4f10a9e570-MathJax-530-QINU とおく。
すると、
UNIQ386cc4f10a9e570-MathJax-531-QINUである。
以下に、数列 UNIQ386cc4f10a9e570-MathJax-532-QINU が単調増大で、有界(2より大、3より小)である事を示す。
するとテキストの定理により、この数列は2より大きく、3以下のある実数に収束することが分かる。
nが3以上の自然数の時は、UNIQ386cc4f10a9e570-MathJax-533-QINUを2項定理を用いて展開すると
UNIQ386cc4f10a9e570-MathJax-534-QINU
ここで UNIQ386cc4f10a9e570-MathJax-535-QINU は、n個のものからm個取り出す取り出し方の総数で、
mが1以上でn 以下の自然数の時は
UNIQ386cc4f10a9e570-MathJax-536-QINU
ここで、m が1以上の自然数の時は UNIQ386cc4f10a9e570-MathJax-537-QINU
mが零の時は UNIQ386cc4f10a9e570-MathJax-538-QINU と定義。
すると、
UNIQ386cc4f10a9e570-MathJax-539-QINU
UNIQ386cc4f10a9e570-MathJax-540-QINUのとき、UNIQ386cc4f10a9e570-MathJax-541-QINU
式(1)に式(2)を代入し,式(3)、(4)を利用して計算すると
UNIQ386cc4f10a9e570-MathJax-542-QINU
UNIQ386cc4f10a9e570-MathJax-543-QINU
ここで、n より小さい全ての自然数 i に対して
UNIQ386cc4f10a9e570-MathJax-544-QINU なので、
UNIQ386cc4f10a9e570-MathJax-545-QINU
(2)すべての2以上の自然数 n に関して、
UNIQ386cc4f10a9e570-MathJax-546-QINU
であることを示す。
式(6)から
UNIQ386cc4f10a9e570-MathJax-547-QINU,
UNIQ386cc4f10a9e570-MathJax-548-QINU
右辺の m は2以上の自然数なので、
UNIQ386cc4f10a9e570-MathJax-549-QINU
である。故に、
UNIQ386cc4f10a9e570-MathJax-550-QINU
(3)数列 UNIQ386cc4f10a9e570-MathJax-551-QINU は単調増加
UNIQ386cc4f10a9e570-MathJax-552-QINU の時、常に UNIQ386cc4f10a9e570-MathJax-553-QINU を示せばよい。
式(5)を利用すると(注参照)、
UNIQ386cc4f10a9e570-MathJax-554-QINU
すると、
UNIQ386cc4f10a9e570-MathJax-555-QINU
UNIQ386cc4f10a9e570-MathJax-556-QINU 右辺の第一項の和を2つに分けると、
UNIQ386cc4f10a9e570-MathJax-557-QINU
UNIQ386cc4f10a9e570-MathJax-558-QINU
UNIQ386cc4f10a9e570-MathJax-559-QINU
UNIQ386cc4f10a9e570-MathJax-560-QINU
上の式で、全てのUNIQ386cc4f10a9e570-MathJax-561-QINUに対して,UNIQ386cc4f10a9e570-MathJax-562-QINUとUNIQ386cc4f10a9e570-MathJax-563-QINU なので、
UNIQ386cc4f10a9e570-MathJax-564-QINU
(注)式(3)のnに n+1 を代入すればよい。
ネイピア数 e について
定義;UNIQ386cc4f10a9e570-MathJax-565-QINU をネイピア数と呼ぶ。
命題1
(1)UNIQ386cc4f10a9e570-MathJax-566-QINU
(2)UNIQ386cc4f10a9e570-MathJax-567-QINU
三角関数の微分
準備
次の命題が、三角関数の微分を求めるうえで中心的役割を果たす。
命題2
UNIQ386cc4f10a9e570-MathJax-568-QINU
証明
まず、UNIQ386cc4f10a9e570-MathJax-569-QINU を正に保ちながら零に近づける場合を考える。
すると、UNIQ386cc4f10a9e570-MathJax-570-QINU と考えて良い。
点Oを中心にし、半径1の円を考え、円周上に一点Aをさだめる。
図のように、円周上の点Bを、線分OBが直線OAとなす角がx(ラジアン)となるようにとる。
図からUNIQ386cc4f10a9e570-MathJax-571-QINU
UNIQ386cc4f10a9e570-MathJax-572-QINU ここで、点PはAを通り線分OAと垂直な直線と半直線OBの交点。
すると、
UNIQ386cc4f10a9e570-MathJax-573-QINU
ここで、UNIQ386cc4f10a9e570-MathJax-574-QINUなので、
UNIQ386cc4f10a9e570-MathJax-575-QINU各項を2倍すると、
UNIQ386cc4f10a9e570-MathJax-576-QINU
UNIQ386cc4f10a9e570-MathJax-577-QINUここで UNIQ386cc4f10a9e570-MathJax-578-QINU なので、これで上式の各項を割ると、
UNIQ386cc4f10a9e570-MathJax-579-QINU
UNIQ386cc4f10a9e570-MathJax-580-QINU
故に、極限の性質から
UNIQ386cc4f10a9e570-MathJax-581-QINU
これより、UNIQ386cc4f10a9e570-MathJax-582-QINU が得られる。
定理1 三角関数の微分
(1)UNIQ386cc4f10a9e570-MathJax-583-QINU
(2)UNIQ386cc4f10a9e570-MathJax-584-QINU
証明
(1); UNIQ386cc4f10a9e570-MathJax-585-QINU
ここで、
UNIQ386cc4f10a9e570-MathJax-586-QINU
サイン関数の加法定理を適用すると
UNIQ386cc4f10a9e570-MathJax-587-QINU
故に、
UNIQ386cc4f10a9e570-MathJax-588-QINU
UNIQ386cc4f10a9e570-MathJax-589-QINU
UNIQ386cc4f10a9e570-MathJax-590-QINU ここで、
UNIQ386cc4f10a9e570-MathJax-591-QINU
UNIQ386cc4f10a9e570-MathJax-592-QINU
UNIQ386cc4f10a9e570-MathJax-593-QINUなので、
UNIQ386cc4f10a9e570-MathJax-594-QINU
指数関数と対数関数
正の実数の累乗の指数の拡張
実数の累乗(自然数乗)
UNIQ386cc4f10a9e570-MathJax-595-QINU を任意の実数、UNIQ386cc4f10a9e570-MathJax-596-QINU を2以上の自然数とする。
UNIQ386cc4f10a9e570-MathJax-597-QINU
を総称して、a の累乗と呼ぶ。
UNIQ386cc4f10a9e570-MathJax-598-QINU をUNIQ386cc4f10a9e570-MathJax-599-QINU の n 乗 、UNIQ386cc4f10a9e570-MathJax-600-QINU をその指数と呼ぶ。
実数の自然数乗の3つの計算規則
累乗が次のような計算規則を満たすことは、容易に証明できる。
命題3
UNIQ386cc4f10a9e570-MathJax-601-QINU を任意の実数、UNIQ386cc4f10a9e570-MathJax-602-QINU を任意の自然数とすると、
(1) UNIQ386cc4f10a9e570-MathJax-603-QINU
(2) UNIQ386cc4f10a9e570-MathJax-604-QINU
(3) UNIQ386cc4f10a9e570-MathJax-605-QINU
証明は、累乗の定義と積の交換法則から容易にできるので省略する。
指数関数とn次関数
UNIQ386cc4f10a9e570-MathJax-606-QINU を正の実数とするとき、累乗UNIQ386cc4f10a9e570-MathJax-607-QINU の
UNIQ386cc4f10a9e570-MathJax-608-QINU を独立変数とするか、UNIQ386cc4f10a9e570-MathJax-609-QINU を独立変数にするかで、
次の2種の関数が定まる。
定義
UNIQ386cc4f10a9e570-MathJax-610-QINU を正の実数, UNIQ386cc4f10a9e570-MathJax-611-QINUを自然数とするとき、次の2つの関数を考える。
1)UNIQ386cc4f10a9e570-MathJax-612-QINU
これは、指数を変数とする関数なので、指数関数という。
2)UNIQ386cc4f10a9e570-MathJax-613-QINU
これは、UNIQ386cc4f10a9e570-MathJax-614-QINU次の単項関数である。
命題 指数関数の性質
指数関数UNIQ386cc4f10a9e570-MathJax-615-QINU は次の性質を持つ。
1)UNIQ386cc4f10a9e570-MathJax-616-QINUのとき、UNIQ386cc4f10a9e570-MathJax-617-QINUからUNIQ386cc4f10a9e570-MathJax-618-QINUへの狭義単調減少の連続関数で、UNIQ386cc4f10a9e570-MathJax-619-QINU
2)UNIQ386cc4f10a9e570-MathJax-620-QINUのとき、UNIQ386cc4f10a9e570-MathJax-621-QINUからUNIQ386cc4f10a9e570-MathJax-622-QINUへの狭義単調増加の連続関数
で、
UNIQ386cc4f10a9e570-MathJax-623-QINU
連続性以外は、明らかなので証明は省略する。
自然数全体の集合UNIQ386cc4f10a9e570-MathJax-624-QINUは離散集合なので、
そのうえで定義された任意の関数は連続となる。
「8.2 解析入門(1)実数の性質、連続関数、微分 UNIQ386cc4f10a9e570-MathJax-625-QINU 「1.3 関数とその連続性」の「1.3.2 関数の極限と連続性」を参照のこと。
命題 UNIQ386cc4f10a9e570-MathJax-626-QINU次の単項関数の性質
UNIQ386cc4f10a9e570-MathJax-627-QINU とする。
UNIQ386cc4f10a9e570-MathJax-628-QINU次の単項関数UNIQ386cc4f10a9e570-MathJax-629-QINU は
UNIQ386cc4f10a9e570-MathJax-630-QINUからUNIQ386cc4f10a9e570-MathJax-631-QINUへの狭義単調増加の連続関数で、
UNIQ386cc4f10a9e570-MathJax-632-QINU
UNIQ386cc4f10a9e570-MathJax-633-QINU
である。
証明
UNIQ386cc4f10a9e570-MathJax-634-QINU上では狭義単調増加であることは容易に示せる。
連続性については、UNIQ386cc4f10a9e570-MathJax-635-QINU であることを示せばよい。
例えば、2項定理でUNIQ386cc4f10a9e570-MathJax-636-QINU を展開して極限をとればよい。
この節の目的
この節の目的は、累乗にかんする計算規則を満たすようにしながら、
累乗の指数を実数まで拡張することである。
しかし UNIQ386cc4f10a9e570-MathJax-637-QINU が負数だと、指数を有理数に拡張するとき不都合が起きてしまう。
例えば
UNIQ386cc4f10a9e570-MathJax-638-QINU の時, UNIQ386cc4f10a9e570-MathJax-639-QINU は実数でなく虚数となり、
実数値関数の枠組みに収まらなくなる。
そこで、このような不都合が起こらないように 今後はUNIQ386cc4f10a9e570-MathJax-640-QINU を正の実数に限定し、
次の計算規則を満たすようにしながら、指数を自然数から整数、整数から有理数、有理数から実数へと順に拡張していく。
累乗に関する計算規則
UNIQ386cc4f10a9e570-MathJax-641-QINU を任意の正の実数、UNIQ386cc4f10a9e570-MathJax-642-QINUを指数とすると、
(1) UNIQ386cc4f10a9e570-MathJax-643-QINU
(2) UNIQ386cc4f10a9e570-MathJax-644-QINU
(3) UNIQ386cc4f10a9e570-MathJax-645-QINU
計算規則(3)を守ろうとすると、UNIQ386cc4f10a9e570-MathJax-646-QINU と定めなければならないことが分かる。
何故ならば UNIQ386cc4f10a9e570-MathJax-647-QINUの時、UNIQ386cc4f10a9e570-MathJax-648-QINU となり、 UNIQ386cc4f10a9e570-MathJax-649-QINU であるから。
そこで 今後は常に UNIQ386cc4f10a9e570-MathJax-650-QINU と定め、 UNIQ386cc4f10a9e570-MathJax-651-QINU の場合だけを考察する。
本節のもう一つの目的は、指数の拡張に伴い累乗に伴う2つの関数
UNIQ386cc4f10a9e570-MathJax-652-QINU とUNIQ386cc4f10a9e570-MathJax-653-QINU の性質が、どのようになるか考察する事である。
指数の整数への拡張
任意の正の実数UNIQ386cc4f10a9e570-MathJax-654-QINU を考える。
UNIQ386cc4f10a9e570-MathJax-655-QINUの累乗の指数を、累乗に関する3つの規則が成り立つようにしながら、整数に拡張しよう。
まず、規則(1)を守ろうとすれば
UNIQ386cc4f10a9e570-MathJax-656-QINU
と定義しなければならないことが分かる。
何故ならば、UNIQ386cc4f10a9e570-MathJax-657-QINU の時、
UNIQ386cc4f10a9e570-MathJax-658-QINU
となり、 UNIQ386cc4f10a9e570-MathJax-659-QINU だから両辺を UNIQ386cc4f10a9e570-MathJax-660-QINU で割ればよい。
次に任意の自然数 n に対して、
UNIQ386cc4f10a9e570-MathJax-661-QINU を累乗に関する規則(1)を満たすように定義しよう。
UNIQ386cc4f10a9e570-MathJax-662-QINU
両辺を UNIQ386cc4f10a9e570-MathJax-663-QINU で割れば
UNIQ386cc4f10a9e570-MathJax-664-QINU
命題
式(4),(5)に従って指数を整数に拡大すると、
3つの累乗の規則はすべて成立する。
証明
指数が負のときは式(5)を用いて、指数が自然数の式に書き直し、
指数が自然数のときに成り立つことが分かっている3つの計算規則を使って式の変形をすれば良い。
計算規則の(1)の証明だけを示そう。
(1)UNIQ386cc4f10a9e570-MathJax-665-QINU を任意の整数とすると、
UNIQ386cc4f10a9e570-MathJax-666-QINU であることを示す。
(ケース1)指数の一方が正の整数(自然数)で、他方が負の整数の時
UNIQ386cc4f10a9e570-MathJax-667-QINU を自然数として、
UNIQ386cc4f10a9e570-MathJax-668-QINU を示せばよい。
式(5)から
UNIQ386cc4f10a9e570-MathJax-669-QINU
UNIQ386cc4f10a9e570-MathJax-670-QINU 、UNIQ386cc4f10a9e570-MathJax-671-QINU 、UNIQ386cc4f10a9e570-MathJax-672-QINU という3つの場合に分けて証明する。
1)UNIQ386cc4f10a9e570-MathJax-673-QINU の時
割り算を実行するとUNIQ386cc4f10a9e570-MathJax-674-QINU
この式と、式(6)から、UNIQ386cc4f10a9e570-MathJax-675-QINU
2) UNIQ386cc4f10a9e570-MathJax-676-QINU の時
UNIQ386cc4f10a9e570-MathJax-677-QINU
この式と、式(6)から、UNIQ386cc4f10a9e570-MathJax-678-QINU
3) UNIQ386cc4f10a9e570-MathJax-679-QINU の時
割り算を実行すると、
UNIQ386cc4f10a9e570-MathJax-680-QINU
UNIQ386cc4f10a9e570-MathJax-681-QINU
(ケース2)両方の指数が負の整数の時
UNIQ386cc4f10a9e570-MathJax-682-QINU を示せばよい。
UNIQ386cc4f10a9e570-MathJax-683-QINU
指数の有理数への拡張
これ以降、有理数全体のなす集合をUNIQ386cc4f10a9e570-MathJax-684-QINUとかく。
UNIQ386cc4f10a9e570-MathJax-685-QINU を任意の正の実数、 UNIQ386cc4f10a9e570-MathJax-686-QINU を任意の有理数のとき、
UNIQ386cc4f10a9e570-MathJax-687-QINU の有理数乗 UNIQ386cc4f10a9e570-MathJax-688-QINU を、計算規則を満たすように定義しよう。
指数n を任意の自然数(正の整数)、 m を任意の整数と仮定してよい。
UNIQ386cc4f10a9e570-MathJax-689-QINU(注)nが負の時はUNIQ386cc4f10a9e570-MathJax-690-QINU なので、
UNIQ386cc4f10a9e570-MathJax-691-QINUを改めてUNIQ386cc4f10a9e570-MathJax-692-QINU と置けば良い。UNIQ386cc4f10a9e570-MathJax-693-QINU
累乗規則(2)を満たすように定義するには、
UNIQ386cc4f10a9e570-MathJax-694-QINU
でなければならない。
これは、UNIQ386cc4f10a9e570-MathJax-695-QINU が UNIQ386cc4f10a9e570-MathJax-696-QINU のn乗根であることを示す。
しかしnが偶数のときは、UNIQ386cc4f10a9e570-MathJax-697-QINU もUNIQ386cc4f10a9e570-MathJax-698-QINU のn乗根となるので、
正のn乗根 のほうを、UNIQ386cc4f10a9e570-MathJax-699-QINU とかく。
定義 正の実数の有理数乗
UNIQ386cc4f10a9e570-MathJax-700-QINUを正の実数とする。
UNIQ386cc4f10a9e570-MathJax-701-QINU とは、
UNIQ386cc4f10a9e570-MathJax-702-QINU の正のn乗根である。
すなわち、
UNIQ386cc4f10a9e570-MathJax-703-QINUを満たす正の実数である。
最初に、この定義できちんと正の実数が一つだけ決まることを証明しよう。
UNIQ386cc4f10a9e570-MathJax-704-QINUのときは、n乗すると1になる正数は1だけなので
UNIQ386cc4f10a9e570-MathJax-705-QINU
であることが分かるので、UNIQ386cc4f10a9e570-MathJax-706-QINU の場合を考える。
命題3
UNIQ386cc4f10a9e570-MathJax-707-QINU を任意の正の実数、UNIQ386cc4f10a9e570-MathJax-708-QINU を任意の整数,UNIQ386cc4f10a9e570-MathJax-709-QINUを任意の自然数とする。
すると、n 乗すると UNIQ386cc4f10a9e570-MathJax-710-QINU になる正の実数 UNIQ386cc4f10a9e570-MathJax-711-QINU (i.e. UNIQ386cc4f10a9e570-MathJax-712-QINU)が存在し、ただ一つに限る。
証明
(1) 存在性
UNIQ386cc4f10a9e570-MathJax-713-QINU という、零と正の実数の上で定義された、関数を考える。
この関数はxが増加するにつれて、連続的に、零から正の無限大に狭義に単調に増加(注参照)していく。
そこで、UNIQ386cc4f10a9e570-MathJax-714-QINU という集合を考える。
この集合は、上に有界な区間になり、実数の連続性から上限(sup)UNIQ386cc4f10a9e570-MathJax-715-QINUを持つ。
この時、UNIQ386cc4f10a9e570-MathJax-716-QINU であることを示そう。
UNIQ386cc4f10a9e570-MathJax-717-QINU が集合UNIQ386cc4f10a9e570-MathJax-718-QINUの上限なので、任意の自然数nに対して、
UNIQ386cc4f10a9e570-MathJax-719-QINU
を満たす UNIQ386cc4f10a9e570-MathJax-720-QINU が存在する。
明らかに
UNIQ386cc4f10a9e570-MathJax-721-QINU
すると、関数 UNIQ386cc4f10a9e570-MathJax-722-QINU は連続なので、
UNIQ386cc4f10a9e570-MathJax-723-QINU
ところがUNIQ386cc4f10a9e570-MathJax-724-QINUなので、
UNIQ386cc4f10a9e570-MathJax-725-QINU
式(a)、(b) から、UNIQ386cc4f10a9e570-MathJax-726-QINU がえられるので、
UNIQ386cc4f10a9e570-MathJax-727-QINU
が示せた。(従って、Bは閉区間 [o,b] である。)
UNIQ386cc4f10a9e570-MathJax-728-QINU であることを背理法を使って示そう。
もし、UNIQ386cc4f10a9e570-MathJax-729-QINU だとすると、関数 UNIQ386cc4f10a9e570-MathJax-730-QINU は連続なので
充分小さな正の実数UNIQ386cc4f10a9e570-MathJax-731-QINU をとると、UNIQ386cc4f10a9e570-MathJax-732-QINU を満たす。
すると UNIQ386cc4f10a9e570-MathJax-733-QINU となり、
UNIQ386cc4f10a9e570-MathJax-734-QINUが B の上限であることに矛盾してしまう。
故に、背理法により、UNIQ386cc4f10a9e570-MathJax-735-QINU が証明できた。
(2)一意性
関数 UNIQ386cc4f10a9e570-MathJax-736-QINU は狭義の単調増加関数なのでb以外の数b'(UNIQ386cc4f10a9e570-MathJax-737-QINU)では、
UNIQ386cc4f10a9e570-MathJax-738-QINU
(証明終り) UNIQ386cc4f10a9e570-MathJax-739-QINU
(注) 関数fが狭義単調増加とは、UNIQ386cc4f10a9e570-MathJax-740-QINU を満たすこと。
命題4
任意の正の実数 UNIQ386cc4f10a9e570-MathJax-741-QINU にたいして、その有理数乗を上記のように定義すると
3つの累乗規則 (1)~(3) が成り立つ。
証明;
1) 累乗規則(1)が成り立つことを示す。
2個の有理数の指数を 自然数UNIQ386cc4f10a9e570-MathJax-742-QINUと整数UNIQ386cc4f10a9e570-MathJax-743-QINU を用いて、
UNIQ386cc4f10a9e570-MathJax-744-QINUと表現する。
すると、累乗規則(1)は、次のように表される。
UNIQ386cc4f10a9e570-MathJax-745-QINU
この左辺を UNIQ386cc4f10a9e570-MathJax-746-QINU,
右辺を UNIQ386cc4f10a9e570-MathJax-747-QINU とおく。
UNIQ386cc4f10a9e570-MathJax-748-QINU
であることを示せば、UNIQ386cc4f10a9e570-MathJax-749-QINU が得られ,
累乗規則(1)が成立することが分かる。
まず左辺を考える。
UNIQ386cc4f10a9e570-MathJax-750-QINU
指数が自然数の累乗規則(3)から
UNIQ386cc4f10a9e570-MathJax-751-QINU
指数が自然数の累乗規則(2)から
UNIQ386cc4f10a9e570-MathJax-752-QINU
実数の有理数乗の定義から、
UNIQ386cc4f10a9e570-MathJax-753-QINU
指数が整数の累乗規則(2)から
UNIQ386cc4f10a9e570-MathJax-754-QINU
指数が整数の累乗規則(1)から
UNIQ386cc4f10a9e570-MathJax-755-QINU
故に、UNIQ386cc4f10a9e570-MathJax-756-QINU
次に、右辺を考える。
UNIQ386cc4f10a9e570-MathJax-757-QINU
UNIQ386cc4f10a9e570-MathJax-758-QINU
実数の有理数乗の定義から、
UNIQ386cc4f10a9e570-MathJax-759-QINU
これで、式(a)が示され、累乗規則(1)が成り立つことが証明できた。
2)累乗規則(2)と累乗規則(3)が成り立つことは読者がしてください。
証明終わり。
指数が有理数の場合,命題2は次のように拡張出来る。
命題5
UNIQ386cc4f10a9e570-MathJax-760-QINUの上で定義される関数
UNIQ386cc4f10a9e570-MathJax-761-QINUを考える。
1)UNIQ386cc4f10a9e570-MathJax-762-QINU を1より大きい正の実数とすると、
UNIQ386cc4f10a9e570-MathJax-763-QINUは単調増大で
UNIQ386cc4f10a9e570-MathJax-764-QINU
2)UNIQ386cc4f10a9e570-MathJax-765-QINU が1より小さい正の実数のとき、
UNIQ386cc4f10a9e570-MathJax-766-QINUは単調減少し、
UNIQ386cc4f10a9e570-MathJax-767-QINU
3)UNIQ386cc4f10a9e570-MathJax-768-QINU のとき、UNIQ386cc4f10a9e570-MathJax-769-QINU
証明
1)のみ証明する。2)の場合も同様に証明できる。
① UNIQ386cc4f10a9e570-MathJax-770-QINU とすると、
UNIQ386cc4f10a9e570-MathJax-771-QINU を示そう。
UNIQ386cc4f10a9e570-MathJax-772-QINU
を示せばよい。
正数の有理数乗の計算規則から、
UNIQ386cc4f10a9e570-MathJax-773-QINU
UNIQ386cc4f10a9e570-MathJax-774-QINU
故に、
UNIQ386cc4f10a9e570-MathJax-775-QINU
UNIQ386cc4f10a9e570-MathJax-776-QINU から、
UNIQ386cc4f10a9e570-MathJax-777-QINUなので、UNIQ386cc4f10a9e570-MathJax-778-QINUであり
UNIQ386cc4f10a9e570-MathJax-779-QINU
故に、 UNIQ386cc4f10a9e570-MathJax-780-QINU
自然数乗すると1より大きくなる正の実数は1より大きい実数しかないので、
UNIQ386cc4f10a9e570-MathJax-781-QINU が得られた。
② UNIQ386cc4f10a9e570-MathJax-782-QINUを示そう。
関数 UNIQ386cc4f10a9e570-MathJax-783-QINU は単調増加(①で証明)なので、
UNIQ386cc4f10a9e570-MathJax-784-QINU
を示せばよいが、これは自明である。
③ UNIQ386cc4f10a9e570-MathJax-785-QINU
も、同様にして示せる。
証明終わり UNIQ386cc4f10a9e570-MathJax-786-QINU
以上の結果をまとめて、次の定理を得る。
UNIQ386cc4f10a9e570-MathJax-787-QINU
UNIQ386cc4f10a9e570-MathJax-788-QINU の正の実数とする。
(1)UNIQ386cc4f10a9e570-MathJax-789-QINU の有理数乗 UNIQ386cc4f10a9e570-MathJax-790-QINU をUNIQ386cc4f10a9e570-MathJax-791-QINUの正のUNIQ386cc4f10a9e570-MathJax-792-QINU乗根で定義すると、
累乗に関する計算規則
UNIQ386cc4f10a9e570-MathJax-793-QINU を任意の正の実数、UNIQ386cc4f10a9e570-MathJax-794-QINUを指数とすると、
UNIQ386cc4f10a9e570-MathJax-795-QINU 1) UNIQ386cc4f10a9e570-MathJax-796-QINU
UNIQ386cc4f10a9e570-MathJax-797-QINU 2) UNIQ386cc4f10a9e570-MathJax-798-QINU
UNIQ386cc4f10a9e570-MathJax-799-QINU 3) UNIQ386cc4f10a9e570-MathJax-800-QINU
を満たす。
(2)UNIQ386cc4f10a9e570-MathJax-801-QINUの上で定義される関数
UNIQ386cc4f10a9e570-MathJax-802-QINUを考えると、
UNIQ386cc4f10a9e570-MathJax-803-QINU1)UNIQ386cc4f10a9e570-MathJax-804-QINU のとき、 UNIQ386cc4f10a9e570-MathJax-805-QINUは狭義の単調増大(従って一対一)で、
UNIQ386cc4f10a9e570-MathJax-806-QINU UNIQ386cc4f10a9e570-MathJax-807-QINU
UNIQ386cc4f10a9e570-MathJax-808-QINU 2)UNIQ386cc4f10a9e570-MathJax-809-QINU のとき、 UNIQ386cc4f10a9e570-MathJax-810-QINUは狭義の単調減少(従って一対一)で、
UNIQ386cc4f10a9e570-MathJax-811-QINU
UNIQ386cc4f10a9e570-MathJax-812-QINU 3)UNIQ386cc4f10a9e570-MathJax-813-QINU のとき、UNIQ386cc4f10a9e570-MathJax-814-QINU
(3)関数 UNIQ386cc4f10a9e570-MathJax-815-QINUは連続関数である。
すなわち、
UNIQ386cc4f10a9e570-MathJax-816-QINU
ならば、
UNIQ386cc4f10a9e570-MathJax-817-QINU
証明
(1)、(2)はすでに証明したことなので、(3)だけを証明する。
UNIQ386cc4f10a9e570-MathJax-818-QINU なので、
UNIQ386cc4f10a9e570-MathJax-819-QINU
を、示せばよい。
UNIQ386cc4f10a9e570-MathJax-820-QINU とおくと、
UNIQ386cc4f10a9e570-MathJax-821-QINU
を示せばよい。
このために、次の補題をまず証明する。
補題
UNIQ386cc4f10a9e570-MathJax-822-QINU
UNIQ386cc4f10a9e570-MathJax-823-QINU
補題の証明
1) 式(b)を背理法で証明する。
もし式(b)が成立しないとする。
すると或る小さな正数UNIQ386cc4f10a9e570-MathJax-824-QINU が存在し、
どのような自然数 UNIQ386cc4f10a9e570-MathJax-825-QINU をとっても、ある自然数UNIQ386cc4f10a9e570-MathJax-826-QINU が存在して
UNIQ386cc4f10a9e570-MathJax-827-QINU
となる。(注参照)
すると、自然数の部分列 UNIQ386cc4f10a9e570-MathJax-828-QINU が存在して、
UNIQ386cc4f10a9e570-MathJax-829-QINU
となる。
① UNIQ386cc4f10a9e570-MathJax-830-QINU の場合
UNIQ386cc4f10a9e570-MathJax-831-QINUなので、
UNIQ386cc4f10a9e570-MathJax-832-QINU
すなわち、
UNIQ386cc4f10a9e570-MathJax-833-QINU
両辺をUNIQ386cc4f10a9e570-MathJax-834-QINU乗して
UNIQ386cc4f10a9e570-MathJax-835-QINU
2項定理から
UNIQ386cc4f10a9e570-MathJax-836-QINU
であることがわかるので、
UNIQ386cc4f10a9e570-MathJax-837-QINU
UNIQ386cc4f10a9e570-MathJax-838-QINU なので、
式(e)から、UNIQ386cc4f10a9e570-MathJax-839-QINU となり、矛盾が生じてしまう。
② UNIQ386cc4f10a9e570-MathJax-840-QINU の場合も同様にして、矛盾が生じることが示せる。
③ 故に、式(b)が成立しないと仮定すると矛盾が生じるので、
背理法により、式(b)が成立することが、証明できた。
2)式(c)の証明も同様にしてできるので省略する。UNIQ386cc4f10a9e570-MathJax-841-QINU
任意の正数UNIQ386cc4f10a9e570-MathJax-842-QINU に対して、ある番号UNIQ386cc4f10a9e570-MathJax-843-QINUが定まって、
UNIQ386cc4f10a9e570-MathJax-844-QINUというすべての自然数UNIQ386cc4f10a9e570-MathJax-845-QINUに対して、
UNIQ386cc4f10a9e570-MathJax-846-QINU
を示せば、
UNIQ386cc4f10a9e570-MathJax-847-QINU
が示せて、証明が終了する。
補題により、UNIQ386cc4f10a9e570-MathJax-848-QINU に対して、ある番号UNIQ386cc4f10a9e570-MathJax-849-QINUをさだめ,
UNIQ386cc4f10a9e570-MathJax-850-QINUならば、
UNIQ386cc4f10a9e570-MathJax-851-QINU
UNIQ386cc4f10a9e570-MathJax-852-QINU
が成立するようにできる。
UNIQ386cc4f10a9e570-MathJax-853-QINU
なので、
自然数UNIQ386cc4f10a9e570-MathJax-854-QINUに対して、
ある番号UNIQ386cc4f10a9e570-MathJax-855-QINU が存在して、
UNIQ386cc4f10a9e570-MathJax-856-QINU以上のどんな自然数UNIQ386cc4f10a9e570-MathJax-857-QINUに対しても、
UNIQ386cc4f10a9e570-MathJax-858-QINU
すると指数関数UNIQ386cc4f10a9e570-MathJax-859-QINU の単調性から、
UNIQ386cc4f10a9e570-MathJax-860-QINU は、UNIQ386cc4f10a9e570-MathJax-861-QINUとUNIQ386cc4f10a9e570-MathJax-862-QINUの間の数となり、
UNIQ386cc4f10a9e570-MathJax-863-QINU
が示せた。
定理の証明終わり。 UNIQ386cc4f10a9e570-MathJax-864-QINU
指数の実数への拡張
UNIQ386cc4f10a9e570-MathJax-865-QINU を、正の実数とする。
任意の実数 UNIQ386cc4f10a9e570-MathJax-866-QINU に対して 指数 UNIQ386cc4f10a9e570-MathJax-867-QINU を定義しよう。
UNIQ386cc4f10a9e570-MathJax-868-QINU
1)UNIQ386cc4f10a9e570-MathJax-869-QINU を UNIQ386cc4f10a9e570-MathJax-870-QINU に収束する有理数の単調増加数列とするとき、
UNIQ386cc4f10a9e570-MathJax-871-QINU
2)UNIQ386cc4f10a9e570-MathJax-872-QINU を UNIQ386cc4f10a9e570-MathJax-873-QINU に収束する有理数の単調減少数列とするとき、
UNIQ386cc4f10a9e570-MathJax-874-QINU
UNIQ386cc4f10a9e570-MathJax-875-QINU
1)定義の式(a)、(b) は収束する。
2)UNIQ386cc4f10a9e570-MathJax-876-QINU に収束する、別の,
UNIQ386cc4f10a9e570-MathJax-877-QINU 有理数の単調増加数列UNIQ386cc4f10a9e570-MathJax-878-QINUと単調減少数列UNIQ386cc4f10a9e570-MathJax-879-QINU をとっても、
UNIQ386cc4f10a9e570-MathJax-880-QINU UNIQ386cc4f10a9e570-MathJax-881-QINU
3)UNIQ386cc4f10a9e570-MathJax-882-QINU
証明
UNIQ386cc4f10a9e570-MathJax-883-QINU の場合は 1の有理数乗は常に1になるので命題は明らかである。
UNIQ386cc4f10a9e570-MathJax-884-QINU の場合を証明する。UNIQ386cc4f10a9e570-MathJax-885-QINU の場合も同じように証明できる。
1)UNIQ386cc4f10a9e570-MathJax-886-QINU上の関数 UNIQ386cc4f10a9e570-MathJax-887-QINU は単調増加(定理1)なので、
UNIQ386cc4f10a9e570-MathJax-888-QINU は上に有界な単調増加数列、
UNIQ386cc4f10a9e570-MathJax-889-QINUは下に有界な単調減少数列となる。
このため、「8.2 解析入門(1)」の
「1.2.3 実数列の極限」の定理1から、
これらは、ともに収束することが保証される。
2)UNIQ386cc4f10a9e570-MathJax-890-QINUを示そう。
UNIQ386cc4f10a9e570-MathJax-891-QINU
とおく。
すると、UNIQ386cc4f10a9e570-MathJax-892-QINU
定理1(有理数を累乗とする指数関数の連続性)から、
UNIQ386cc4f10a9e570-MathJax-893-QINU
UNIQ386cc4f10a9e570-MathJax-894-QINU
UNIQ386cc4f10a9e570-MathJax-895-QINU
故に、
UNIQ386cc4f10a9e570-MathJax-896-QINU
上式の分子も分母も収束するので
UNIQ386cc4f10a9e570-MathJax-897-QINU
3)2)の証明と殆ど同じようにして出来る。
UNIQ386cc4f10a9e570-MathJax-898-QINU を UNIQ386cc4f10a9e570-MathJax-899-QINU に収束する有理数の単調増加数列
UNIQ386cc4f10a9e570-MathJax-900-QINU を UNIQ386cc4f10a9e570-MathJax-901-QINU に収束する有理数の単調減少数列とする。
UNIQ386cc4f10a9e570-MathJax-902-QINU
とおく。
すると、UNIQ386cc4f10a9e570-MathJax-903-QINU
定理1(有理数を累乗とする指数関数の連続性)から、
UNIQ386cc4f10a9e570-MathJax-904-QINU
UNIQ386cc4f10a9e570-MathJax-905-QINU
UNIQ386cc4f10a9e570-MathJax-906-QINU
故に、
UNIQ386cc4f10a9e570-MathJax-907-QINU
上式の分子も分母も収束するので
UNIQ386cc4f10a9e570-MathJax-908-QINU
証明終わり。UNIQ386cc4f10a9e570-MathJax-909-QINU
UNIQ386cc4f10a9e570-MathJax-910-QINU
UNIQ386cc4f10a9e570-MathJax-911-QINU を任意の正の実数、UNIQ386cc4f10a9e570-MathJax-912-QINU を任意の実数とするとき、
UNIQ386cc4f10a9e570-MathJax-913-QINU の UNIQ386cc4f10a9e570-MathJax-914-QINU乗を、
UNIQ386cc4f10a9e570-MathJax-915-QINU
で定義する。
UNIQ386cc4f10a9e570-MathJax-916-QINU
1)任意の正の実数UNIQ386cc4f10a9e570-MathJax-917-QINU に対して、その実数乗を上述のように定義すると、
累乗の計算規則を満たす。
2)実数空間 UNIQ386cc4f10a9e570-MathJax-918-QINU で定義された指数関数
UNIQ386cc4f10a9e570-MathJax-919-QINU
は、UNIQ386cc4f10a9e570-MathJax-920-QINU ならば、一対一関数で
UNIQ386cc4f10a9e570-MathJax-921-QINU ならば単調増加、UNIQ386cc4f10a9e570-MathJax-922-QINU ならば単調減少である
3)UNIQ386cc4f10a9e570-MathJax-923-QINU ならば、指数関数UNIQ386cc4f10a9e570-MathJax-924-QINU は UNIQ386cc4f10a9e570-MathJax-925-QINUから無限開区間UNIQ386cc4f10a9e570-MathJax-926-QINUの上への、連続関数である。
証明
1)UNIQ386cc4f10a9e570-MathJax-927-QINU を任意の正の実数、UNIQ386cc4f10a9e570-MathJax-928-QINUを実数とすると、
UNIQ386cc4f10a9e570-MathJax-929-QINU を示せばよい。
皆同じように証明できるので、規則1だけを証明する。
実数 UNIQ386cc4f10a9e570-MathJax-930-QINU に収束する任意の有理数の単調増加列 UNIQ386cc4f10a9e570-MathJax-931-QINU と、
実数 UNIQ386cc4f10a9e570-MathJax-932-QINU に収束する任意の有理数の単調増加列 UNIQ386cc4f10a9e570-MathJax-933-QINU をとれば、
定理1から、有理数乗では規則1は成り立つので、
UNIQ386cc4f10a9e570-MathJax-934-QINU
極限(UNIQ386cc4f10a9e570-MathJax-935-QINU)をとれば、
UNIQ386cc4f10a9e570-MathJax-936-QINU
この左辺は極限の性質からUNIQ386cc4f10a9e570-MathJax-937-QINU に等しいので、
UNIQ386cc4f10a9e570-MathJax-938-QINU
命題6とその直後のUNIQ386cc4f10a9e570-MathJax-939-QINUの定義から、
UNIQ386cc4f10a9e570-MathJax-940-QINU
UNIQ386cc4f10a9e570-MathJax-941-QINU
UNIQ386cc4f10a9e570-MathJax-942-QINU
この3つの式を式(a)に代入すると、
UNIQ386cc4f10a9e570-MathJax-943-QINU
累乗規則の1が成り立つことが示せた。
対数と対数関数
1と異なる正の実数 UNIQ386cc4f10a9e570-MathJax-944-QINU を考える。
指数関数 UNIQ386cc4f10a9e570-MathJax-945-QINU は,定理2から、
UNIQ386cc4f10a9e570-MathJax-946-QINU から UNIQ386cc4f10a9e570-MathJax-947-QINU の上への、一対一、連続関数である。
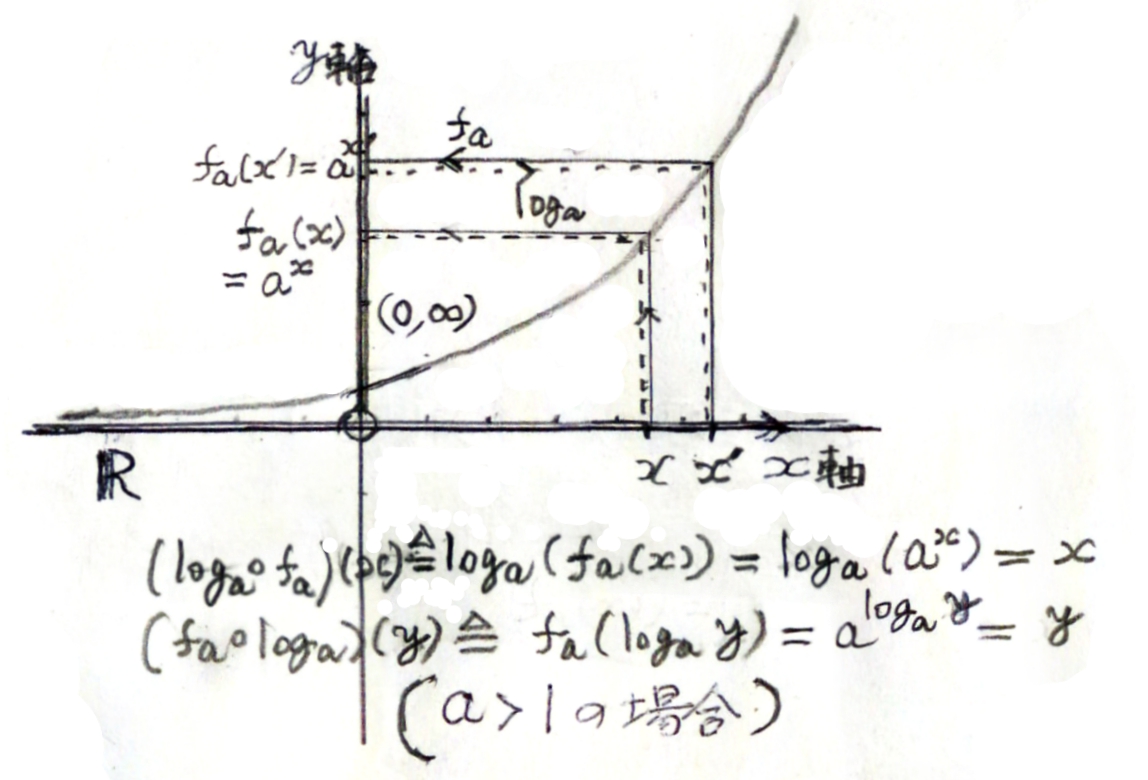
定義1
実数 UNIQ386cc4f10a9e570-MathJax-948-QINU を UNIQ386cc4f10a9e570-MathJax-949-QINU とする。この時、
任意の正の実数 Xに対して、
UNIQ386cc4f10a9e570-MathJax-950-QINU
を満たす実数xが唯一つ定まる。
このxを X のUNIQ386cc4f10a9e570-MathJax-951-QINU を底とする対数と呼び、UNIQ386cc4f10a9e570-MathJax-952-QINU とかく。
指数関数 UNIQ386cc4f10a9e570-MathJax-953-QINU は
UNIQ386cc4f10a9e570-MathJax-954-QINU から UNIQ386cc4f10a9e570-MathJax-955-QINU の上への、一対一関数
なので、逆関数を考えることができる。
定義2
UNIQ386cc4f10a9e570-MathJax-956-QINU を1と異なる正の実数とする。
UNIQ386cc4f10a9e570-MathJax-957-QINU
この関数を、UNIQ386cc4f10a9e570-MathJax-958-QINU を底とする対数関数とよぶ。
定理1
UNIQ386cc4f10a9e570-MathJax-959-QINU を 1と異なる正の実数とする。
1) UNIQ386cc4f10a9e570-MathJax-960-QINU を底とする対数関数 UNIQ386cc4f10a9e570-MathJax-961-QINU は、
指数関数UNIQ386cc4f10a9e570-MathJax-962-QINUの逆関数であり、
UNIQ386cc4f10a9e570-MathJax-963-QINU
すなわち、
UNIQ386cc4f10a9e570-MathJax-964-QINU
と(注参照)、
UNIQ386cc4f10a9e570-MathJax-965-QINU
すなわち、
UNIQ386cc4f10a9e570-MathJax-966-QINU
を満たす。
2)指数関数UNIQ386cc4f10a9e570-MathJax-967-QINU は
UNIQ386cc4f10a9e570-MathJax-968-QINU から UNIQ386cc4f10a9e570-MathJax-969-QINU の上への一対一で
連続な関数である。
(注) 2つの関数f、gに対して、その合成関数UNIQ386cc4f10a9e570-MathJax-970-QINU は、
UNIQ386cc4f10a9e570-MathJax-971-QINU で定義される。
定理2
UNIQ386cc4f10a9e570-MathJax-972-QINU を 1と異なる正の実数とする。
すると
1) 任意の2つの正の実数b、cに対して,
UNIQ386cc4f10a9e570-MathJax-973-QINU
2) 任意の2つの正の実数 b,c に対して,
UNIQ386cc4f10a9e570-MathJax-974-QINU
3) 任意の正の実数 b と任意の実数 c に対して
UNIQ386cc4f10a9e570-MathJax-975-QINU
証明
1) 指数関数UNIQ386cc4f10a9e570-MathJax-976-QINU の性質から、
UNIQ386cc4f10a9e570-MathJax-977-QINU
を満たす、実数 UNIQ386cc4f10a9e570-MathJax-978-QINU がそれぞれ唯一つ定まる。
式(7)から対数関数の定義を用いると、
UNIQ386cc4f10a9e570-MathJax-979-QINU
すると、
UNIQ386cc4f10a9e570-MathJax-980-QINU
UNIQ386cc4f10a9e570-MathJax-981-QINU
UNIQ386cc4f10a9e570-MathJax-982-QINU
UNIQ386cc4f10a9e570-MathJax-983-QINU
2)も同様に証明できる。
3)UNIQ386cc4f10a9e570-MathJax-984-QINU とおく。すると、対数の定義から、
UNIQ386cc4f10a9e570-MathJax-985-QINU
UNIQ386cc4f10a9e570-MathJax-986-QINU bは正の実数なので、UNIQ386cc4f10a9e570-MathJax-987-QINUなので、
UNIQ386cc4f10a9e570-MathJax-988-QINU
故に
UNIQ386cc4f10a9e570-MathJax-989-QINU
指数関数が一対一関数なので、UNIQ386cc4f10a9e570-MathJax-990-QINU
X の定義から、UNIQ386cc4f10a9e570-MathJax-991-QINU
定理3 底の変換公式
任意の3つの正の実数 UNIQ386cc4f10a9e570-MathJax-992-QINU に対して
UNIQ386cc4f10a9e570-MathJax-993-QINU
証明
定理1の式(3')から、
UNIQ386cc4f10a9e570-MathJax-994-QINU
底をcとする対数をとれば、
UNIQ386cc4f10a9e570-MathJax-995-QINU
UNIQ386cc4f10a9e570-MathJax-996-QINU定理2の式(6)から、UNIQ386cc4f10a9e570-MathJax-997-QINUなので、
UNIQ386cc4f10a9e570-MathJax-998-QINU
UNIQ386cc4f10a9e570-MathJax-999-QINU は、1と異なる正の実数であるため、UNIQ386cc4f10a9e570-MathJax-1000-QINU となり、
UNIQ386cc4f10a9e570-MathJax-1001-QINU
が得られた。
証明終わり。 UNIQ386cc4f10a9e570-MathJax-1002-QINU
対数関数
1と異なる正の実数 UNIQ386cc4f10a9e570-MathJax-1003-QINU を考える。
指数関数 UNIQ386cc4f10a9e570-MathJax-1004-QINU は,定理2から、
UNIQ386cc4f10a9e570-MathJax-1005-QINU から UNIQ386cc4f10a9e570-MathJax-1006-QINU の上への、一対一、連続関数である。
すると、その逆関数UNIQ386cc4f10a9e570-MathJax-1007-QINU が定義できる。
定義
UNIQ386cc4f10a9e570-MathJax-1008-QINU を1と異なる正の実数とする。
UNIQ386cc4f10a9e570-MathJax-1009-QINU
この関数を、UNIQ386cc4f10a9e570-MathJax-1010-QINU を底とする対数関数とよぶ。
定理1
UNIQ386cc4f10a9e570-MathJax-1011-QINU を 1と異なる正の実数とする。
1) UNIQ386cc4f10a9e570-MathJax-1012-QINU を底とする対数関数 UNIQ386cc4f10a9e570-MathJax-1013-QINU は、
指数関数UNIQ386cc4f10a9e570-MathJax-1014-QINUの逆関数であり、
UNIQ386cc4f10a9e570-MathJax-1015-QINU
すなわち、
UNIQ386cc4f10a9e570-MathJax-1016-QINU
と(注参照)、
UNIQ386cc4f10a9e570-MathJax-1017-QINU
すなわち、
UNIQ386cc4f10a9e570-MathJax-1018-QINU
を満たす。
2)指数関数UNIQ386cc4f10a9e570-MathJax-1019-QINU は
UNIQ386cc4f10a9e570-MathJax-1020-QINU から UNIQ386cc4f10a9e570-MathJax-1021-QINU の上への一対一で
連続な関数である。
(注) 2つの関数f、gに対して、その合成関数UNIQ386cc4f10a9e570-MathJax-1022-QINU は、
UNIQ386cc4f10a9e570-MathJax-1023-QINU で定義される。
定理2
UNIQ386cc4f10a9e570-MathJax-1024-QINU を 1と異なる正の実数とする。
すると
1) 任意の2つの正の実数b、cに対して,
UNIQ386cc4f10a9e570-MathJax-1025-QINU
2) 任意の2つの正の実数 b,c に対して,
UNIQ386cc4f10a9e570-MathJax-1026-QINU
3) 任意の正の実数 b と任意の実数 c に対して
UNIQ386cc4f10a9e570-MathJax-1027-QINU
証明
1) 指数関数UNIQ386cc4f10a9e570-MathJax-1028-QINU の性質から、
UNIQ386cc4f10a9e570-MathJax-1029-QINU
を満たす、実数 UNIQ386cc4f10a9e570-MathJax-1030-QINU がそれぞれ唯一つ定まる。
式(7)から対数関数の定義を用いると、
UNIQ386cc4f10a9e570-MathJax-1031-QINU
すると、
UNIQ386cc4f10a9e570-MathJax-1032-QINU
UNIQ386cc4f10a9e570-MathJax-1033-QINU
UNIQ386cc4f10a9e570-MathJax-1034-QINU
UNIQ386cc4f10a9e570-MathJax-1035-QINU
2)も同様に証明できる。
3)UNIQ386cc4f10a9e570-MathJax-1036-QINU とおく。すると、対数の定義から、
UNIQ386cc4f10a9e570-MathJax-1037-QINU
UNIQ386cc4f10a9e570-MathJax-1038-QINU bは正の実数なので、UNIQ386cc4f10a9e570-MathJax-1039-QINUなので、
UNIQ386cc4f10a9e570-MathJax-1040-QINU
故に
UNIQ386cc4f10a9e570-MathJax-1041-QINU
指数関数が一対一関数なので、UNIQ386cc4f10a9e570-MathJax-1042-QINU
X の定義から、UNIQ386cc4f10a9e570-MathJax-1043-QINU
定理3 底の変換公式
任意の3つの正の実数 UNIQ386cc4f10a9e570-MathJax-1044-QINU に対して
UNIQ386cc4f10a9e570-MathJax-1045-QINU
証明
定理1の式(3')から、
UNIQ386cc4f10a9e570-MathJax-1046-QINU
底をcとする対数をとれば、
UNIQ386cc4f10a9e570-MathJax-1047-QINU
UNIQ386cc4f10a9e570-MathJax-1048-QINU定理2の式(6)から、UNIQ386cc4f10a9e570-MathJax-1049-QINUなので、
UNIQ386cc4f10a9e570-MathJax-1050-QINU
UNIQ386cc4f10a9e570-MathJax-1051-QINU は、1と異なる正の実数であるため、UNIQ386cc4f10a9e570-MathJax-1052-QINU となり、
UNIQ386cc4f10a9e570-MathJax-1053-QINU
が得られた。
証明終わり。 UNIQ386cc4f10a9e570-MathJax-1054-QINU